各格特征及实践中的意义

2023-11-08 理论教育版权反馈

【摘要】：上面是说明第一格三段论式的特征皆有其故可得的。第一格的意义：第一格亚里斯多德称之为完全格[17]，其原因有四：其一，在第一格能得出A、E、I、O 四种类型的结论，为其他各格所不能的，因为A 型结论只在第一格才能得出。由上所论证，可见第三格的特征都是根据三段论式的一般规则的。

（1）第一格：有四个合乎规定的式，如上述。

从这四个式可以看出：

（a）大前提都是全称命题。

（b）小前提都是肯定命题。

（c）结论的质与大前提的质相同，其量则与小前提的量相同。

为什么是这样的结论？

大前提都是全称，因为如果大前提是特称，则其主词M 不周延，则M在小前提必须周延，然后才有得出结论的条件，而M 在小前提是宾词，如要周延，则小前提必须是否定的，那么，结论又必是否定的，则P必须在大前提周延，那就须大前提也是否定的，而小前提既已是否定的，那就会有两个否定的前提，便不能得出结论，故大前提不能是特称的，而必须是全称的。

小前提必须是肯定的，如果它是否定的，则结论必是否定的，则P 必须在大前提周延，则大前提亦必否定，而小前提既已否定，那就是两前提皆否定，无结论得出之可能。故小前提不能是否定的，它必须是肯定的。

结论之量同于小前提之量，因小前提的主词是S，所以视乎S在小前提是否周延而定其在结论之是否周延，故结论之量与小前提之量相同。结论之质与大前提之质相同，因为第一格的特征之一乃是其小前提必是肯定的，如上所证明，那么，如果大前提又是肯定的，则两前提皆肯定则结论是肯定的；如果大前提是否定的，则两前提中有一个是否定的，其结论必否定。可见结论之质是和大前提的质相同的，原因乃是小前提必是肯定的。

上面是说明第一格三段论式的特征皆有其故可得的。第一格的意义：

（a）第一格亚里斯多德称之为完全格^[17]，其原因有四：其一，在第一格能得出A、E、I、O 四种类型的结论，为其他各格所不能的，因为A 型结论只在第一格才能得出。其二，如亚里斯多德所说，“一个三段论式在其陈说之外，不须另外什么来明白地得出其结论的，称为完全格；不完全格必须在其前提所说之外至少有一个命题，纵然这命题是原有前提的后果，然后才能得出结论”^[18]。所说的前提之外另一个命题是指变格中所用的换位，详见后文变格的第一节。其三，一般人都认为第一格的思路是自然的：其大前提的宾词就是结论的宾词，其小前提的主词就是结论的主词。其四，大前提是全称的一个命题，得出一个原则，M 是或不是P，而小前提肯定S是属于M 的，所以P是怎样说到M，根据三段论式的公理，P也同样地说到S，因之第一格最直接地显示这公理的应用。

（b）第一格的形式是演绎科学的形式，先举出一条原则，再举其一定的事例，然后把原则应用在这事例上面。法院判决是应用这方式的。

（2）第二格：有四个合乎规定的式，如上述。

从这四个式可以看出：

（a）前提之一必为否定。

（b）大前提必为全称。

（c）结论必为否定。

为什么是这样的呢？

第二格里面，中词M 在两前提中都是宾词，而M 在前提中必须至少周延一次。那就是说，两前提中有一个（而只一个，但不管是哪一个）是否定的，以使M 能周延，故前提之一必为否定。

既有一前提是否定，则按三段论式的规则，结论必是否定的，则P 在结论中必周延，故在大前提亦须周延，而P 在大前提是主词，只有大前提是一个全称命题，才能使P周延。

故第二格的大前提必是全称的。

其结论必为否定，已经说明，兹不重复。

可见第二格的特征都是有其理由的。

第二格的意义：

（a）大词P在前提中是主词而在结论中是宾词，这是颠倒的秩序，亚里斯多德认为这是不自然的。

（b）第二格的结论都是否定的，非E 即O，论证此物，或此一类事物，或有些这类的事物不是什么，故最宜于反驳论敌的全称肯定论题。论敌的A 型论题，我们可以E来推翻，亦可以O 来推翻，但成立O 比较易，而成立E则比较难，O 固然是够来达到推翻A 的目的，可是如果能成立E，其说服力则更大。

（3）第三格：有六个合乎规定的式，如上述。

从这六个式可以看出：

（a）小前提都是肯定的。

（b）结论都是特称的。

为什么是这样的呢？(www.chuimin.cn)

第三格的小前提必须是肯定的，因为如果小前提是否定的，则结论必须是否定的，则P在结论周延，而在大前提就必须周延，但P在第三格是大前提的宾词，如要它周延，则大前提必须否定，今假定小前提是否定的，就会有两个否定前提，那就得不出结论，故小前提为否定的这种假定是不可能的，证明第三格的小前提必须是肯定的。

结论必是特称的，因为第三格的小前提已经证明，必须是肯定的，而S是这肯定前提的宾词，所以在前提中是未周延的，因之它在结论中不得周延，所以结论是特称的。

由上所论证，可见第三格的特征都是根据三段论式的一般规则的。

第三格的意义：

（a）第三格的S在前提中是宾词而在结论中是主词，这是秩序的颠倒。以前提的宾词为结论的主词，在思想上有些不自然的。

（b）第三格的结论都是特称的，不是I就是O，而I是E 的矛盾，O 是A 的矛盾；证明I便是指出E 的例外而就推翻了E，证明O 便是指出A的例外而就推翻了A。所以第三格是最适宜于攻破论敌所作的全称肯定或全称否定的论点是指出例外的论证方式。

（c）第三格两前提的主词都是M，而它的六个式中三个式是，M 是P而M 又是S的形式。S和P是不同的东西，用来陈述M 的，可能无法成立它们之间的关系，但通过M 便证明有些S是P。

（4）第四格：有五个合乎规定的式，如上述。

从这五个式可以看出：

（a）结论的形式有E、I、O 三种，前提AA 得I的结论，而前提AE 得E的结论，前提EA 却得O 的结论，情形看来是比较复杂的，不易看出其规律性，因之有些逻辑家认为实际上很可不必用第四格，而且只要把这格的大小前提倒置过来，就变成了第一格，只是变成第一格之后，其结论的主词是P，把所得的结论加以换位，便得到以S为主词的结论了。

例如第四格的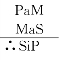 pagenumber_ebook=207,pagenumber_book=191 ，如将大小前提倒置，便成为第一格的，以这结论换位之后，便得SiP，即原来第四格的结论。

但是，虽然如此，我们却不应该不考虑第四格，因为如果以M 在两前提中的位置来决定三段论式的格时，没有第四格是会使系统不完整的。

第四格亦有其特征可言的：看它的五个式，不只是使我们有着上述的观感，仔细看来，还有下面的几点。

（b）如果前提有一个是否定，则大前提必须全称（大前提是全称否定，便合此条件）。

（c）如果大前提是肯定，则小前提必须全称。

（d）如果小前提是肯定，则结论必须是特称。

（e）大小前提皆无特称否定的。

（f）结论没有A 型命题的。

上面之所谓特征几点，大都是可以明显地看出根据三段论式一般规则得出的结果，其不是十分明显的，一经指出，亦不难理解的。

例如，如果前提有一个是否定的，则结论必是否定的，则P是周延的，因之在前提中也得要周延，而P 在大前提中是主词，所以大前提必须全称，否则犯大词非法周延的错误。

又如，如果大前提是肯定，则M 在大前作为肯定命题的宾词是未周延的，所以小前提必须全称才能使它的主词M 得到周延，否则犯中词未周延的错误。

又如，如果小前提是肯定，则其宾词S未周延，故结论必须是特称的。

大小前提皆无特称否定的这一点，是需要加以论证的，但也不过是三段论式一般规则的应用。因为如果有一前提是特称否定（O），它首先不能够作为大前提；如果大前提是否定，则结论必是否定，则P 须得要在大前提中周延，但我们在这里假定大前提是O，所以P 是未周延的，O 也不能作为小前提，因为如果小前提是MoS，则M 在这里未周延，就须在大前提周延，而M 在大前提是宾词，故大前提要使M 周延，就必须是一个否定命题，但小前提已经假定是O，这就会有两个否定的前提，便无结论，可见大小前提都不能是O。

第四格不能有A 型命题以表达其结论，因为如果要得出A 的结论，S必须在小前提周延，但S在小前提是宾词，要周延，则小前提必须是一个否定的命题，可是有了一个否定的前提，则结论必是否定的，便不能是A。可见A 不能作为第四格三段论式的结论。

上面是说明第四格的特征，都是从三段论式一般规则推演出来的。

第四格的意义：

（a）第四格S有前提中是宾词而在结论中是主词，P在前提中是主词而在结论中是宾词，顺序很不自然的，但是在亚里斯多德的三段论式中没有第四格，其原因都不是在此^[19]。亚氏的格不完全依中词在前提中的地位，而主要是依中词与大小词之外延大小而决定，没有我们现在的第四格是有其一定的理由的。

（b）第四格的结论都可将第四格改变为第一格而得出，所以从这点讲来，第四格没有它的特殊实践意义。但我们为完整格的系统起见，仍然保存着这第四格，而有时也用得着它的。况且近两千年来，形式逻辑的三段论式都沿用第四格，没有严重的理由要将它废掉。

注意：我们在上面简单地讨论了三段论式的公理、规则、格与式。其实这一切连同上章所讲的判断变形、逻辑正方形上的判断间的关系，都可用图解作直观的说明，并不必去管上面所讲的规则，也不必去问三段论式的格与式。任何一个三段论式的正确与否都可用图解来检查出来的。为着适合教学，我们不把这套图解编入本书的正文，而把它列为附录六，以供参考，亦可作为教学与学习的补充资料，三段论式的图解详见该附录六的第三部分。

各格特征及实践中的意义

相关推荐