从频繁项目集中生成所有可信关联规则，置信度大于minconf的规则为可信关联规则。C3：｛柴胡，黄芩，清半夏｝：2F3：｛柴胡，黄芩，清半夏｝：23.Apriori算法流程4.候选项集生成算法候选项集生成算法根据长度为k-1的频繁项目集Fk-1，经过两个步骤生成长度为k的候选项集Ck。......
2023-11-08
KMeans算法在医药领域的应用
【摘要】：KMeans可能由于初始值选择的不同，导致最终的结果不同。图4-4KMeans算法迭代过程假设对于相同的样本数据，若随机选择的两个初始点为序号4和7。对于同一个数据集，由于KMeans算法对初始选取的聚类中心敏感，因此可用该准则评价聚类结果的优劣。通常，对于任意一个数据集，KMeans算法无法达到全局最优，只能达到局部最优。
1.KMeans算法简介
给定n个样本的数据集以及要生成的簇的数目k，划分方法将样本组织为k个划分（k≤n），每个划分代表一个簇。
划分准则：同一个簇中的样本尽可能接近或相似，不同簇中的样本尽可能远离或不相似，以样本间的距离作为相似性度量。
典型的划分方法：KMeans（k-均值），由簇中样本的平均值来代表整个簇。kmedoids（k-中心点），由处于簇中心区域的某个样本代表整个簇，KMeans算法示例如图4-3所示。
簇不再发生变化或准则函数收敛。平方误差准则，P是空间中的点，mi是簇Ci的平均值：
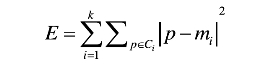
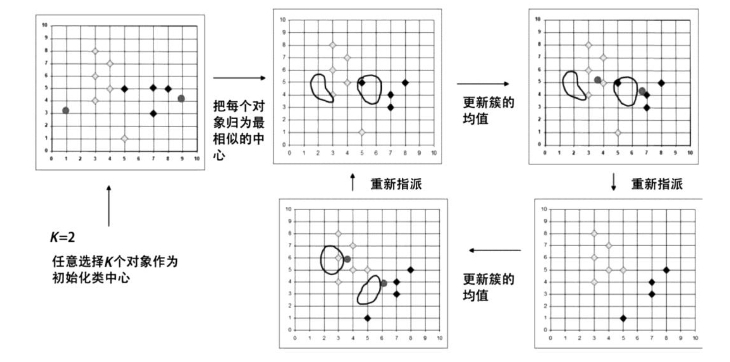
图4-3 KMeans算法示例
由图4-3可以看出，KMeans的基本算法是很容易理解的，算法本身也简单，运行较快，所以，KMeans可用于非常大型的数据集。但是，KMeans也有一些缺点：
（1）对初始值敏感。KMeans可能由于初始值选择的不同，导致最终的结果不同。scikit-learn里面KMeans算法的参数中有个“init”参数，将其设置成“init=KMeans++”，可以在初始化均值向量的时候让它们之间尽量分开。
（2）对特殊分布的数据集不能够得出合理的结果。
2.KMeans算法示例
Kmeans算法示例数据如表4-9所示。
表4-9 KMeans算法示例数据
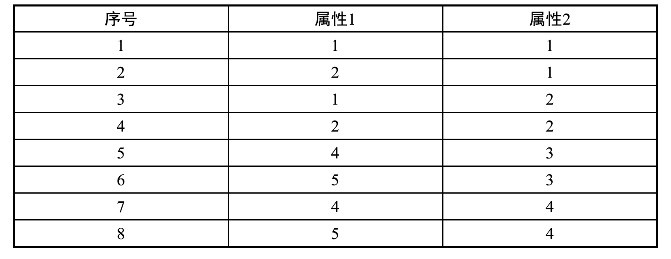
根据所给的数据通过对其实施KMeans（设n=8，k==2），其主要执行以下步骤：
第一次迭代：假定随机选择的两个对象，如将序号1和序号3当作初始点，分别找到离两点最近的对象，并产生两个簇｛1，2｝和｛3，4，5，6，7，8｝。
对于产生的簇分别计算平均值，得到平均值点。
对于｛1，2｝，平均值点为（1.5，1）；
对于｛3，4，5，6，7，8｝，平均值点为（3.5，3）。(www.chuimin.cn)
第二次迭代：通过平均值调整对象所在的簇，重新聚类，即将所有点按离平均值点（1.5，1）（3.5，3）最近的原则重新分配。得到两个新的簇：｛1，2，3，4｝和｛5，6，7，8｝。重新计算簇平均值点，得到新的平均值点为（1.5，1.5）和（4.5，3.5）。
第三次迭代：将所有点按离平均值点（1.5，1.5）和（4.5，3.5）最近的原则重新分配，调整对象，簇仍然为｛1，2，3，4｝和｛5，6，7，8｝，发现没有出现重新分配，而且准则函数收敛，程序结束。
KMeans算法迭代过程如图4-4所示。
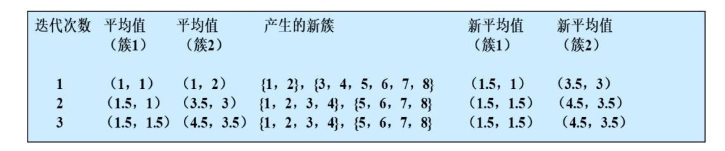
图4-4 KMeans算法迭代过程
假设对于相同的样本数据，若随机选择的两个初始点为序号4和7。
问题1：结果与前面会一样吗？
问题2：有何结论？
KMeans算法的评价准则：误差平方和准则。
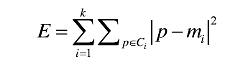
误差平方和达到最优（小）时，可以使各聚类的类内尽可能紧凑，而使各聚类之间尽可能分开。
对于同一个数据集，由于KMeans算法对初始选取的聚类中心敏感，因此可用该准则评价聚类结果的优劣。
通常，对于任意一个数据集，KMeans算法无法达到全局最优，只能达到局部最优。
3.KMeans算法优缺点
优点：可扩展性较好，算法复杂度为0（nkt）。其中：n为样本个数，k是簇的个数，t是迭代次数。
缺点：簇数目k需要事先给定，但非常难以选定；初始聚类中心的选择对聚类结果有较大的影响；不适合于发现非球状簇；对噪声和离群点数据敏感。
图4-5 KMeans算法初始聚类中心的选择
4.KMeans方法的变种
有许多KMeans算法的变种，区别在于初始k个平均值的选择、相异度的计算、计算聚类平均值的策略。例如处理分类数据，k-众数方法，用众数代替簇的平均值；采用新的相异度度量；采用基于频率的方法更新簇众数；混合处理分类和数值数据：k-原型方法（k-prototype）；将k-均值和k-众数方法综合起来。K-Medoids：用中心点（位于簇最中心位置的对象）而不是簇中对象的平均值作为参考点。
有关大数据挖掘技术及其在医药领域的应用的文章
- 详细阅读
-
决策树分类算法在医药领域的应用详细阅读
决策树可以用来对未知样本进行分类。决策树分类算法使用场景，这个监督式学习算法通常被用于分类问题，它同时适用于分类变量和连续因变量。信息增益是决策树常用的分枝准则，在树的每个结点上选择具有最高信息增益的属性作为当前结点的划分属性。......
2023-11-08
-
CART分类算法在医药领域的应用详细阅读
随机森林是通过将很多的决策树组合而成的，随机森林采用CART算法。另外，针对CART的分类树和回归树，它们的计算方法有所不同，数值型和分类型属性变量的计算方法也存在差异。CART算法使用Gini系数来度量对某个属性变量测试输出的两组取值的差异性。表3-8C4.5算法和CART算法比较......
2023-11-08
-
C4.5分类算法在医药领域的应用详细阅读
在C4.5算法中采用概率的方法，为缺失值的每个可能值赋予一个概率，而不是简单地用最常见的值替代该缺失值。C4.5决策树的生长阶段算法伪代码：C4.5决策树的剪枝处理阶段算法伪代码：5.C4.5算法的优缺点与其他分类算法相比，C4.5分类算法具有如下优点：产生的分类规则易于理解，准确率较高。为适应大规模数据集，在C4.5后出现有SLIQ和SPRINT等算法。......
2023-11-08
-
聚类分析算法及应用-大数据挖掘技术在医药领域详细阅读
聚类分析的算法可以分为划分的方法、层次的方法、基于密度的方法、基于网格的方法、基于模型的方法等，其中，前两种方法最常用。图4-6层次聚类法示例4.基于网格的方法基于网格的聚类方法采用一个网格数据结构，把对象空间量化为有限数目的单元，形成了一个网格结构。......
2023-11-08
-
大数据挖掘在医药领域的应用详细阅读
数据挖掘就是从大量的、不完全的、有噪声的、模糊的、随机的数据中，提取隐含在其中的、人们事先不知道的、但又是潜在有用的信息和知识的过程。数据挖掘的替换词，包括数据库中的知识挖掘、知识提炼、数据/模式分析、数据考古、数据捕捞、信息收获，等等。数据挖掘方面更多的国际会议，如PAKDD，PKDD，SIAM-Data Mining，ICDM，DaWaK，SPIE-DM等。......
2023-11-08
-
HBaseShell:在医药领域的大数据挖掘详细阅读
在HBase Shell提示符下执行help命令可列出所有命令列表。命名空间类命令命名空间是对表的逻辑分组，HBase可以针对命名空间分配资源限额，指定HRegionServer子集，进行安全管理等。大多数配置更改后必须重新启动HBase集群才能生效，与HRegion压缩、拆分相关的参数可以动态更改，更改后在HBase Shell中执行update_all_config命令即可生效。......
2023-11-08
-
大数据挖掘技术在医药领域的应用详细阅读
打开VMware Workstation→点击文件→新建虚拟机。图9-2选择典型（推荐）选择“安装程序光盘映像文件”，选择指定的CentOS系统的.iso文件，点击“下一步〉”。图9-10在CentOS 6中安装VMware Tools重启CentOs 6。图9-11CentOS 6重启输入密码zkpk，登录进系统。图9-12CentOS 6安装完成下面克隆HadoopSlave。图9-14设置克隆虚拟机选项创建完整克隆。图9-16命名虚拟机图9-17正在准备克隆虚拟机图9-18正在克隆虚拟机点击“关闭”按钮后，发现“HadoopSlave”虚拟机已经在左侧的列表栏中。......
2023-11-08
相关推荐