数据挖掘就是从大量的、不完全的、有噪声的、模糊的、随机的数据中，提取隐含在其中的、人们事先不知道的、但又是潜在有用的信息和知识的过程。数据挖掘的替换词，包括数据库中的知识挖掘、知识提炼、数据/模式分析、数据考古、数据捕捞、信息收获，等等。数据挖掘方面更多的国际会议，如PAKDD，PKDD，SIAM-Data Mining，ICDM，DaWaK，SPIE-DM等。......
2025-09-30
4种相似度计算方法-大数据挖掘技术及其在医药领域的应用
【摘要】：例：已知两个样本p=［1000000000］和q=［0000001001］4.多值离散型属性的相似性计算方法多值离散型属性是指取值个数大于2的离散型属性。
1.相似度计算方法
样本之间的相似性通常采用样本之间的距离来表示：两个样本之间的距离越大，表示两个样本越不相似，差异性越大；两个样本之间的距离越小，表示两个样本越相似，差异性越小。特例：当两个样本之间的距离为零时，表示两个样本完全一样，无差异。
样本之间的距离是在样本的描述属性（特征）上进行计算的：连续型属性（如重量、高度、年龄等），二值离散型属性（如性别、考试是否通过等），多值离散型属性（如收入分为高、中、低等），混合类型属性（上述类型的属性至少同时存在两种）。
2.连续型属性的相似性计算方法
令Xi=（xi1，xi2，…，xid）是第i个样本观察值，Xj=（xj1，xj2，…，xjd）是第j个样本观察值，它们都是d维的特征向量，并且每维特征都是一个连续型数值。那么，样本Xi和Xi之间的各种距离：
欧氏距离（Euclidean Distance）：
曼哈顿距离（Manhattan Distance）：
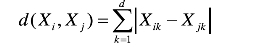
闵可夫斯基距离（Minkowski Distance）：
Euclidean距离和Manhattan距离的性质：
d（i，j）=0
d（i，i）=0
d（i，j）=d（j，i）
d（i，j）=d（i，k）+d（k，j）
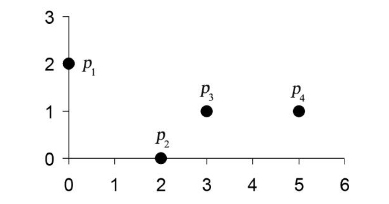
图4-2 相似性计算示例之平面图
表4-3 相似性计算示例之坐标数据
表4-4 欧氏距离的示例
表4-5 曼哈顿距离的示例
3.二值离散型属性的相似性计算方法
二值离散型属性只有0和1两个取值。其中，0表示该属性为空，1表示该属性存在。
例如，描述病人是否抽烟的属性（Smoker），取值为1表示病人抽烟，取值为0表示病人不抽烟。
假设两个样本Xi和Xj分别表示成如下形式：
Xi=（xi1，xi2，…，xip）
Xj=（xj1，xj2，…，xjp）
它们都是p维的特征向量，并且每维特征都是一个二值离散型数值。
假设二值离散型属性的两个取值具有相同的权重，则可以得到一个两行两列的可能性矩阵。
表4-6 二值离散型属性的相似性计算方法示例
如果样本的属性都是对称的二值离散型属性，则样本间的距离可用简单匹配系数（Simple Matching Coefficients，SMC）计算：
SMC=（b+c）/（a+b+c+d）
其中，对称的二值离散型属性是指属性取值为1或者0同等重要。
例如，性别就是一个对称的二值离散型属性，即用1表示男性，用0表示女性；或者用0表示男性，用1表示女性是等价的，属性的两个取值没有主次之分。
如果样本的属性都是不对称的二值离散型属性，则样本间的距离可用Jaccard系数计算（Jaccard Coefficients，JC）：(https://www.chuimin.cn)
JC=（b+c）/（a+b+c）
其中，不对称的二值离散型属性是指属性取值为1或者0不是同等重要。
例如，血液的检查结果是不对称的二值离散型属性，阳性结果的重要程度高于阴性结果，因此通常用1来表示阳性结果，而用0来表示阴性结果。
例：已知两个样本p=［1000000000］和q=［0000001001］
4.多值离散型属性的相似性计算方法
多值离散型属性是指取值个数大于2的离散型属性。
例如，成绩可以分为优、良、中、差。
假设一个多值离散型属性的取值个数为N，给定数据集X=｛xi|i=1，2，…，total｝。
其中，每个样本Xi可用一个d维特征向量描述，并且每维特征都是一个多值离散型属性，即Xi=（xi1，xi2，…，xid）。
问题：给定两个样本Xi=（xi1，xi2，…，xid）和xj=（xj1，xj2，...，xjd），如何计算它们之间的距离？
方法一：简单匹配方法。
距离计算公式如下：
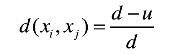
其中，d为数据集中的属性个数，u为样本xi和xj取值相同的属性个数。
表4-7 多值离散型属性的相似性计算示例数据
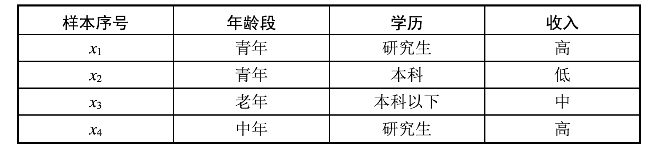
d（x1，x2）=（3-1）/3≈0.667
d（x1，x3）=（3-0）/3=1
d（x1，x4）=（3-2）/3≈0.333
方法二：先将多值离散型属性转换成多个二值离散型属性，然后再使用Jaccard系数计算样本之间的距离。
对有N个取值的多值离散型属性，可依据该属性的每种取值分别创建一个新的二值离散型属性，这样可将多值离散型属性转换成多个二值离散型属性。
表4-8 多值离散型属性的相似性计算结果
5.混合类型属性的相似性计算方法
问题：对于包含混合类型属性的数据集，如何计算样本之间的相似性？
方法：将混合类型属性放在一起处理，进行一次聚类分析。
假设：给定的数据集X=｛xi|i=1，2，…，total｝，每个样本用d个描述属性A1，A2，…，Ad来表示，属性Aj（1≤j≤d）包含多种类型。
在聚类之前，对样本的属性值进行预处理：对连续型属性，将其各种取值进行规范化处理，使得属性值规范化到区间［0.0，1.0］；对多值离散型属性，根据属性的每种取值将其转换成多个二值离散型属性。预处理之后，样本中只包含连续型属性和二值离散型属性。
给定两个样本xi=（xi1，xi2，…，xid）和xj=（xj1，xj2，...，xjd），它们之间的距离：
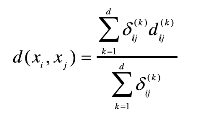
其中，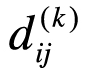
表示x和ix在j第k个属性上的距离。
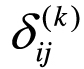表示第k个属性对计算x和x距j离的影响。
当第k个属性为连续型时，使用如下公式来计算
：
当第k个属性为二值离散型时，如果xik=xjk，则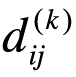
=0；否则，
=1。
表示第k个属性对计算x和ix距j离的影响。（1）如果xik或xjk缺失（即样本x或i样本x没j有第k个属性的度量值），则
=0。（2）如果xik=xjk=0，且第k个属性是不对称的二值离散型，则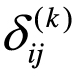
=0。（3）除了上述（1）和（2）之外的其他情况下，则
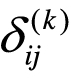=1。
相关文章
- 详细阅读
-
分类模型评价方法-大数据挖掘技术及其在医药领详细阅读
关于分类和回归模型的各种评估方法，一种是处理分类任务的模型，一种是预测回归的模型，这两种模型的评估方法也不完全一致，下面就来分别介绍两种类型模型的各种评估手段。AUC可以说是用单个数字总结模型性能的最好方法，其实就是ROC曲线下方的面积大小。平均绝对误差可以避免误差相互抵消的问题，因而可以准确反映实际预测误差的大小。MAE可以表示预测与实际结果的接近程度。以上即为两种模型的常用评估方法。......
2025-09-30
-
医药领域的大数据挖掘技术及应用详细阅读
医疗数据类型的多样化，包括数值型数据、类别型数据、图像、文字、信号、语音、视频。高科技的医学检查设备每天都会产生数千兆字节数据。数学特征不显著。数据归属权问题、数据安全问题、法律诉讼问题等。图1-6医疗数据可及性医学数据类型及特点主要包括多系统多类型、数据量大、增量迅速、结构复杂。绝大多数的医疗数据是处于归档状态，检索是十分复杂的。缺乏数据标准，导致无法统一。......
2025-09-30
-
大数据挖掘技术在医药领域中的贝叶斯公式应用详细阅读
，n），则3.贝叶斯定理贝叶斯，在《An Essay towards solving a Problem in the Doctrine of Chances》中给出了贝叶斯定理。其基本求解公式：贝叶斯公式：P（B|A）是根据A判断其属于类别B的概率，称为后验概率。......
2025-09-30
-
大数据挖掘在医药领域的应用及功能详细阅读
数据挖掘的功能是指数据挖掘通过预测未来趋势及行为，做出前瞻的、基于知识的决策。数据挖掘的任务主要是关联分析、聚类分析、分类、预测、时间序列模式和偏差分析等。关联分析的目的是找出数据库中隐藏的关联网。关联分析发现关联规则，这些规则展示属性值频繁地在给定数据集中一起出现的条件。聚类分析可以建立宏观的概念，发现数据的分布模式以及可能的数据属性之间的相互关系。......
2025-09-30
-
大数据挖掘技术在医药领域的内容与特点详细阅读
机器学习算法从数据中自动分析获得规律，并利用规律对未知数据进行预测。数据挖掘与传统联机分析处理OLAP不同，对大数据的深度分析主要基于大规模的机器学习技术。图1-11数据挖掘与机器学习......
2025-09-30
-
医药领域大数据挖掘技术的关联规则挖掘详细阅读
关联规则是寻找在同一个事件中出现的不同项的相关性。关联分析即利用关联规则进行数据挖掘。关联规则挖掘问题的描述：项目集，设I=｛i1，i2，…关联规则挖掘的目标，给定一个事务集合T，关联规则挖掘即找出T中所有满足支持度和置信度分别高于一个用户指定的最小支持度和最小置信度的关联规则。......
2025-09-30
-
大数据挖掘技术在医药领域中的数据库与数据仓库详细阅读
数据库由数据库管理系统统一管理，数据的插入、修改和检索均要通过数据库管理系统进行。软件主要包括操作系统、各种宿主语言、实用程序以及数据库管理系统。数据库管理系统是一种系统软件，它的主要功能是维护数据库并有效地访问数据库中任意部分数据。对数据库的维护包括保持数据的完整性、一致性和安全性。数据仓库的多维特征满足以多维数据为核心的多维数据分析。......
2025-09-30
相关推荐