医药数据聚类分析：大数据挖掘应用

2023-11-08 理论教育版权反馈

【摘要】：表4-2某大型医院三年住院治疗情况（续表）医学图像数据聚类分析。中医药数据聚类分析。图4-1聚类数据示例聚类分析在数据挖掘中的作用：作为一个独立的工具来获得数据集中数据的分布情况。Q型聚类分析是对样本进行分类处理。根据变量的分类结果以及它们之间的关系，可以选择主要变量进行回归分析或Q型聚类分析。

1.聚类分析在医药领域的应用

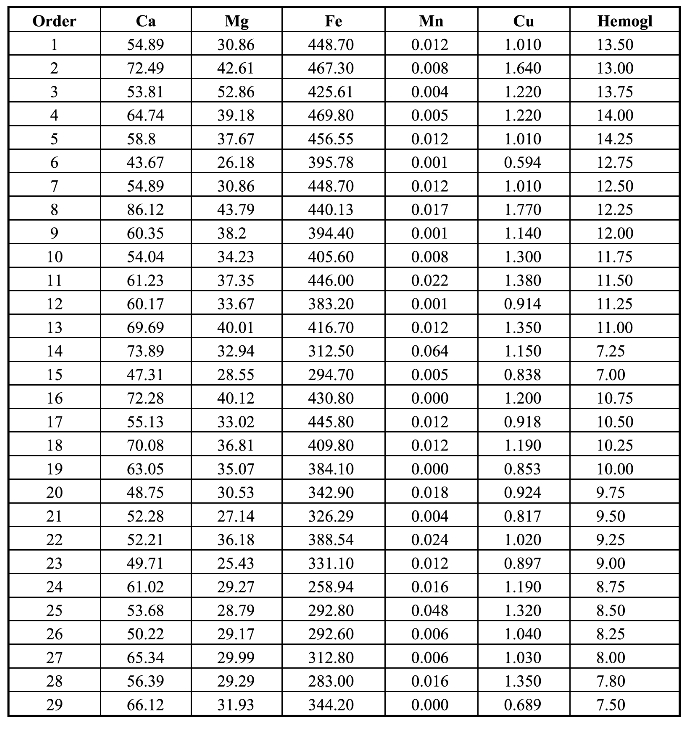
聚类分析（Cluster Analysis）是根据事物本身的特性研究个体分类的方法，其原则是同一类中的个体有较大的相似性，不同类的个体差别比较大。根据分类对象的不同分为样品聚类和变量聚类。例如，已知29例儿童的血中血红蛋白、钙、镁、铁、锰、铜的含量如表4-1所示，试对数据进行变量聚类分析。

表4-1　儿童血红蛋白浓度与血中金属元素的数据集

pagenumber_ebook=137,pagenumber_book=126

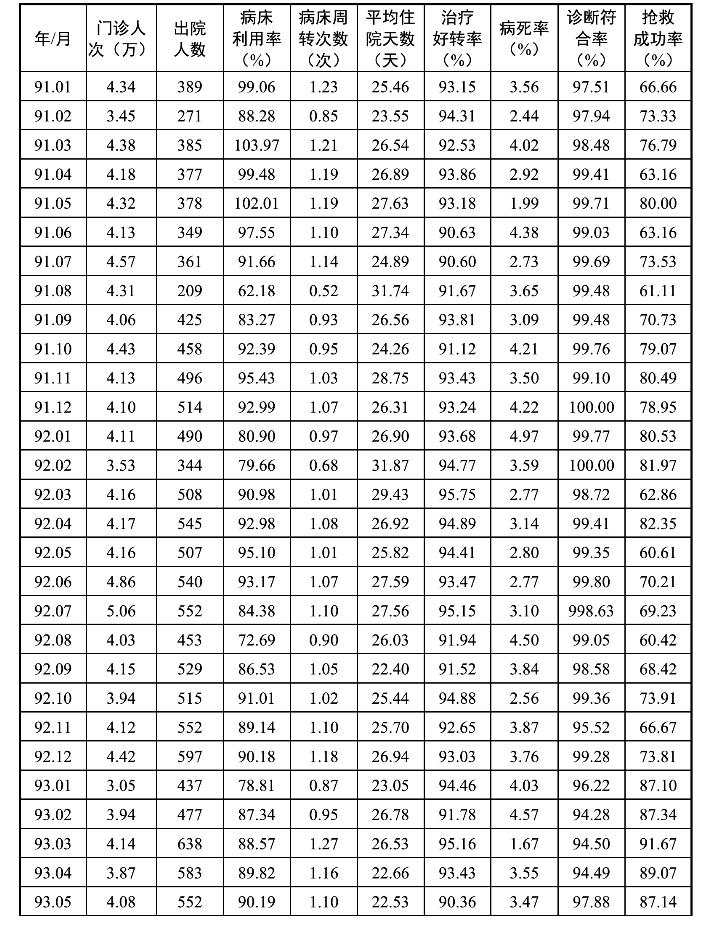
了解某三甲医院住院医疗质量情况及其特征，为医院医疗质量精细化管理提供决策依据。选取反映医疗质量的多项指标，采用聚类分析法分析医疗质量特征，针对不同特征采取相应改进措施，可推动医院管理的标准化、专业化和精细化建设。

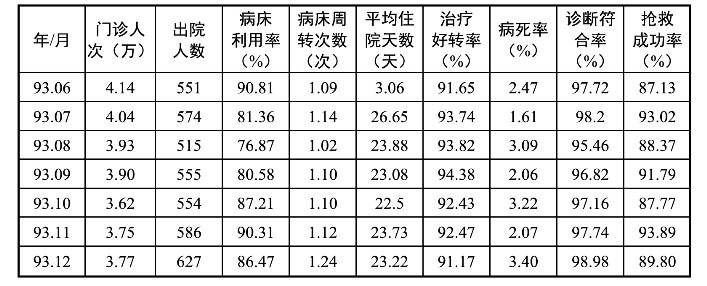
表4-2　某大型医院三年住院治疗情况

pagenumber_ebook=138,pagenumber_book=127

（续表）

pagenumber_ebook=139,pagenumber_book=128

医学图像数据聚类分析。随着脑部疾病（尤其是脑瘤）发生率的逐年上升，通过挖掘脑部医学图像来发现知识对辅助医生的诊断变得越来越重要。对于医生来说，确定脑部图像中是否存在占位是非常关键的。通过直接在每个图像的最基本元素——像素上进行两次聚类来判断可能存在的占位，然后使用分治的方法并行地对包含医学图像的对象进行分类，可实现基于像素聚类的脑部医学图像分类。

中医药数据聚类分析。证型是中医理论中认识疾病、诊断疾病、治疗疾病、判断疾病预后、进行病后调养的基础。每一个疾病都有几个不同的证型，每个证型对应了疾病不同阶段的不同病理实质。另外，证型也反映了疾病的轻重，反映了疾病的危险程度。胸痹心痛存在血瘀证一直是研究的热点，中医通过聚类分析证实，血瘀证是胸痹心痛最危险的临床证型，分析的结果是血瘀证与冠脉狭窄属于距离最近的一类。

应用聚类分析存在的问题：

（1）参数选择问题。聚类都涉及参数选择问题，如聚类数与距离函数（或密度函数）都需要人为设定，不同的参数设置通常会得到不同的聚类结果，尤其是面对高维稀疏数据时，聚类结果受距离函数（或密度函数）的影响更为突出。中医在症状、证候和复方药物的描述中具有高维性和稀疏性特征。例如，对3000多例糖尿病数据统计得知，常用的症状或中药名称约500种，证候描述约1000种，而每个患者描述的症状、中药与证候诊断约20种。

（2）聚类的单分配性。在“辨证”时，一种症状可表现在不同的证候中，一个患者可以表现出不同的证候；在利用复方“论治”时，一种中药可以出现在不同的复方里。所以在分析这些中医问题时，都不适合单纯使用聚类方法。

（3）中医药术语的语义复杂性。随着几千年语言文化的演变，中医术语普遍存在一词多义（Polysemy）和多词一义（Synonymy）的现象。如“喘”与“气喘”，“纳呆”与“厌食”以及“食欲不振”，“不寐”与“失眠”等在症状中的不同描述，在中草药中如“瓜蒌”与“瓜壳”，“姜”与“生姜”等的描述，在证候中如“伤寒”一词，可以是外感病的统称，也可以指外感风寒的感冒。在聚类挖掘中距离（或密度）的计算难以顾及特证词的语义问题。

2.聚类分析概述

聚类分析（Cluster Analysis）是一个将数据集中的所有数据，按照相似性划分为多个类别（Cluster，簇）的过程，簇是相似数据的集合。聚类分析将数据划分成有意义或有用的组（簇），其目标是组内的对象相互之间是相似的，而不同组中的对象是不同的。

聚类分析是一种无监督（Unsupervised Learning）分类方法：数据集中的数据没有预定义的类别标号（无训练集和训练的过程）。聚类分析之后，应尽可能保证类别相同的数据之间具有较高的相似性，而类别不同的数据之间具有较低的相似性。聚类分析仅根据在数据中发现的描述对象及其关系的信息将数据对象分组，聚类数据分类如图4-1所示。

pagenumber_ebook=140,pagenumber_book=129

图4-1　聚类数据示例

聚类分析在数据挖掘中的作用：（1）作为一个独立的工具来获得数据集中数据的分布情况。首先，对数据集执行聚类，获得所有簇；然后，根据每个簇中样本的数目获得数据集中每类数据的大体分布情况。（2）作为其他数据挖掘算法的预处理步骤。首先，对数据进行聚类——粗分类；然后，分别对每个簇进行特征提取和细分类，可以有效提高分类精度。(www.chuimin.cn)

有指导的学习和无指导的学习。有指导的学习（用于分类），模型的学习在被告知每个训练样本属于哪一类的“指导”下进行，新数据使用训练数据集中得到的规则进行分类。无指导的学习（用于聚类），每个训练样本的类编号是未知的，要学习的类集合或数量也可能是事先未知的，通过一系列的度量、观察来建立数据中的类编号或进行聚类。

聚类分析是把一个没有类别标记的样本集按某种标准分成若干个子集（类），使相似的样本尽可能归为一类，而不相似的样本尽量划分到不同的类中。思想：研究样本或指标（变量）之间存在着程度不同的相似性（亲疏），并按相似程度不同将指标和样本形成一个分类系统。

3.聚类分析的类型

在聚类分析中，通常我们将根据分类对象的不同分为Q型聚类分析和R型聚类分析两大类。

Q型聚类分析是对样本进行分类处理。当聚类把所有的观测记录（Cases）进行分类时，它把性质相似的观测分在同一个类，性质差异较大的观测分在不同的类。Q型聚类分析的优点是可以综合利用多个变量的信息对样本进行分类；分类结果是直观的，聚类谱系图非常清楚地表现其数值分类结果；聚类分析所得到的结果比传统分类方法更细致、全面、合理。

R型聚类分析是对变量进行分类处理。当聚类把变量（Variables）作为分类对象时，这种聚类用在变量数目比较多且相关性比较强的情形，目的是将性质相近的变量聚类为同一个类，并从中找出代表变量，从而减少变量个数以达到降维的效果。R型聚类分析的主要作用是，不但可以了解个别变量之间关系的亲疏程度，而且可以了解各个变量组合之间的亲疏程度。根据变量的分类结果以及它们之间的关系，可以选择主要变量进行回归分析或Q型聚类分析。

4.相似性度量

（1）描述两个样本之间的相似程度，距离

令Xi=（xi1，xi2，…，xik）是第i个样本观察值，Xj=（xj1，xj2，…，xjk）是第j个样本观察值，那么，样本Xi和Xj之间的欧氏距离：

pagenumber_ebook=141,pagenumber_book=130

距离越小，说明两个样本的性质越相似。它的取值大小受量纲影响，不稳定。因此，一般使用标准化的距离公式。

（2）描述两个指标变量之间的相似程度、相似系数

令Xs=（x1s，x2s，…，xns）是第s个指标变量，Xt=（x1t，x2t，…，xnt）是第t个指标变量，那么，指标变量Xs和Xt之间的相关系数：

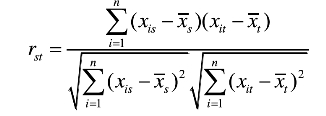
pagenumber_ebook=141,pagenumber_book=130

相关系数越大，说明两个指标变量的性质越相似，这是一个无量纲统计量。

用来进行类型划分的统计量，对样本进行划分的统计量为距离，常用的距离有欧式距离、马氏距离、兰氏距离；对变量进行划分的统计量为相似系数，常用的相似系数有夹角余弦、相关系数。

5.聚类分析原理与方法

聚类分析原理。聚类分析是按照一批样本的亲疏（即距离远近）程度进行分类分析。聚类的途径是确定样本（或变量）间的距离或相似系数。

基于划分方法的聚类（Partitioning Method）。基于“上限—中心点—重心”的原理，以距离作为数据集中不同数据间的相似性度量，将数据集划分成多个簇。给定一个有N个元组或者记录的数据集，分裂法将构造K个分组，每个分组就代表一个聚类，K＜N，而且这K个分组满足下列几个条件：每个分组至少包含一个数据记录；每一个数据记录属于且仅属于一个分组（在某些模糊聚类算法中可以放宽）。对于一个给定的K，算法首先给出一个初始的分组方法，以后通过反复迭代的方法改变分组，使得每一次改进之后的分组方案都较前一次好。好的标准就是同组记录越来越近，不同组记录越来越好。使用这个算法的基本思想：KMeans算法、Kmedoid算法、CLARANS算法。

医药数据聚类分析：大数据挖掘应用

相关推荐