贝叶斯决策理论是统计方法处理模式分类问题的基本理论之一。那么，利用贝叶斯公式可以得到后验概率基于最小错误率的贝叶斯决策规则为：如果，也就是说，如果p，那么将模式x赋予类ωi，即x∈ωi。上述理论中，每个类的出现概率以模式的条件概率密度函数必须是已知的。由于这些原因，贝叶斯决策理论在实际应用中通常要假设各种概率密度函数的解析式，以及从每类样本模式估计的必要参数。......
2025-09-29
贝叶斯分类算法演示及应用
【摘要】：，xn｝输出：未知样本X所属类别号3.朴素贝叶斯分类算法演示表3-9朴素贝叶斯示例数据集样本X7=｛打喷嚏，建筑工人，？朴素贝叶斯分类算法的优点在于容易实现，在大多数情况下所获得的结果比较好。
1.贝叶斯分类方法
贝叶斯分类方法是一种基于统计的学习方法，是一种利用概率统计知识进行学习分类的方法，如预测一个数据对象属于某个类别的概率。主要算法：朴素贝叶斯分类算法（Naive Bayes），贝叶斯信念网络分类算法等。
2.朴素贝叶斯分类算法（Naive Bayes）
朴素贝叶斯分类算法利用贝叶斯定理来预测一个未知类别的样本属于各个类别的可能性，选择其中可能性最大的一个类别作为该样本的最终类别。
设数据集为D，对应属性集：｛A1，A2，…，An，C｝
A1，A2，…，An是样本的属性变量，C是有m个取值C1，C2，…，Cm的类标号属性变量。
数据集D中的每个样本X可以表示为X=｛x1，x2，…，xn，Ci｝
朴素贝叶斯分类算法的概念描述如下：
P（Ci|X）＞P（Cj|X）
1≤j≤m，j≠i
根据贝叶斯定理：
类的先验概率P（Ci）可以用si/s来估计，其中si是数据集D中属于类Ci的样本个数，s是数据集D的样本总数。
朴素贝叶斯假定一个属性值对给定类的影响独立于其他属性值，属性之间不存在依赖关系，这样：
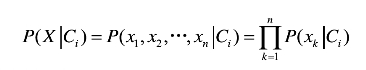
样本的各个属性变量之间：
独立事件，事件发生概率互相没影响。
P（A∩B）=P（A）P（B），P（A|B）=P（A）
相关事件，几个事件发生概率互相有影响。
P（A|B）！=P（A）
对未知样本X分类，对每个类Ci，计算P（X|Ci），样本X被指派到类别Ci中，当且仅当：P（X|Ci）P（Ci）＞P（X|Cj）P（Cj），1≤j≤m，j≠i
即X被指派到最大的类别中。
朴素贝叶斯分类算法的基本描述。
函数名：NaiveBayes
输入：类标号未知的样本X=｛x1，x2，…，xn｝
输出：未知样本X所属类别号
3.朴素贝叶斯分类算法演示
表3-9 朴素贝叶斯示例数据集
样本X7=｛打喷嚏，建筑工人，？｝
该问题描述如下：
样本X7=｛打喷嚏，建筑工人，？｝
类标号“疾病”有3个取值｛感冒，过敏，脑震荡｝
题目即求：
样本X7为“感冒”的概率P（疾病=感冒|X7）
样本X7为“过敏”的概率P（疾病=过敏|X7）
样本X7为“脑震荡”的概率P（疾病=脑震荡|X7）
样本X7将被预测为概率值大的那个类。
样本X7=｛打喷嚏，建筑工人，？｝
P（X7）=P（症状=打喷嚏，职业=建筑工人）
=P（症状=打喷嚏）P（职业=建筑工人）(https://www.chuimin.cn)
=3/6×2/6
=0.1667
根据朴素贝叶斯定理：
P（疾病=感冒|X7）
=P（X7|疾病=感冒）P（疾病=感冒）/P（X7）
=P（症状=打喷嚏|疾病=感冒）P（职业=建筑工人|疾病=感冒）P（疾病=感冒）/P（X7）
=2/3×1/3×3/6/P（X7）
=0.1111/P（X7）=0.6665
样本X7=｛打喷嚏，建筑工人，？｝
P（X7）=P（症状=打喷嚏，职业=建筑工人）
=P（症状=打喷嚏）P（职业=建筑工人）
=3/6×2/6
=0.1667
根据朴素贝叶斯定理：
P（疾病=过敏|X7）
=P（X7|疾病=过敏）P（疾病=过敏）/P（X7）
=P（症状=打喷嚏|疾病=过敏）P（职业=建筑工人|疾病=过敏）P（疾病=过敏）/P（X7）
=1/1×1/7×1/6/P（X7）
=0.0238/P（X7）=0.1428
根据朴素贝叶斯定理：
P（疾病=脑震荡|X7）
=P（X7|疾病=脑震荡）P（疾病=脑震荡）/P（X7）
=P（症状=打喷嚏|疾病=脑震荡）P（职业=建筑工人|疾病=脑震荡）P（疾病=脑震荡）/P（X7）
=1/7×1/2×2/6/P（X7）
=0.0238/P（X7）=0.1428
该问题描述如下：
样本X7=｛打喷嚏，建筑工人，？｝
计算：
P（疾病=感冒|X7）=0.6665
P（疾病=过敏|X7）=0.1428
P（疾病=脑震荡|X7）=0.1428
样本X7将被预测为概率值大的那个类，即为“感冒”。
4.贝叶斯算法处理流程
第一阶段——准备阶段：该阶段为朴素贝叶斯分类做必要的准备。主要是依据具体情况确定特征属性，并且对特征属性进行适当划分。然后就是对一部分待分类项进行人工划分，以确定训练样本。这一阶段的输入是所有的待分类项，输出是特征属性和训练样本。分类器的质量很大程度上依赖于特征属性及其划分以及训练样本的质量。
图3-10 贝叶斯算法处理流程
第二阶段——分类器训练阶段：主要工作是计算每个类别在训练样本中出现的频率以及每个特征属性划分对每个类别的条件概率估计。输入的是特征属性和训练样本，输出的是分类器。
第三阶段——应用阶段：这个阶段的任务是使用分类器对待分类项进行分类，其输入的是分类器和待分类项，输出的是待分类项与类别的映射关系。
朴素贝叶斯分类算法的优点在于容易实现，在大多数情况下所获得的结果比较好。缺点：算法成立的前提是假设各属性之间互相独立，当数据集满足这种独立性假设时，分类准确度较高。而在实际领域中，数据集可能并不完全满足独立性假设。
相关文章
- 详细阅读
-
基于贝叶斯网络的相关分析方法优化详细阅读
贝叶斯网络是基于概率分析和图论对不确定性知识进行表示的推理模型，它是一种模拟人类推理过程中因果关系的不确定性处理模型。贝叶斯分类器是用于分类的贝叶斯网络，它是各种分类器中分类错误概率最小或者在预先给定代价的情况下平均风险最小的分类器。通过对纽约市曼哈顿区2014年至2017年的交通事故数据构造朴素贝叶斯网络，对事故中伤亡人数进行分析。图4.1相关性分析结果......
2025-09-29
-
多分类器融合及性能评估分类算法详细阅读
多分类器融合就是融合多个分类器提供的信息，得到更加精确的分类结果。多数据投票法和BKS方法均是决策层的多分类器融合方法。利用训练集数据学习获得一个分类器，然后使用测试数据集对该分类器分类精度进行评估。......
2025-09-29
-
决策树分类算法在医药领域的应用详细阅读
决策树可以用来对未知样本进行分类。决策树分类算法使用场景，这个监督式学习算法通常被用于分类问题，它同时适用于分类变量和连续因变量。信息增益是决策树常用的分枝准则，在树的每个结点上选择具有最高信息增益的属性作为当前结点的划分属性。......
2025-09-30
-
关联规则分类算法优化技巧详细阅读
如果后件“C”只有类别值，自然可以想到使用此规则进行分类。典型的关联规则分类算法有CBA、CMAR和CPAR[99]。CBA是由Liu B等人提出的，是最早的也是最简单的关联规则分类算法[99]。在一些典型的分类数据集的测试中，CBA算法的实验精度高于C 4.5。但与CMAR不同的是，CPAR只选择每组中的“最好的”K个规则进行分类计算。可见，关联规则分类算法是一类基于规则的算法，其基础是频繁项目的与运算。......
2025-09-29
-
用途和分类：全面解析应用及分类详细阅读
根据用途不同，断路器可配备不同的脱扣器或继电器。表5-10断路器配备的脱扣器和继电器的情况断路器的分类方式很多，如按使用类别分，有选择型和非选择型；按灭弧介质分，有空气式和真空式；按结构类型分，有万能式和塑壳式；按操作方式分，有有关人力操作和无关人力操作、有关动力操作和无关动力操作，以及储能操作之分；按极数可分为单极式、二极式、三极式和四极式；按安装方式又可分为固定式、插入式和抽屉式等。......
2025-09-29
-
C4.5分类算法在医药领域的应用详细阅读
在C4.5算法中采用概率的方法，为缺失值的每个可能值赋予一个概率，而不是简单地用最常见的值替代该缺失值。C4.5决策树的生长阶段算法伪代码：C4.5决策树的剪枝处理阶段算法伪代码：5.C4.5算法的优缺点与其他分类算法相比，C4.5分类算法具有如下优点：产生的分类规则易于理解，准确率较高。为适应大规模数据集，在C4.5后出现有SLIQ和SPRINT等算法。......
2025-09-30
-
条件概率、乘法公式、全概率公式、贝叶斯公式解详细阅读
，Bn两两互不相容，且满足B1∪B2∪…∪Bn=Ω），则当P>0（i=1，2，…，n）时，对任意事件A有注 使用全概率公式解题时，可按以下原则寻找完全事件组B1，B2，…，Bn都较A先发生.贝叶斯公式：设B1，B2，…精解 先引入有关事件：A1={甲表演}，A2={乙表演}，A3={丙表演}，B={一次命中一次未命中}，则由于B与A1，A2，A3有关，且A1，A2，A3是发生于B之前的一个完全事件组，因此由全概率公式得所以......
2025-09-30
相关推荐