健康医疗大数据典型应用。可以构建大数据平台来收集不同病例和治疗方案以及病人的基本特征，建立针对疾病特点的数据库，帮助医生进行疾病诊断。医疗行业的大数据应用一直在进行，但是数据并没有完全打通，基本都是孤岛数据，没办法进行大规模的应用。健康医疗大数据在医疗行业治理方面的典型应用：卫生体制改革评估监测。大数据在疾病预测中的作用。大数据在临床业务、付款和定价、研发、大数据基因等方面的应用。......
2023-11-08
大数据挖掘技术在医药领域中的贝叶斯公式应用
【摘要】：，n），则3.贝叶斯定理贝叶斯，在《An Essay towards solving a Problem in the Doctrine of Chances》中给出了贝叶斯定理。其基本求解公式：贝叶斯公式：P（B|A）是根据A判断其属于类别B的概率，称为后验概率。
1.条件概率
若（Ω，F，P）是一个概率空间，B∈F，且P（B）＞0，对任意的A∈F，则
为在事件B发生的条件下，事件A发生的条件概率。
乘法定理：
设P（A）＞0，则有
P（AB）=P（B|A）P（A）=P（A|B）P（B）
图3-6 集合之间的关系A
图3-7 集合之间的关系B
对立事件：A'。（要么发生A，要么发生A'）A、A'互为穷举事件。
互斥事件：两个事件只有一个会发生（互斥与穷举不一样）。
相交事件：两个事件有可能同时会发生。
P（A∪B）=P（A）+P（B）-P（A∩B）
相关事件：几个事件发生概率互相有影响。
P（A|B）！=P（A）
独立事件：事件发生概率互相没影响。
P（A∩B）=P（A）P（B），P（A|B）=P（A）
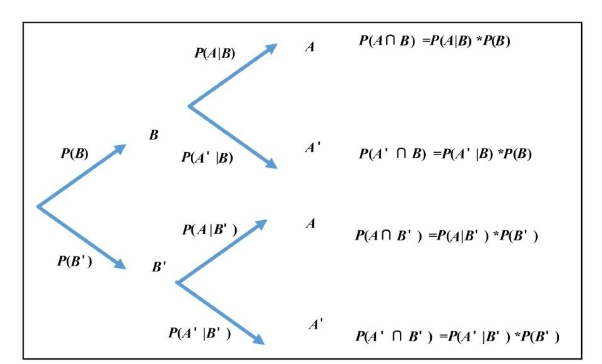
图3-8 决策树示例
2.样本空间的划分
定义设Ω为试验E的样本空间，A为E的事件，B1，B2，…，Bn为Ω的一个划分，且P（Bi）＞0（i=1，2，…，n），则
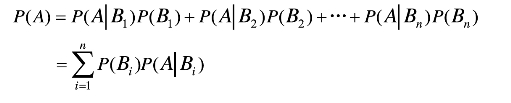
其中，BjBj=∅，i，j=1，2，…，n；且B1∪B2∪…∪Bn=Ω
图3-9 样本空间的划分
A=AΩ=A∩（B1∪B2∪…∪Bn）
=AB1∪AB2∪…∪ABn
说明：全概率公式的主要用途在于它可以将一个复杂事件的概率计算问题分解为若干个简单事件的概率计算问题，最后应用概率的可加性求出最终结果。(www.chuimin.cn)
设Ω为试验E的样本空间，A为E的事件，B1，B2，…，Bn为Ω的一个划分，且P（A）＞0，P（Bi）＞0（i=1，2，…，n），则
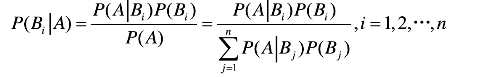
3.贝叶斯定理
贝叶斯（Thomas Bayes，1701—1761），在《An Essay towards solving a Problem in the Doctrine of Chances》中给出了贝叶斯定理。
它解决了两个事件条件概率的转换问题：
4.条件概率与贝叶斯公式
条件概率：P（A|B）表示事件B已经发生的前提下，事件A发生的概率，叫作事件B发生下事件A的条件概率。其基本求解公式：
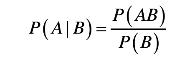
贝叶斯公式：P（B|A）是根据A判断其属于类别B的概率，称为后验概率。P（B）是直接判断某个样本属于B的概率，称为先验概率。P（A|B）是在类别B中观测到A的概率，P（A）是在数据库中观测到A的概率。
5.条件概率与贝叶斯公式的应用
一个医疗诊断问题有两个可选的假设：病人有癌症、病人无癌症。可用数据来自化验结果：正+和负-；有先验知识：在所有人口中，患病率是0.008；对确实有病的患者的化验准确率为98%，对确实无病的患者的化验准确率为97%；总结如下：
P（cancer）=0.008，P（-cancer）=0.992
P（+|cancer）=0.98，P（-|cancer）=0.02
P（+|-cancer）=0.03，P（-|-cancer）=0.97
问题1：假定有一个新病人，化验结果为正，是否应将病人断定为有癌症？
求后验概率P（cancer|+）和P（cancer|-）
总结如下：
P（cancer）=0.008，P（cancer）=0.992
P（+|cancer）=0.98，P（-|cancer）=0.02
P（+|cancer）=0.03，P（-|cancer）=0.97
问题2：假定有一个新病人，化验结果为正，是否应将病人断定为有癌症？
求后验概率P（cancer|+）和P（cancer|+）
P（cancer|+）=［P（+|cancer）P（cancer）］/P（+）=0.98×0.008/P（+）
P（+）=P（+|cancer）P（cancer）+P（+|cancer）P（cancer）
=0.98×0.008+0.03×0.992
P（cancer|+）=0.0078/（0.0078+0.0298）=0.21
有关大数据挖掘技术及其在医药领域的应用的文章
- 详细阅读
-
大数据挖掘技术在医药领域中的数据库与数据仓库详细阅读
数据库由数据库管理系统统一管理，数据的插入、修改和检索均要通过数据库管理系统进行。软件主要包括操作系统、各种宿主语言、实用程序以及数据库管理系统。数据库管理系统是一种系统软件，它的主要功能是维护数据库并有效地访问数据库中任意部分数据。对数据库的维护包括保持数据的完整性、一致性和安全性。数据仓库的多维特征满足以多维数据为核心的多维数据分析。......
2023-11-08
-
大数据挖掘技术在医药领域的应用详细阅读
打开VMware Workstation→点击文件→新建虚拟机。图9-2选择典型（推荐）选择“安装程序光盘映像文件”，选择指定的CentOS系统的.iso文件，点击“下一步〉”。图9-10在CentOS 6中安装VMware Tools重启CentOs 6。图9-11CentOS 6重启输入密码zkpk，登录进系统。图9-12CentOS 6安装完成下面克隆HadoopSlave。图9-14设置克隆虚拟机选项创建完整克隆。图9-16命名虚拟机图9-17正在准备克隆虚拟机图9-18正在克隆虚拟机点击“关闭”按钮后，发现“HadoopSlave”虚拟机已经在左侧的列表栏中。......
2023-11-08
-
大数据挖掘技术在医药领域中的特征提取成果详细阅读
以打鼾声声音特征提取为例，在基于机器学习的生物医学数据分析中，特征提取在大量医学数据中显得十分繁重而耗时。于月娜对宫颈细胞进行了图像分割和特征提取的研究。在对宫颈细胞特征提取方面的研究中，选取了合适的形状与纹理特征，通过KMeans算法进行深入研究。任丽晔对表面肌电信息进行特征提取，对不同的特征向量进行对比，选择最佳的特征向量，基于小波变换的特征提取反映信号局部性信息和时段信号变化的剧烈程度。......
2023-11-08
-
HBaseShell:在医药领域的大数据挖掘详细阅读
在HBase Shell提示符下执行help命令可列出所有命令列表。命名空间类命令命名空间是对表的逻辑分组，HBase可以针对命名空间分配资源限额，指定HRegionServer子集，进行安全管理等。大多数配置更改后必须重新启动HBase集群才能生效，与HRegion压缩、拆分相关的参数可以动态更改，更改后在HBase Shell中执行update_all_config命令即可生效。......
2023-11-08
-
大数据挖掘技术在医药领域的应用实例详细阅读
MapReduce编程：编写WordCount类，实现Mapper接口，实现Reducer接口，配置作业，代码测试，打包发布。其中，key为该行在文本中的偏移量，value值为这一行的内容。Map处理将分割好的〈key，value〉对作为map（）方法的输入，然后由用户定义的map（）方法进行Map处理，生成新的〈key，value〉对。Reduce处理首先，Reduce端接收到来自Map端的数据后，对数据进行排序，如图5-27Reduce端排序结果所示。......
2023-11-08
-
大数据挖掘在医药领域的应用详细阅读
数据挖掘就是从大量的、不完全的、有噪声的、模糊的、随机的数据中，提取隐含在其中的、人们事先不知道的、但又是潜在有用的信息和知识的过程。数据挖掘的替换词，包括数据库中的知识挖掘、知识提炼、数据/模式分析、数据考古、数据捕捞、信息收获，等等。数据挖掘方面更多的国际会议，如PAKDD，PKDD，SIAM-Data Mining，ICDM，DaWaK，SPIE-DM等。......
2023-11-08
-
大数据挖掘技术在医药领域的应用及数据采集详细阅读
表7-1数据采集按照数据来源划分，大数据的三大主要来源为商业数据、互联网数据与物联网数据。物联网数据的特点主要包括：物联网中的数据量更大，物联网中的数据传输速率更高，物联网中的数据更加多样化，物联网对数据真实性的要求更高。随着物联网技术、智能设备的发展，这种基于传感器的数据采集会越来越多，相应对于其的研究和应用也会越来越重要。......
2023-11-08
相关推荐