决策树可以用来对未知样本进行分类。决策树分类算法使用场景,这个监督式学习算法通常被用于分类问题,它同时适用于分类变量和连续因变量。信息增益是决策树常用的分枝准则,在树的每个结点上选择具有最高信息增益的属性作为当前结点的划分属性。......
2023-11-08
1.CART算法概述
CART(Classification and Regression Tree)算法,由美国斯坦福大学和加州大学伯克利分校的Breiman等人于1984年提出。CART决策树采用的是二元递归划分方法,能够处理连续属性数据和标称属性作为预测变量和目标变量下的分类。当输出变量是标称属性数据时,所建立的决策树称为分类树(Classification Tree),用于分类的预测。当输出变量为数值型变量时,所建立的决策树称为回归树(Regression Tree),用于数值的预测。随机森林是通过将很多的决策树组合而成的,随机森林采用CART算法。
Gini系数是Breiman于1984年提出来的,主要用在CART算法中。与C4.5相比,CART算法的主要差别体现在:
(1)CART为二叉树,而C4.5可以为多叉树。
(2)CART中的输入变量和输出变量可以是分类型也可以是数值型,而C4.5的输出变量只能是分类型。
(3)CART使用Gini系数作为变量的不纯度量,而C4.5使用信息增益率。
(4)如果目标变量是标称的,并且具有两个以上的类别,则CART可能考虑将目标类别合并成两个超类别。
(5)如果目标变量是连续的,则CART算法找出一组基于树的回归方程来预测目标变量。
(6)对于缺失值的处理方法不同,CART采用代理测试(Surrogate)来估计测试的输出值,而C4.5直接将其分配到该分支中概率最大的分类。
(7)对决策树的剪枝方法不同。
分类回归树的建树过程是对训练集反复划分的过程,涉及如何从多个属性中选择当前最佳划分属性的问题。另外,针对CART的分类树和回归树,它们的计算方法有所不同,数值型和分类型属性变量的计算方法也存在差异。
2.属性的选择标准
ID3使用信息增益作为属性选择标准,C4.5使用信息增益率作为属性选择标准。CART算法使用Gini系数来度量对某个属性变量测试输出的两组取值的差异性。理想的分组应该尽量使两组中样本输出变量取值的差异性总和达到最小,即“纯度”最大,也就是使两组输出变量取值的差异性下降最快,“纯度”增加最快。
设t为分类回归树中的某个节点,称函数为Gini系数:
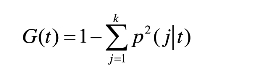
k为当前属性下测试输出的类别数,p(j|t)为节点t中样本测试输出取类别j的概率。
设t为一个节点,ξ为该节点的一个属性分枝条件,该分枝条件将节点t中样本分别分到左分支SL和右分支SR中,称为在分枝条件ξ下节点t的差异性损失:
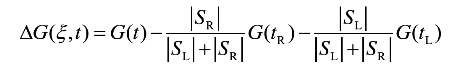
其中,G(t)为划分前测试输出的Gini系数,|SR|和|SL|分别表示划分后左右分枝的样本个数。为使节点t尽可能地纯,我们需选择某个属性分枝条件ξ使该节点的差异性损失尽可能大。用ξ(t)表示所考虑的分枝条件ξ的全体,则选择的分枝条件应为,
![]()
3.分类树与回归树的属性选择
分类树的属性选择:对于CART分类树的属性选择,针对属性类型分为分类型和数值型,方法有所不同。对于分类型属性,由于CART只能建立二叉树,对于取多个值的属性变量,需要将多类别合并成两个类别,形成“超类”,然后计算“超类”下样本测试输出取值的差异性。对于数值型属性,方法是将数据按升序排序,然后从小到大依次以相邻数值的中间值作为分隔,将样本分为两组,并计算所得组中样本测试输出取值的差异性。理想的分组是使两组中样本测试输出取值的差异性总和达到最小,即“纯度”最大,也就是使两组输出变量取值的差异性下降最快,“纯度”增加最快。
回归树的属性选择:回归树确定当前最佳分组变量的策略与分类树相同,主要不同在于度量节点测试输出值差异性的指标有所不同,采用方差作为指标。其定义为,
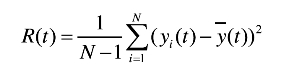
其中,t为节点,N为节点t所含的样本个数,y(it)为节点t中测试输出变量值,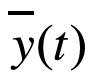 为节点t中测试输出变量的平均值。于是,差异性损失的度量指标为方差的减少量,其定义为(www.chuimin.cn)
为节点t中测试输出变量的平均值。于是,差异性损失的度量指标为方差的减少量,其定义为(www.chuimin.cn)
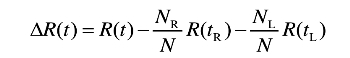
其中,R(t)和N分别为分组前输出变量的方差和样本个数,R(tR)、NR和R(tL)、NL分别为分组后右子树的方差和样本量以及左子树的方差和样本量,使达到最大的属性变量为当前最佳划分属性变量。
4.CART算法描述

5.基尼指标
在CART算法中,基尼不纯度表示一个随机选中的样本在子集中被分错的可能性。
基尼不纯度为这个样本被选中的概率乘以它被分错的概率。
假设y的可能取值为{1,2,…,m},令fi是样本被赋予i的概率,则基尼指数可以通过如下计算:
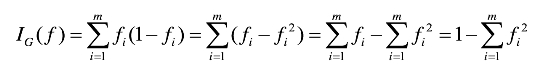
Gini指标,用来度量数据集的不纯度:
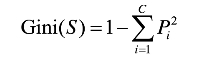
其中,P是S中类别i的概率。
Gini越小,数据越纯。
CART中计算Gini指标考虑每个属性上的二元划分,根据训练数据集S中的属性F将S分成的S1和S2,则给定划分的Gini指标如下公式所示:
最小化Gini指标:
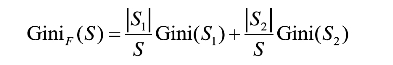
6.选择最佳分割点
数值型变量,对记录的值从小到大排序,计算每个值作为临界点产生的子节点的异质性统计量,能够使异质性减小程度最大的临界值便是最佳的划分点。
分类型变量,列出划分为两个子集的所有可能组合,计算每种组合下生成子节点的异质性。同样,找到使异质性减小程度最大的组合作为最佳划分点。
最好的划分就是使得Gini最小的划分。
7.C4.5算法和CART算法比较
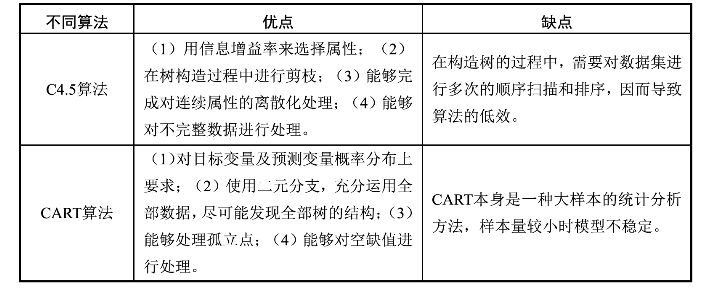
C4.5算法和CART算法比较如表3-8所示。
表3-8 C4.5算法和CART算法比较
有关大数据挖掘技术及其在医药领域的应用的文章

决策树可以用来对未知样本进行分类。决策树分类算法使用场景,这个监督式学习算法通常被用于分类问题,它同时适用于分类变量和连续因变量。信息增益是决策树常用的分枝准则,在树的每个结点上选择具有最高信息增益的属性作为当前结点的划分属性。......
2023-11-08

KMeans可能由于初始值选择的不同,导致最终的结果不同。图4-4KMeans算法迭代过程假设对于相同的样本数据,若随机选择的两个初始点为序号4和7。对于同一个数据集,由于KMeans算法对初始选取的聚类中心敏感,因此可用该准则评价聚类结果的优劣。通常,对于任意一个数据集,KMeans算法无法达到全局最优,只能达到局部最优。......
2023-11-08

在C4.5算法中采用概率的方法,为缺失值的每个可能值赋予一个概率,而不是简单地用最常见的值替代该缺失值。C4.5决策树的生长阶段算法伪代码:C4.5决策树的剪枝处理阶段算法伪代码:5.C4.5算法的优缺点与其他分类算法相比,C4.5分类算法具有如下优点:产生的分类规则易于理解,准确率较高。为适应大规模数据集,在C4.5后出现有SLIQ和SPRINT等算法。......
2023-11-08

从频繁项目集中生成所有可信关联规则,置信度大于minconf的规则为可信关联规则。C3:{柴胡,黄芩,清半夏}:2F3:{柴胡,黄芩,清半夏}:23.Apriori算法流程4.候选项集生成算法候选项集生成算法根据长度为k-1的频繁项目集Fk-1,经过两个步骤生成长度为k的候选项集Ck。......
2023-11-08

分类是一种基本的数据分析方式,根据其特点,可将数据对象划分为不同的部分和类型,再进一步分析,能够进一步挖掘事物的本质。分类分析的用途:解释和预报。......
2023-11-08

聚类分析的算法可以分为划分的方法、层次的方法、基于密度的方法、基于网格的方法、基于模型的方法等,其中,前两种方法最常用。图4-6层次聚类法示例4.基于网格的方法基于网格的聚类方法采用一个网格数据结构,把对象空间量化为有限数目的单元,形成了一个网格结构。......
2023-11-08

关于分类和回归模型的各种评估方法,一种是处理分类任务的模型,一种是预测回归的模型,这两种模型的评估方法也不完全一致,下面就来分别介绍两种类型模型的各种评估手段。AUC可以说是用单个数字总结模型性能的最好方法,其实就是ROC曲线下方的面积大小。平均绝对误差可以避免误差相互抵消的问题,因而可以准确反映实际预测误差的大小。MAE可以表示预测与实际结果的接近程度。以上即为两种模型的常用评估方法。......
2023-11-08
相关推荐