1.ID3分类算法
ID3分类算法由Quinlan于1986年提出，它使用信息增益（Information Gain）作为属性的选择标准。首先检测所有的属性，选择信息增益最大的属性产生决策树结点，由该属性的不同取值建立分支；再对各分支的子集递归调用该方法建立决策树结点的分支，直到所有子集仅包含同一个类别的数据为止；最后得到一棵决策树，它可以用来对新的样本进行分类。
2.信息熵
信息熵（Entropy，也称熵）用来度量一个属性的信息量。假定S为训练集，S的目标属性C具有m个可能的类标号值，C=｛C1，C2，…，Cm｝，假定训练集S中，Ci在所有样本中出现的频率为pi（i=1，2，3，…，m），则该训练集S所包含的信息熵定义为，
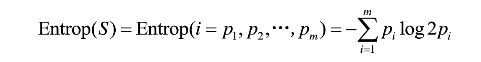
熵越小表示样本对目标属性的分布越纯，反之，熵越大表示样本对目标属性分布越混乱。
表3-5 Weather数据集
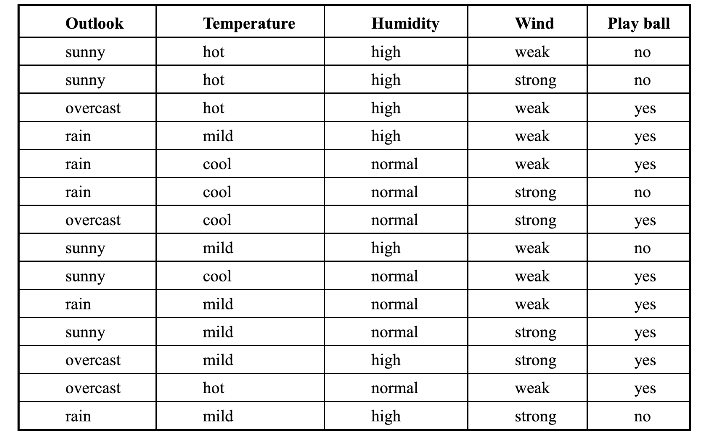
考虑Weather数据集如下，求weather数据集关于目标属性play ball的熵。
解答：令Weather数据集为S，其中有14个样本，目标属性play ball有两个值｛C1=yes，C2=no｝。14个样本的分布：9个样本的类标号取值为yes，5个样本的类标号取值为No。C1=yes在所有样本S中出现的概率为9/14，C2=no在所有样本S中出现的概率为5/14。
因此数据集S的熵为：
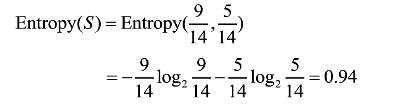
3.信息增益
信息增益是划分前样本数据集的不纯程度（熵）和划分后样本数据集的不纯程度（熵）的差值。假设划分前样本数据集为S，并用属性A来划分样本集S，则按属性A划分S的信息增益Gain（S，A）为样本集S的熵减去按属性A划分S后的样本子集的熵：
Gain（S，A）=Entropy（S）-EntropyA（S）
按属性A划分S后的样本子集的熵定义如下：假定属性A有k个不同的取值，从而将S划分为k个样本子集｛S1，S2，...，Sk｝，则按属性A划分S后的样本子集的信息熵为：
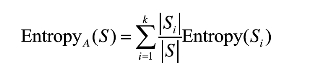
其中|Si|（i，=1，2，…，k）为样本子集Si中包含的样本数，|S|为样本集S中包含的样本数。
信息增益越大，说明使用属性A划分后的样本子集越纯，越有利于分类。
以Weather数据集为例，设该数据集为S，假定用属性wind来划分S，求S对属性wind的信息增益。
解答：（1）首先由前例计算得到数据集S的熵值为0.94；（2）属性wind有两个可能的取值｛weak，strong｝，它将S划分为两个子集｛S1，S2｝，S1为wind属性取值为weak的样本子集，共有8个样本；S2为wind属性取值为strong的样本子集，共有6个样本。下面分别计算样本子集S1和S2的熵。
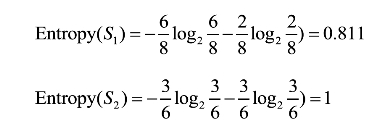
利用属性wind划分S后的熵：
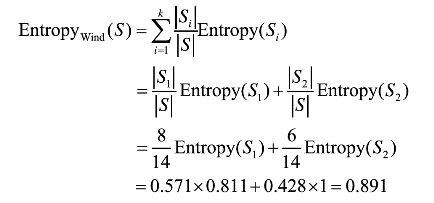
按属性wind划分数据集S所得的信息增益值：
Gain（S，wind）=Entropy（S）-Entropywind（S）
=0.94-0.891=0.049
4.ID3算法伪代码
函数：DT（S，F）；输入：训练集数据S，训练集数据属性集合F；输出：ID3决策树。
5.ID3建立决策树
第一步，数据集的构成。
数据集具有属性：outlook，temperature，humidity，wind.outlook=｛sunny，overcast，rain｝，temperature=｛hot，mild，cool｝，humidity=｛high，normal｝，wind=｛weak，strong｝。
第二步，ID3建立决策树。
首先，计算总数据集S对所有属性的信息增益，寻找根节点的最佳分裂属性：
Gain（S，outlook）=0.246
Gain（S，temperature）=0.029
Gain（S，humidity）=0.152
Gain（S，wind）=0.049
显然，这里outlook属性具有最高信息增益值，因此将它选为根结点。
接着，以outlook作为根结点，继续往下。思想是以outlook的可能取值建立分支，对每个分支递归建立子树。因为outlook有三个可能值，因此对根结点建立三个分支｛sunny，overcast，rain｝。那么，哪个属性用来划分根结点的Sunny分支最佳？overcast分支？Rain分支？
第三步，对outlook的sunny分支建立子树。
找出数据集中outlook=sunny的样本子集Soutlook=sunny，然后依次计算剩下三个属性对该样本子集Ssunny划分后的信息增益：
Gain（Ssunny，humidity）=0.971
Gain（Ssunny，temperature）=0.571
Gain（Ssunny，wind）=0.371
显然，humidity具有最高信息增益值，因此它被选为outlook结点下sunny分支下的决策结点。
第四步，采用同样的方法，依次对outlook的overcast分支、rain分支建立子树，最后得到一棵可以预测类标号未知的样本的决策树。
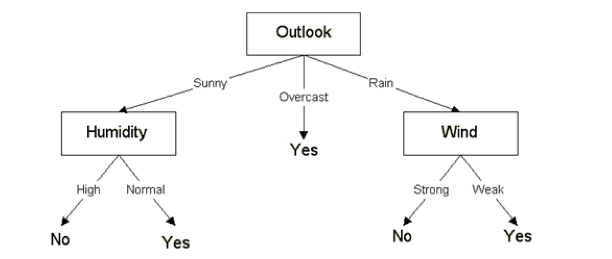
图3-1 Weather数据集的决策树示例
第五步，决策树对未知样本的预测。下面利用决策树对类标号未知的样本X进行预测：X=｛rain，hot，normal，weak，？｝。
6.ID3算法总结
ID3算法总结：ID3算法是所有可能的决策树空间中一种自上向下、贪婪的搜索方法。ID3搜索的假设空间是可能的决策树的集合；搜索目的是构造与训练数据一致的一棵决策树；搜索策略是爬山法，在构造决策树时从简单到复杂，用信息熵作为爬山法的评价函数。ID3算法的核心是在决策树各级结点上选择属性，用信息增益作为属性选择的标准，使得在每个非叶节点进行测试时都能获得关于被测数据最大的类别信息，使得该属性将数据集分成子集后，系统的熵值最小。
ID3算法优缺点分析。优点：理论清晰，方法简单，学习能力较强。缺点：（1）算法只能处理分类属性数据，无法处理连续型数据。（2）算法对测试属性的每个取值相应产生一个分支，且划分相应的数据样本集，这样的划分会导致产生许多小的子集。随着子集被划分得越来越小，划分过程将会由于子集规模过小所造成的统计特征不充分而停止。（3）ID3算法中使用信息增益作为决策树节点属性选择的标准，由于信息增益在类别值多的属性上计算结果大于类别值少的属性上的计算结果，这将导致决策树算法偏向选择具有较多分支的属性，因而可能导致过度拟合。在极端的情况下，如果某个属性对于训练集中的每个元组都有唯一的一个值，则认为该属性是最好的，这是因为对于每个划分都只有一个元组（因此也是一类）。
ID3算法评价。优点：理论清晰，算法简单，很有实用价值的示例学习算法；计算时间是例子个数、特征属性个数、节点个数之积的线性函数，总预测准确率较令人满意。缺点：（1）存在偏向问题，各特征属性的取值个数会影响信息量的大小；（2）特征属性间的相关性强调不够，是单变元算法；（3）对噪声较为敏感，训练数据的轻微错误会导致结果的不同；（4）结果随训练集记录个数的改变而不同，不便于进行渐进学习。
7.基于ID3算法的流感数据集分析
已知：流感训练数据集，预定义两个类别；
求：各类别的描述特征。(www.chuimin.cn)
表3-6 流感训练数据集
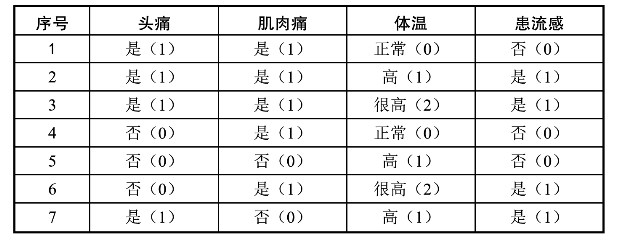
例题中各数据的属性及其取值分别为，
类别：是、否；——u1、u2
头痛A1：是、否；肌肉痛A2：是、否；体温A3：很高、高、正常
选择全部数据记录，求先验熵（对类别）：
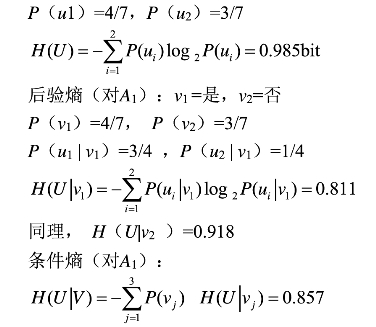
互信息（对A1）：
I（A1）=H（U）-H（U|V）=0.128
同理，有：
I（A2）=0.006，I（A3）=0.592
I（A3）值最大，所以选择“体温”作为决策树的根节点，将其三个取值分别作为三个分支，并划分原数据集合为三个子集。
判断子集中各记录是否属于同一类别，若是则在树上作标记，否则对子集重复上述步骤。
结果：流感数据集的决策树如图3-2所示。
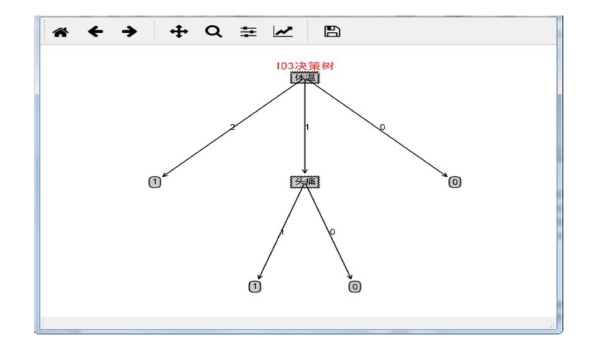
图3-2 流感数据集的决策树示例
程序运行过程如下：
8.基于ID3算法的隐形眼镜选择
在一个眼镜店，假如眼镜店的店员利用下面这棵决策树来决定卖给客户什么样的隐形眼镜镜片，那么他就可以用客户眼睛基本情况调查表来构造这棵决策树，用决策树来判断隐形眼镜镜片的类型。
戴了隐形眼镜镜片后泪流量减少，眼睛干涩，这类人不适宜使用隐形眼镜镜片。
戴了隐形眼镜镜片后泪流量正常，对于眼睛不散光的客户，建议他使用软性隐形眼镜镜片。
戴了隐形眼镜镜片后泪流量正常，对于眼睛散光的客户，建议他使用硬性隐形眼镜镜片。
表3-7 隐形眼镜选择数据集
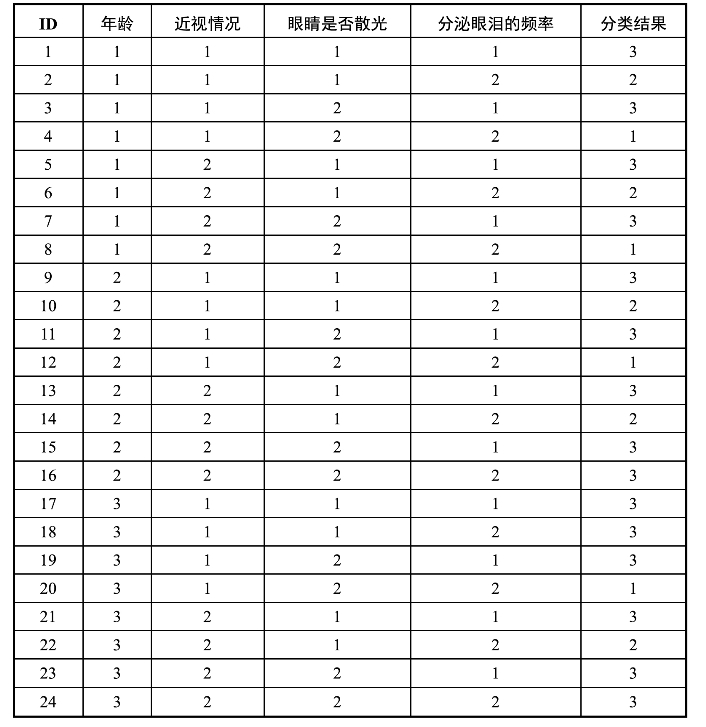
第一列的1～24，对应数据的ID。
第二列的1～3，对应病人的年龄（age of patient），分别是青年（young）、中年（pre-presbyopic）、老年（presbyopic）。
第三列的1和2，对应近视情况（spectacle prescription），分别是近视（myope）、远视（hypermetrope）。
第四列的1和2，对应眼睛是否散光（astigmatic），分别是不散光（no）、散光（yes）。
第五列的1和2，对应分泌眼泪的频率（tear production rate），分别是很少（reduce）、普通（normal）。
第六列的1～3，则是最终根据以上数据得到的分类，分别是硬性的隐形眼镜（hard）、软性的隐形眼镜（soft）、不需要戴眼镜（no lenses）。
经过计算，可以得到当前使用的数据集，熵为1.32608752536。
然后划分数据集，可以根据数据集、特征索引和特征值来划分数据集。
取最佳特征值，需要计算信息增益，即将单独一个特征值提取出来，计算该特征值每个分支划分出数据集的熵的求和，然后用总数据集的熵减去它。计算四个特征值的信息增益，得到以下数据：
0：0.0393965036461
1：0.0395108354236
2：0.377005230011
3：0.548794940695
通过计算可以得出特征值的优先级，tear production rate〉astigmatic〉spectacle prescription〉age of patient。
接下来，有了以上的计算函数，可以开始创建决策树。使用字典类型去存储，用键代表分支节点，值代表下一个节点或者叶子节点，代码如下：
测试代码，打印创建出的决策树：
输出：
可以看出，这是一个比较长的字典嵌套结构，但是这样看上去很不直观，为了让这个决策树能直观地显示出来，导入图形化模块matplotlib，用来把决策树画出来。
新写一个treePlotter脚本，脚本中添加计算决策树叶节点数量及深度的函数，用以计算画布的高宽布局。通过计算两个节点中点坐标的函数，确定分支属性的位置，最终画出决策树。以下是脚本代码：
在测试代码上调用创建决策树图像的函数：treePlotter.createPlotPlus（myTree），得到最终图像如图3-3所示。
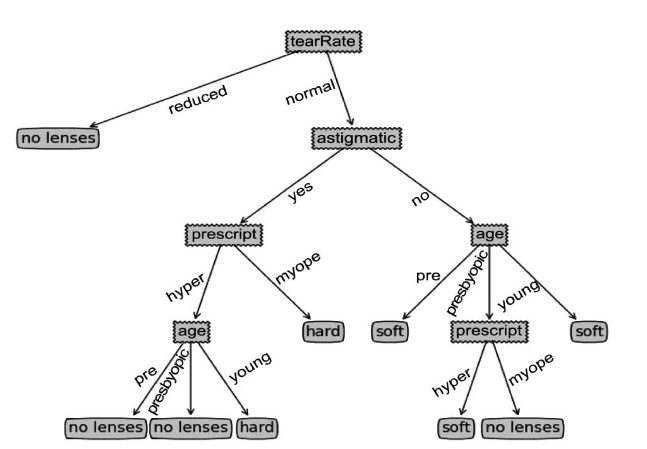
图3-3 眼镜选择的决策树示例
有关大数据挖掘技术及其在医药领域的应用的文章
打开VMware Workstation→点击文件→新建虚拟机。图9-2选择典型（推荐）选择“安装程序光盘映像文件”，选择指定的CentOS系统的.iso文件，点击“下一步〉”。图9-10在CentOS 6中安装VMware Tools重启CentOs 6。图9-11CentOS 6重启输入密码zkpk，登录进系统。图9-12CentOS 6安装完成下面克隆HadoopSlave。图9-14设置克隆虚拟机选项创建完整克隆。图9-16命名虚拟机图9-17正在准备克隆虚拟机图9-18正在克隆虚拟机点击“关闭”按钮后，发现“HadoopSlave”虚拟机已经在左侧的列表栏中。......
2023-11-08
分类是一种基本的数据分析方式，根据其特点，可将数据对象划分为不同的部分和类型，再进一步分析，能够进一步挖掘事物的本质。分类分析的用途：解释和预报。......
2023-11-08
在HBase Shell提示符下执行help命令可列出所有命令列表。命名空间类命令命名空间是对表的逻辑分组，HBase可以针对命名空间分配资源限额，指定HRegionServer子集，进行安全管理等。大多数配置更改后必须重新启动HBase集群才能生效，与HRegion压缩、拆分相关的参数可以动态更改，更改后在HBase Shell中执行update_all_config命令即可生效。......
2023-11-08
关于分类和回归模型的各种评估方法，一种是处理分类任务的模型，一种是预测回归的模型，这两种模型的评估方法也不完全一致，下面就来分别介绍两种类型模型的各种评估手段。AUC可以说是用单个数字总结模型性能的最好方法，其实就是ROC曲线下方的面积大小。平均绝对误差可以避免误差相互抵消的问题，因而可以准确反映实际预测误差的大小。MAE可以表示预测与实际结果的接近程度。以上即为两种模型的常用评估方法。......
2023-11-08
MapReduce编程：编写WordCount类，实现Mapper接口，实现Reducer接口，配置作业，代码测试，打包发布。其中，key为该行在文本中的偏移量，value值为这一行的内容。Map处理将分割好的〈key，value〉对作为map（）方法的输入，然后由用户定义的map（）方法进行Map处理，生成新的〈key，value〉对。Reduce处理首先，Reduce端接收到来自Map端的数据后，对数据进行排序，如图5-27Reduce端排序结果所示。......
2023-11-08
聚类分析的算法可以分为划分的方法、层次的方法、基于密度的方法、基于网格的方法、基于模型的方法等，其中，前两种方法最常用。图4-6层次聚类法示例4.基于网格的方法基于网格的聚类方法采用一个网格数据结构，把对象空间量化为有限数目的单元，形成了一个网格结构。......
2023-11-08
数据挖掘就是从大量的、不完全的、有噪声的、模糊的、随机的数据中，提取隐含在其中的、人们事先不知道的、但又是潜在有用的信息和知识的过程。数据挖掘的替换词，包括数据库中的知识挖掘、知识提炼、数据/模式分析、数据考古、数据捕捞、信息收获，等等。数据挖掘方面更多的国际会议，如PAKDD，PKDD，SIAM-Data Mining，ICDM，DaWaK，SPIE-DM等。......
2023-11-08
表7-1数据采集按照数据来源划分，大数据的三大主要来源为商业数据、互联网数据与物联网数据。物联网数据的特点主要包括：物联网中的数据量更大，物联网中的数据传输速率更高，物联网中的数据更加多样化，物联网对数据真实性的要求更高。随着物联网技术、智能设备的发展，这种基于传感器的数据采集会越来越多，相应对于其的研究和应用也会越来越重要。......
2023-11-08
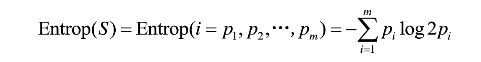
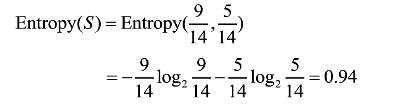
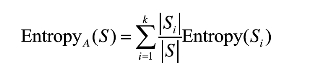
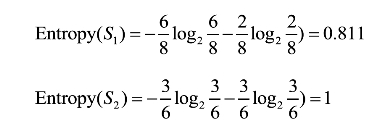
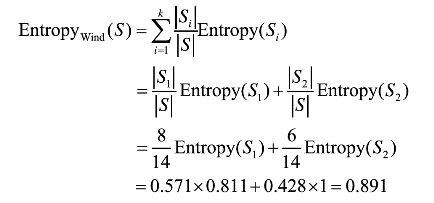
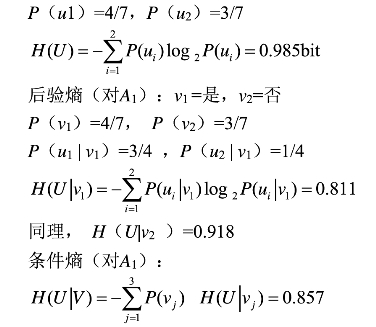
相关推荐