首页 理论教育单片机多语言编程：数制与运算

单片机多语言编程：数制与运算

2023-11-07 理论教育 版权反馈
【摘要】：将一个二进制数转换成十进制数表示，只需按权展开做一次10进制运算即可以完成。将一个十进制数转换成二进制数表示，是数据转换中较复杂的工作。做乘、除运算时，其法则与十进制数也是相同的。它不同于数值运算。二进制数可以进行按位的逻辑运算，每位之间相互独立，位与位之间不存在进位和借位的关系。

1.十进制、二进制和十六进制

十进制（Decimal）有进位计数的累积和进位特征。十进制数由0，1，2，…，9共10个数码表示，并遵循“逢十进一”的进位计数规则。十进制的计数基数是10。例如

780=7×102+8×101+0×100上式称为按“权”展开式。各位数的权值为10的幂，即个位数的权为100，十位数的权为101，百位数的权为102等。

二进制（Binary）遵循十进制数的分析过程，我们同样可以确定，二进制数要由两个数码表示，即0和1，并遵循“逢二进一”的进位计数规则。二进制数的计数基数是2，各位的权值为2的幂。例如，1101B=1×23+1×22+0×21+1×20=13。

十六进制（Hexadecimal）十六进制数要由16个数码表示，即0，1，2，…，9，A，B，C，D，E，F，并遵循“逢十六进一”的进位计数规则。十六进制的计数基数是16。在十六进制中A表示值为10的数码，B表示值为11的数码，…，F表示值为15的数码。各位的权值为16的幂。例如，3ABH=3×162+A×161+B×160=3×256+10×16+11×1=939。

2.各种进制的转换

二进制数与十进制数的相互转换，按如下步骤进行：

二进制数转换成十进制数。将一个二进制数转换成十进制数表示，只需按权展开做一次10进制运算即可以完成。

【例1-10】　将二进制数11101010B转换成十进制数

11101010B=1×27+1×26+1×25+0×24+1×23+0×22+1×21+0×20

=128+64+32+8+2=234

十进制数转换成二进制数。将一个十进制数转换成二进制数表示，是数据转换中较复杂的工作。这里我们只涉及整数部分，转换方法是将十进制整数除以2取余数，直到商为0。

【例1-11】　将十进制数45转换成二进制数

转换过程为

978-7-111-47138-7-Chapter01-56.jpg

转换结果为

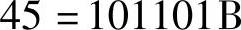
978-7-111-47138-7-Chapter01-57.jpg

由于我们的学习主要涉及8位二进制数的处理，若结果不够8位，要将已得的位数高两位补0，即45=00101101B，两种表示数值相同，为了阅读方便，统一用8位二进制数表示。

3.二进制数与十六进制数的相互转换

【例1-12】　将十六进制数3ACDH转换成二进制数

转换过程为

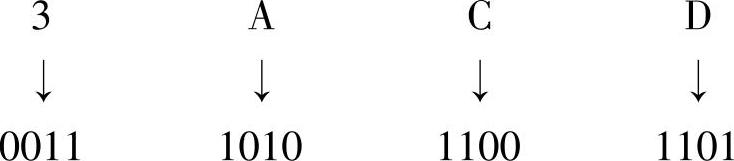
978-7-111-47138-7-Chapter01-58.jpg

转换结果为

3ACDH=0011101011001101B

二进制数转换为十六进制数。将二进制数转换为十六进制数，可以表述为以二进制数最低位为起点，向前每4位作为一组，若取到最高位时不足4位可补0代替，每一组4位二进制数即可写出对应的十六进制数，按由低到高位排列即得结果。

【例1-13】　将二进制数010101111011B转换为十六进制数

转换过程为

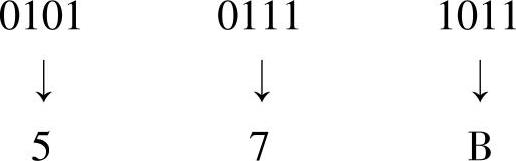
978-7-111-47138-7-Chapter01-59.jpg

转换结果为

010101111011B=57BH

4.二进制数的算术运算

对于二进制数的算术运算，像通常十进制数的算术运算一样，做加、减运算时，个位要对齐。做乘、除运算时，其法则与十进制数也是相同的。与十进制不同的是，在运算过程中始终要遵循“逢2进1”的运算规则。

（1）加法运算法则（见表1-2）

表1-2　加法运算法则

978-7-111-47138-7-Chapter01-60.jpg

【例1-14】　求00010011B+00100011B

运算过程为

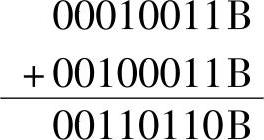
978-7-111-47138-7-Chapter01-61.jpg

故00010011B+00100011B=00110110B

验算00010011B=16+2+1=19

00100011B=32+2+1=35 19+35=54

结果00110110B=32+16+4+2=54，正确

【例1-15】　求11111111B+00000001B

运算过程为

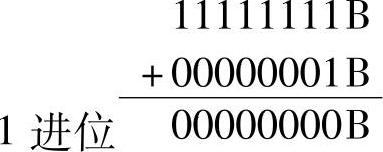
978-7-111-47138-7-Chapter01-62.jpg

由于只涉及8位二进制数，进位位无法显示

11111111B+00000001B=0进位位=1

验算11111111B=255

00000001B=1 255+1=256

结果100000000B=256进位位=1

（2）减法运算法则（见表1-3）

表1-3　减法运算法则

978-7-111-47138-7-Chapter01-63.jpg

【例1-16】　求00010110B-00001001B

运算过程为

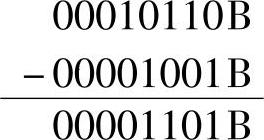
978-7-111-47138-7-Chapter01-64.jpg

故00010110B-00001001B=00001101B

验算00010110B=32 00001001B=9 32-9=13

结果00001101B=13 正确

【例1-17】　求00000000B-00000001B(www.chuimin.cn)

运算过程为

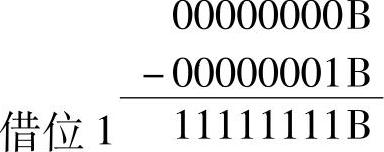
978-7-111-47138-7-Chapter01-65.jpg

故　00000000B-00000001B=11111111B

验算00000000B=0 00000001B=1 0-1=-1

结果11111111B=-1　因为若x=11111111B

x+1=0，x=-1

（3）乘法运算法则（见表1-4）

表1-4　乘法运算法则

978-7-111-47138-7-Chapter01-66.jpg

【例1-18】　求00001101B×00000110B

运算过程为

978-7-111-47138-7-Chapter01-67.jpg

故　00001101B*00000110B=01001110B

验算00001101B=13

00000110B=6 13*6=78

结果01001110B=78 正确

（4）除法运算法则（见表1-5）

表1-5　除法运算法则

978-7-111-47138-7-Chapter01-68.jpg

【例1-19】　求00001101B÷00000110B

运算过程为

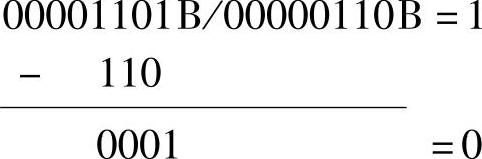
978-7-111-47138-7-Chapter01-69.jpg

故　00001101B/00000110B=10B=2

余数=0001B=1

验算00001101B=13

00000110B=6 13/6=2，余数=1

5.二进制数的逻辑运算

上面讲到，计算机中的数据是以二进制为基础的，只有“1”和“0”两个值，这是一种对应的逻辑值，而不能理解为数值。在生活中“真”和“假”，“对”和“错”都可以看作为逻辑值。如果“真”是1，“假”就是0，“高”是1，“低”就是0。对逻辑值，有一套特有的运算规则。它不同于数值运算。例如，对于逻辑值1+1=1。这在算术运算中是不成立的，但对逻辑值运算却是正确的。

二进制数可以进行按位的逻辑运算，每位之间相互独立，位与位之间不存在进位和借位的关系。

（1）逻辑与（AND）

逻辑与的运算法则与二进制乘法相类似。因此，与运算通常用“*”或“&”来表示，其运算法则见表1-6。

表1-6　逻辑与的运算法则

978-7-111-47138-7-Chapter01-70.jpg

由运算法则可知，逻辑与的意义是只有当参与运算的逻辑变量都为1时，与运算的结果才会为1。只要其中有一个为0，其结果就为0。

【例1-20】　逻辑与运算　10101111B&10011101B=10001101B

运算过程为

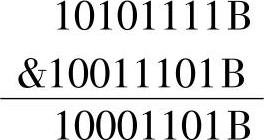
978-7-111-47138-7-Chapter01-71.jpg

（2）逻辑或（OR）

逻辑或的运算法则类似于二进制加法。因此，或运算通常用“+”或“|”表示，其运算法则见表1-7。

表1-7　逻辑或的运算法则

978-7-111-47138-7-Chapter01-72.jpg

由运算法则可知，逻辑或的意义是当参与运算的逻辑变量中有任意一个为1时，或运算的结果就为1。只有都为0时，其结果才为0。

【例1-21】　逻辑或运算　10101010B+01100110B=11101110

运算过程为

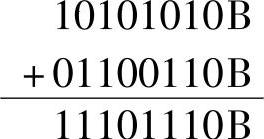
978-7-111-47138-7-Chapter01-73.jpg

（3）逻辑非（NOT）

逻辑非就是逻辑取反，用逻辑量再加一横线表示。例如，A的逻辑非即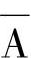978-7-111-47138-7-Chapter01-74.jpg。逻辑非的运算法则见表1-8。

表1-8　逻辑非运算的法则

978-7-111-47138-7-Chapter01-75.jpg

【例1-22】　若A=10101100B，则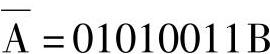978-7-111-47138-7-Chapter01-76.jpg。

（4）逻辑异或（XOR）

异或运算可以通过基本逻辑运算实现。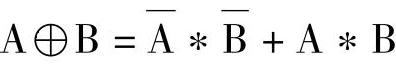978-7-111-47138-7-Chapter01-77.jpg，用“⊕”表示，逻辑异或运算法则见表1-9。

表1-9　逻辑异或运算法则

978-7-111-47138-7-Chapter01-78.jpg

【例1-23】　逻辑异或　10101100B⊕01100110B=11001010B

运算过程为

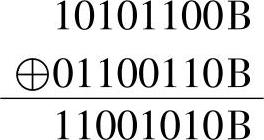
978-7-111-47138-7-Chapter01-79.jpg

由运算法则可知，逻辑异或运算是只有在两个逻辑变量的值不同时，其结果才为1。否则结果为0。用异或运算的结果可以很容易地判断两个逻辑变量是否相同。

逻辑运算在数据处理过程中经常使用。例如，A是一个8位二进制数，若要得到A的低4位数，只要做逻辑运算“A*00001111B”，高4位被屏蔽，结果就是低4位数。

有关零起点学习单片机多语言编程的文章

  • 三、增量运算在单片机多语言编程中的应用和验证 三、增量运算在单片机多语言编程中的应用和验证

    增量运算见表4-2。两种形式结果相同。但若增量运算符与其他运算符联合组成一个表达式，则增量运算符在变量前或变量后，其结果是不同的。证明程序运算结果正确。读者可自行在Keil μVision 2平台上验证。若下载到实验机，P0、P2、P3可以用逻辑笔观察结果。......

    2023-11-07

    详细阅读
  • 单片机多语言编程之if-else分支语句 单片机多语言编程之if-else分支语句

    if-else条件分支语句是选择结构的一种形式，是最常用的语句之一。这意味着如果if后面的表达式成立（不为0），则执行if下面的语句，否则直接向下执行。......

    2023-11-07

    详细阅读
  • 零起点学习单片机多语言编程-位运算的应用 零起点学习单片机多语言编程-位运算的应用

    位运算是以运算量的二进制位为单位所进行的运算。一般位逻辑运算都是以十六进制数形式进行。在右移运算中，左端的空位补0，右端移出位则舍弃。按条件将a=0x85，b=0x36，执行位运算具体如下：P3=a<<1，左移1位后a=00001010=0x0A显示正确，左位取消，右位补0。......

    2023-11-07

    详细阅读
  • 单片机多语言编程：I/O接口输出操作 单片机多语言编程：I/O接口输出操作

    程序点评：数据传送指令MOV将一组数据分别传送到P1口，做了输出口的操作。将8位立即数传送给累加器A，再由累加器A将数据传送到I/O接口的P1口，使P1.0灯亮。在I/O接口输出操作时不能将间接寄存器中的地址输出到P1口。......

    2023-11-07

    详细阅读
  • 零基础学习单片机多语言编程 零基础学习单片机多语言编程

    尽管单片机有许多特点，但仍然属于计算机的范围。这种特殊的语言就是程序设计语言，也就是由一系列语句组成的程序。程序设计语言从原理上可分为机器语言、汇编语言和高级语言三种类型，单片机也不例外。由于汇编语言指令具有直接对应机器语言指令的特点，因而生成的机器代码效率高，执行速度快，至今在单片机程序设计中仍被采用。在众多高级语言中，只有C语言成了应用于单片机系统的高级语言。......

    2023-11-07

    详细阅读
  • 零基础学单片机多语言编程 零基础学单片机多语言编程

    对单片机来说，可以用高级语言编程，也可用汇编语言编程，两种语言各有特点。像8051具有MCS51系列单片机的指令集。用助记符指令组成的计算机语言就称为汇编语言。......

    2023-11-07

    详细阅读
  • 中断概念与多语言编程 中断概念与多语言编程

    所谓中断，就是计算机为提高运行效率而采用的一种方式。当一个变量一旦发生要求的改变时，计算机立即自动触发中断，转向一段服务程序，执行完成后，自动返回主程序的原断点继续运行。④ES为串行口中断允许位。当几个通道同时发生中断时，计算机只能选择一个通道进行响应，即具有高优先级的通道才能被响应。⑥连续单击“跟踪”，由于a+1，a≠5，所以返回主函数继续等待下一次中断。......

    2023-11-07

    详细阅读
  • 学习单片机多语言编程，包括简易汇编语言 学习单片机多语言编程，包括简易汇编语言

    为此，出现了用代表指令意义的助记符表示指令。后面的字节称为“操作数”，表示端口的编号是00。将助记符表示的程序变换为包括地址和机器码在内的可执行程序的过程，称为“汇编”。对“宏”助记符指令进行的“汇编”，称为“简易汇编”。利用“宏”作为学习8051汇编语言和C语言的入门阶梯，对初学者是较好的一种选择。......

    2023-11-07

    详细阅读