虚拟内存可用于运行较为大型的应用程序,但不适于时间条件苛刻的应用程序。有些情况下,可能会出现更少的运行时内存使用。并且,如果VI前面板或程序框图的规模超过了屏幕可显示的范围,将其分为子VI更便于其使用。特定的程序框图可阻止LabVIEW重复使用数据缓冲区。在子VI中通过一个条件显示控件能阻止LabVIEW对数据缓冲区的使用进行优化。......
2023-11-07
概率与统计的理论方法在技术领域的应用十分广泛,在信号的测试与处理中,它既可控制整个过程,又可以提高信号的分辨率。
概率与统计VI用于执行概率、叙述性统计、方差分析和插值函数方面。其子选板函数如图9-34所示。
图9-34 “概率与统计”子选板
概率(Probability)一词来源于拉丁语“Probabilitas”, 又可以解释为 Probity。Probity的意思是“正直,诚实”,在欧洲probity用来表示法庭案例中证人证词的权威性,且通常与证人的声誉相关。总之与现代意义上的概率“可能性”含义不同。
1.古典定义
如果一个试验满足两条:
1)试验只有有限个基本结果;
2)试验的每个基本结果出现的可能性是一样的。
这样的试验便是古典试验。
对于古典试验中的事件A,它的概率定义为:P(A)=m/n,其中n表示该试验中所有可能出现的基本结果的总数目。m表示事件A包含的试验基本结果数。这种定义概率的方法称为概率的古典定义。
2.频率定义
随着人们遇到问题的复杂程度的增加,等可能性逐渐暴露出它的弱点,特别是对于同一事件,可以从不同的等可能性角度算出不同的概率,从而产生了种种悖论。另一方面,随着经验的积累,人们逐渐认识到,在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示出一定的稳定性。R.von米泽斯把这个固定数定义为该事件的概率,这就是概率的频率定义。从理论上讲,概率的频率定义是不够严谨的。
3.统计定义
在一定条件下,重复做n次试验,nA为n次试验中事件A发生的次数,如果随着n逐渐增大,频率nA/n逐渐稳定在某一数值p附近,则数值p称为事件A在该条件下发生的概率,记作P(A)=p。这个定义成为概率的统计定义。
在历史上,第一个对“当试验次数n逐渐增大,频率nA稳定在其概率p上”这一论断给以严格的意义和数学证明的是雅各布·伯努利(Jacob Bernoulli)。
从概率的统计定义可以看到,数值p就是在该条件下刻画事件A发生可能性大小的一个数量指标。
由于频率nA/n总是介于0和1之间,从概率的统计定义可知,对任意事件A,皆有0≤P(A)≤1,P(Ω)=1,P(Φ)=0。其中Ω、Φ分别表示必然事件(在一定条件下必然发生的事件)和不可能事件(在一定条件下必然不发生的事件)。(www.chuimin.cn)
4.公理化定义
柯尔莫哥洛夫于1933年给出了概率的公理化定义,如下:
设E是随机试验,S是它的样本空间。对于E的每一事件A赋于一个实数,记为P(A),称为事件A的概率。这里P(·)是一个集合函数,P(·)要满足下列条件:
1)非负性:对于每一个事件A,有P(A)≥0;
2)规范性:对于必然事件Ω,有P(Ω)=1;
3)可列可加性:设A1,A2.是两两互不相容的事件,即对于i≠j,Ai∩Aj=φ,(i,j=1,2.),则有P(A1∪A2∪.)=P(A1)+PA2)+.
选择“概率”,弹出如图9-35所示的“概率”子选板,下面介绍几种概率函数VI。
图9-35 “概率”子选板
1.累积分布函数(连续)VI
计算连续累积分布函数(CDF)或随机方差x的值小于等于x的概率,x为选定分布的类型。必须手动选择所需要的多态实例,如图9-36所示。
2.逆累积分布函数(连续)VI
该VI计算各种分布的连续逆累积分布函数(CDF),节点如图9-37所示
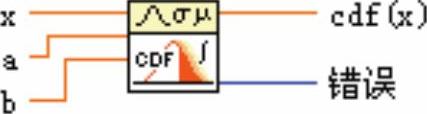
图9-36 累积分布函数(连续)VI节点
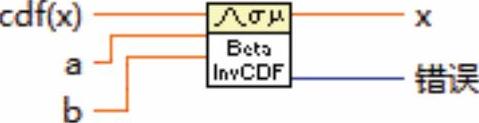
图9-37 逆累积分布函数(连续) VI节点
有关LabVIEW 2015虚拟仪器程序设计的文章

虚拟内存可用于运行较为大型的应用程序,但不适于时间条件苛刻的应用程序。有些情况下,可能会出现更少的运行时内存使用。并且,如果VI前面板或程序框图的规模超过了屏幕可显示的范围,将其分为子VI更便于其使用。特定的程序框图可阻止LabVIEW重复使用数据缓冲区。在子VI中通过一个条件显示控件能阻止LabVIEW对数据缓冲区的使用进行优化。......
2023-11-07

图2-2 “图标编辑器”对话框该对话框包括以下部分。“图标编辑器”对话框可显示LabVIEW Data\Glyphs中所有的.png、.bmp和.jpg文件。如使用编辑工具时单击左键,LabVIEW将使用线条颜色工具。如需创建自定义编辑环境,可修改“图标编辑器”对话框。创建自定义图标编辑器时,可使用labview\resource\plugins\IconEditor\Discover Who Invoked the Icon Editor.vi目录中的“搜索图标库调用方”VI获取当前编辑项图标的名称、路径和应用程序引用。......
2023-11-07

下面介绍如何在一个主VI中调用子VI,具体步骤如下。2)将子VI的图标放置在主VI程序框图窗口中。图4-63 “函数”选板图4-64 “选择需打开的VI”对话框3)用连线工具将子VI的各个连线端口与主VI的其他节点按照一定的逻辑关系连接起来。图4-67 “自定义窗口外观”对话框选中“调用时显示前面板”后,当程序运行到这个子VI时,其前面板就会自动弹出来。......
2023-11-07

拟合VI用于进行曲线拟合的分析或回归运算,拟合函数如图9-27所示。图9-27 “拟合”子选板1.线性拟合 VI线性拟合 VI表示通过最小二乘法、最小绝对残差或Bisquare方法返回数据集的线性拟合。将错误连接至“错误代码至错误簇转换”VI,可将错误代码或警告转换为错误簇。VI可以查找最佳拟合观测的a、b和c的值。下列等式用于描述由指数拟合算法得到的指数曲线:y[i]=aebx[i]+c图9-29 指数拟合VI......
2023-11-07

如图5-1所示,For循环有两个端口,总线接线端(输入端)和计数接线端(输出端)。如通过For循环处理大量计算,可启用并行提高性能。LabVIEW可通过并行循环利用多个处理器提高For循环的执行速度。通过查找可并行循环结果窗口确定可并行的For循环。通过For循环的并行实例接线端可指定运行时的并行实例数量。......
2023-11-07

程序框图提供VI的图形化源程序。在流程图中对VI编程,以控制和操纵定义在前面板上的输入和输出功能。图1-19 框图演示程序的程序框图1)节点:是程序框图上的对象,具有输入、输出端,在VI运行时进行运算。在程序框图中可将前面板的输入控件或显示控件显示为图标或数据类型接线端。Express VI是在配置对话框中配置的。......
2023-11-07

如果将字符串转换为数值,LabVIEW仅可以转换用于表示数值的字符串,而仍将其余值保存为字符串。同样由于浮点算术运算可能存在四舍五入误差,因此浮点数不能作为选择器标签的值,若将一个浮点数连接到条件分支,LabVIEW将对其舍入到最近的偶数值。图5-43 求平方根的程序框图分支1图5-44 求平方根的程序框图分支2图5-45 显示错误LabVIEW的条件结构与其他语言的条件结构相比,简单明了,结构简单,不但相当于Switch语句,还可以实现if…......
2023-11-07

图8-94 波形测量VI1.基本平均直流-均方根该项功能从信号输入端输入一个波形或数组,对其加窗,根据平均类型输入端口的值计算加窗口信号的平均直流及均方根。该测量通常与要求幅度和相位信息的高级测量配合使用。......
2023-11-07
相关推荐