首页理论教育内插与外推VI多种插值方法解析

内插与外推VI多种插值方法解析

2023-11-07 理论教育版权反馈

【摘要】：内插与外推VI可以用于进行一维和二维插值、分段插值、多项式插值和傅里叶插值如图9-30所示。图9-31 一维插值 VI节点下面介绍各输入、输出端选项含义。如果xi输入端已连线，则该VI将忽略n次。将错误连接至“错误代码至错误簇转换”VI，可将错误代码或警告转换为错误簇。该VI可提供5种不同的插值方法。图9-32 “多项式插值 VI”节点图9-33 “样条插值VI”节点在区间[xi,xi+1]，下列等式为输出插值y。

内插与外推VI可以用于进行一维和二维插值、分段插值、多项式插值和傅里叶插值如图9-30所示。

图9-30 “内插与外推”子选板

1.一维插值VI

通过选定的方法进行一维插值，方法由X和Y定义的查找表确定，该VI节点如图9-31所示。

图9-31 一维插值 VI节点

下面介绍各输入、输出端选项含义。

方法：指定插值方法。

1）最近—选择与当前xi值最接近的X值对应的Y值。LabVIEW在最近的数据点设置插值。

2）线性—设置连接X和Y数据点的线段上的点的插值。

3）样条—保证在数据点上三次插值多项式的一阶和二阶导数也是连续的。

4）cubic Hermite—保证三次插值多项式的一阶导数是连续的，设置端点的导数为特定值可保持Y数据的形状和单调性。

5）拉格朗日—使用重心拉格朗日插值算法。

Y：指定由因变量值组成的数组。

X：指定由自变量值组成的数组。X的长度必须等于Y的长度。

xi：指定由自变量值组成的数组，LabVIEW在这些自变量的位置计算插值yi。

X为单调变化：指定X中的值是否随索引单调增加。如果X为单调变化的值为TRUE，插值算法可避免对X进行排序，也可以避免重新对Y排序。如果X为单调变化的值为FALSE，VI将按照升序排列输入数组X并对Y排序。

n次：确定插值xi的位置，得到当xi为空时，每个Y元素之间的插值。Y元素之间的插值被重复n次。如果xi输入端已连线，则该VI将忽略n次。

yi：返回插值的输出数组，插值与xi自变量值相对应。

使用的xi：是因变量yi的插值待计算时，自变量值的一维数组。如果xi为空，则使用的xi返回(2n–1)*(N–1) + N个点，(2n–1)个点均匀分布在X中相邻两个元素之间，N是X的长度。如连线xi输入，VI将忽略n，使用的xi等于xi。

错误：返回VI的任何错误或警告。将错误连接至“错误代码至错误簇转换”VI，可将错误代码或警告转换为错误簇。该VI的输入为因变量Y和自变量X，输出与xi对应的插值yi。该VI查找X中的每个xi值，并使用X的相对地址查找Y中同一相对地址的插值yi。

该VI可提供5种不同的插值方法。

（1）最近方法

该方法用于查找最接近X中xi的点，然后使对应的y值分配给Y中的yi。

（2）线性方法

如果xi在X中两个点(xj,xj+1)之间，该方法在连接(xj,xj+1)的线段间进行插值yi。

（3）样条方法(www.chuimin.cn)

该方法为三次样条方法。通过该方法，VI可得出相邻两点间隔的三阶多项式。多项式满足下列条件。

在xj点的一阶和二阶导数连续。

多项式满足所有数据点。

起始点和末尾点的二阶导数为0。

（4）Cubic Hermite方法

三次Hermitian样条方法是分段三次Hermitian插值。通过该方法可以得到每个区间的Hermitian三阶多项式，且只有插值多项式的一阶导数连续。三次Hermitian方法比三次样条方法有更好的局部属性。如果更改数据点x_j，对插值结果的影响在[x_j–1,x_j]和[x_j,x_j+1]

（5）拉格朗日方法

通过该方法可得到N–1多项式，它满足X和Y中的N个点，N是X和Y的长度。该方法是对牛顿多项式的重新表示，可避免计算差商。下列方程为拉格朗日方法：

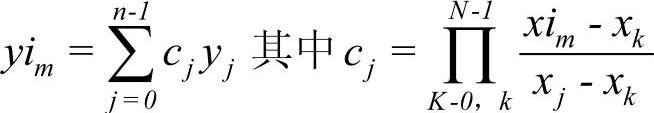
下列方法有助于选择适当的插值方法

最近方法和线性方法最简单但在多数应用中精度不能满足要求。

样条方法返回的结果最平滑。

三次Hermite的局部属性优于样条方法和拉格朗日方法。

拉格朗日方法宜于应用但不适用于应用计算。与样条方法相比，拉格朗日方法得到的插值结果带有极限导数。

2.多项式插值 VI

给定点集(x[i]y[i])，在x处对函数f进行内插或外插，f(x[i])=y[i]，f为任意函数，x值为给定值。VI计算输出的插值 P[n–1](x)，P[n–1]是满足点n(x[i]y[i])的阶数为n–1的唯一多项式。VI节点如图9-32所示。

3.样条插值 VI

返回x值的样条插值，给定(x[i], y[i])和通过样条插值VI得到的二阶导数插值。点由输入数组X和Y确定。VI节点如图9-33所示。

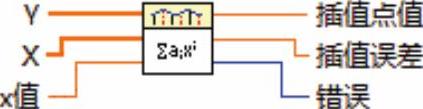
图9-32 “多项式插值 VI”节点

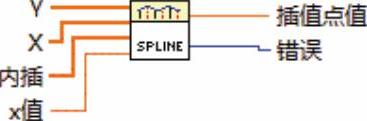
图9-33 “样条插值VI”节点

在区间[x_i,x_i+1]，下列等式为输出插值y。

y=Ay_i+By_i+1+Cy＂i+Dy＂i+1

其中