首页理论教育LabVIEW2015虚拟仪器程序设计：拟合VI分析曲线回归

LabVIEW2015虚拟仪器程序设计：拟合VI分析曲线回归

2025-09-30 理论教育版权反馈

【摘要】：拟合VI用于进行曲线拟合的分析或回归运算，拟合函数如图9-27所示。图9-27 “拟合”子选板1.线性拟合 VI线性拟合 VI表示通过最小二乘法、最小绝对残差或Bisquare方法返回数据集的线性拟合。将错误连接至“错误代码至错误簇转换”VI，可将错误代码或警告转换为错误簇。VI可以查找最佳拟合观测的a、b和c的值。下列等式用于描述由指数拟合算法得到的指数曲线：y[i]=aebx[i]+c图9-29 指数拟合VI

所谓拟合是指已知某函数的若干离散函数值{f1,f2,.,fn}，通过调整该函数中若干待定系数f（λ1, λ2,.,λn），使得该函数与已知点集的差别（最小二乘意义）最小。如果待定函数是线性，就叫作线性拟合或者线性回归（主要在统计中），否则叫作非线性拟合或者非线性回归。表达式也可以是分段函数，这种情况下叫作样条拟合。

拟合以及插值还有逼近是数值分析的三大基础工具，通俗意义上它们的区别在于：拟合是已知点列，从整体上靠近它们；插值是已知点列并且完全经过点列；逼近是已知曲线，或者点列，通过逼近使得构造的函数无限靠近它们。

拟合VI用于进行曲线拟合的分析或回归运算，拟合函数如图9-27所示。

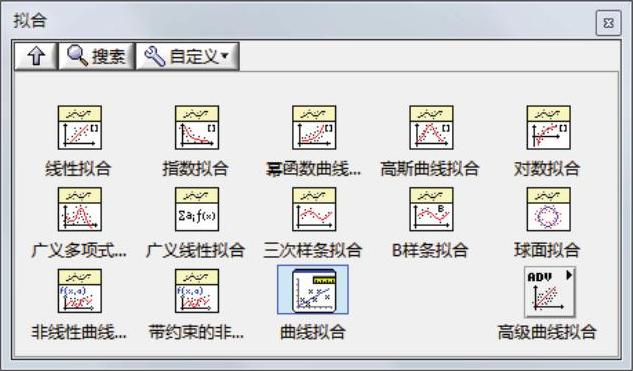
图9-27 “拟合”子选板

1.线性拟合 VI

线性拟合 VI表示通过最小二乘法、最小绝对残差或Bisquare方法返回数据集(X, Y)的线性拟合。

该VI通过循环调用广义最小二乘方法和Levenberg-Marquardt方法使实验数据拟合为下列等式代表的直线方程一般式：

f=ax+b

x是输入序列X，a是斜率，b是截距。该VI将得到观测点(X, Y)的最佳拟合a和b的值。

下列等式用于描述由线性拟合算法得到的线性曲线：

y[i]=ax[i]+b

该VI节点如图9-28所示。

下面介绍各输入、输出端选项含义。

Y：由因变值组成的数组。Y的长度必须大于等于未知参数的元素个数。

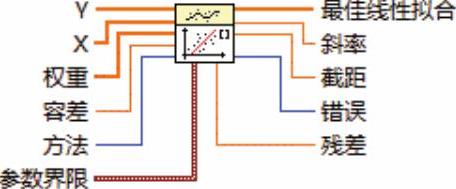
图9-28 函数节点

X：由自变量组成的数组。X的元素数必须等于Y的元素数。 (https://www.chuimin.cn)

权重：观测点(X, Y)的权重数组。权重的元素数必须等于Y的元素数。权重的元素必须不为0。如果权重中的某个元素小于0，VI将使用元素的绝对值。如果权重未连线，VI将把权重的所有元素设置为1。

容差：确定使用最小绝对残差或Bisquare方法时，何时停止斜率和截距的迭代调整。对于最小绝对残差方法，如果两次连续的交互之间残差的相对差小于容差，则该VI将返回结果残差。

参数界限：包含斜率和截距的上下限。如果知道特定参数的值，可以设置参数的上下限为该值。

最佳线性拟合：返回拟合模型的Y值。

斜率：返回拟合模型的斜率。

截距：返回拟合模型的截距。

错误：返回VI的任何错误或警告。将错误连接至“错误代码至错误簇转换”VI，可将错误代码或警告转换为错误簇。

残差：返回拟合模型的加权平均误差。如果方法设为最小绝对残差法，则残差为加权平均绝对误差。否则残差为加权均方误差。

2.指数拟合VI

通过最小二乘法、最小绝对残差或Bisquare方法返回数据集(X, Y)的指数拟合，如图9-29所示。

该VI通过循环调用广义最小二乘方法和Levenberg-Marqu ardt方法使数据拟合为通用形式由下列等式描述的指数曲线：

f=ae^bx+c

x是输入序列X，a是幅值，b是衰减，c是偏移量。VI可以查找最佳拟合观测(X, Y)的a、b和c的值。

下列等式用于描述由指数拟合算法得到的指数曲线：

y[i]=ae^bx[i]+c

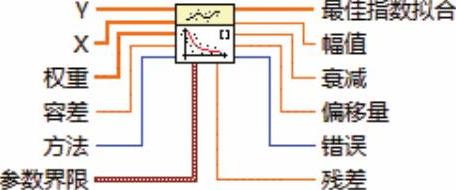
图9-29 指数拟合VI