LabVIEW2015：学习指数函数与对数函数

2023-11-07 理论教育版权反馈

【摘要】：本文最初集中于带有底数为欧拉数e 的指数函数，如图9-6所示。图9-6 指数函数图9-7 “底数为x的对数”函数

该类函数用于计算指数函数与对数函数，如图9-4所示。

1.指数函数

以指数为自变量底数为大于0且不等于1常量的函数称为指数函数，它是初等函数中的一种，如图9-5所示为指数函数。

指数函数是数学中重要的函数。应用到值e上的这个函数写为exp(x)。还可以等价的写为e^x，这里的e是数学常数，就是自然对数的底数，近似等于 2.718281828，还称为欧拉数。

当a＞1时，指数函数对于x的负数值非常平坦，对于x的正数值迅速攀升，在x等于 0 的时候，y等于1。当0＜a＜1时，指数函数对于x的负数值迅速攀升，对于x的正数值非常平坦，当x等于 0 的时候，y等于1。在x处的切线的斜率等于此处y的值乘上lna。即由导数知识得：

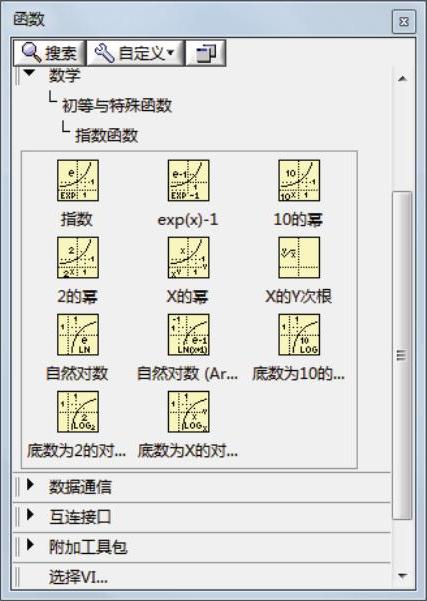
图9-4 “指数函数”子选板

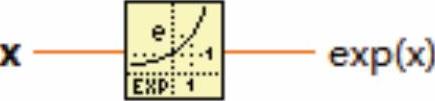
图9-5 指数函数

作为实数变量x的函数，

y=e^x 的图像总是正的（在x轴之上）并递增（从左向右看）。它永不触及x轴，尽管它可以无限程度地靠近x轴，所以，x轴是这个图像的水平渐近线。它的反函数是自然对数ln(x)，它定义在所有正数x上。

有时，尤其是在科学中，术语指数函数更一般性的用于形如(www.chuimin.cn)

k=a^x

（k属于R）的函数，这里的 a 叫作“底数”，是不等于 1 的任何正实数。本文最初集中于带有底数为欧拉数e 的指数函数，如图9-6所示。

指数函数的一般形式为

y=a^x

(a＞0且≠1) (x∈R)，从上面我们关于幂函数的讨论就可以知道，要想使得x能够取整个实数集合为定义域，则只有使得a＞0且a≠1。

2.对数函数

一般地，函数y=log_ax（a＞0，且a≠1）叫作对数函数，也就是说以指数为自变量，幂为因变量，底数为常量的函数，叫对数函数。

由于底数的特殊性，与对数相关函数底数为定值，对“底数为x的对数”函数，如图9-7所示。其中，如果y为0，输出为–∞。如果x和y都是非复数，且x小于等于0，或y小于0，输出为NaN。连线板可显示该多态函数的默认数据类型。

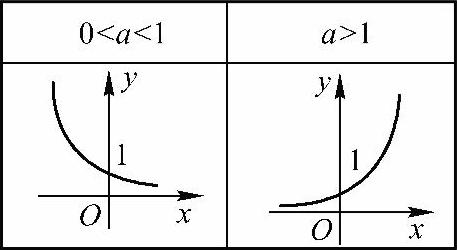
图9-6 指数函数

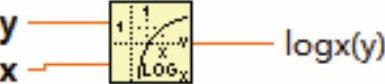
图9-7 “底数为x的对数”函数