首页理论教育地面灌溉优化灌水技术研究及实用手册-差分方程研究结果

地面灌溉优化灌水技术研究及实用手册-差分方程研究结果

2023-11-04 理论教育版权反馈

【摘要】：图6.1矩形计算单元体示意图截取如图6.2、图6.2 、图6.2 所示单元体，取计算时间步长为δt，考虑单元体上下游断面的空间权重系数和时间权重系数，将式（6.1）和式（6.2）所表示的连续方程和运动方程离散为差分方程:图6.2 是每个时段中组成右边界的推进峰单元；图6.2 是过渡单元，它是前一时段的推进峰作为起始时段，在确定的时间步长内变成矩形单元；图6.2 是位于推进峰之后的矩形单元。

pagenumber_ebook=111,pagenumber_book=104

图6.1　矩形计算单元体示意图

截取如图6.2（a）、图6.2 （b）、图6.2 （c）所示单元体，取计算时间步长为δt，考虑单元体上下游断面的空间权重系数和时间权重系数，将式（6.1）和式（6.2）所表示的连续方程和运动方程离散为差分方程:图6.2 （a）是每个时段中组成右边界的推进峰单元；图6.2 （b）是过渡单元，它是前一时段的推进峰作为起始时段，在确定的时间步长内变成矩形单元；图6.2 （c）是位于推进峰之后的矩形单元。

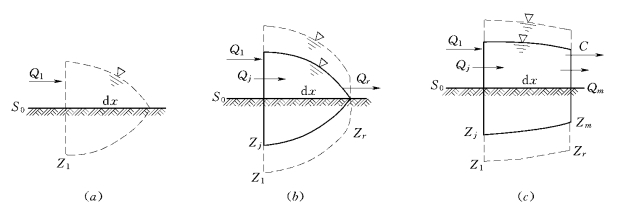
pagenumber_ebook=111,pagenumber_book=104

图6.2　截取单元体示意图

（a）推进峰单元；（b）过渡单元；（c）推进峰之后的矩形单元

在时间间隔ti-ti-1内，有以下关系式:

式中 δt——时段长度，δt=t i-ti-1 ；

θ——时间权重系数，是考虑计算时段起始和终了时刻在其平均值计算中所占的比重。

在时段Δt内，单元体内水量变化是:

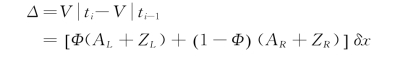
pagenumber_ebook=111,pagenumber_book=104

式中 δx——单元体长度；

A——水流断面面积；

Z——单位长度的入渗量；

Φ——空间权重系数，是考虑单元体上、下游断面在其平均值计算中所占的权重。由式（6.24）与式（6.25）相等可得运动波模型的连续性方程:

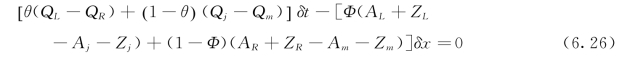
pagenumber_ebook=112,pagenumber_book=105

式中 δx——计算时段水流推进的距离增量；(www.chuimin.cn)

δt——时间步长；

A L、QL、Z L——时间t i时刻单元体左边界过水断面面积、流量和对应时刻的入渗量；

A R、QR、ZR——时间t i时刻单元体右边界过水断面面积、流量和对应时刻的入渗量；

A j、Qj、Zj——时间t i-1时刻单元体左边界过水断面面积、流量和对应时刻的入渗量；

Am、Qm、Zm——时间t i-1时刻单元体右边界过水断面面积、流量和对应时刻的入渗量；

Φ——空间权重系数，若上游断面权重系数为Φ，则下游断面权重系数为1-Φ；

θ——时间权重系数，若起始时刻ti-1的权重系数为θ，则终了时刻权重系数为1-θ。

Φ 和θ 值是一个能够反映隐式差分格式稳定性和灵活性的重要系数，一般取值在0.6～1.0之间为宜。通常取Φ=0.5，θ=0.6。

在编程过程中，初始条件给出了Qj和Q L，应用公式:

pagenumber_ebook=112,pagenumber_book=105

就可以相应求得A j和A L，同样用上三式把QR用A R表示，则连续方程变为:

pagenumber_ebook=112,pagenumber_book=105

式中 2≤k＜N-1。

对于推进峰单元，j、m、R 的流量Q 和水深A 均为0，连续方程简化为

式中 θ和Φ——流体单元瞬时变化的平均值。

由于A L能从前边单元中求得，Z L是时间的独立函数，则未知的δx N 可求出: