土壤入渗能力预测模型建立：地面灌溉优化与实用手册

2025-09-30 理论教育版权反馈

【摘要】：图5.21多元线性回归预测模型流程图经过大量分析，回归模型的显著性较好的各种变量组合如表5.6所示，各种预测模型回归参数估计及检验见表5.7。所以，经过分析，取模型Ⅶ作为该区域土壤入渗能力的预测模型。

根据南郊区试验资料和第5.1节的分析结果可知，影响土壤入渗能力的主要因素有土壤质地、不同耕作措施、土壤含水量、土壤有机质含量，其选取的自变量为:有机质含量0～20cm，土壤干容重0～10cm、10～20cm、0～20cm，土壤物理性粘粒含量（＜0.01mm）0～20cm，砂粒0～20cm、20～40cm、0～40cm，粉粒0～20cm、20～40cm，土壤含水量0～2cm、2～10cm、10～20cm、0～20cm、20～30cm；其他非主要因素的影响都包含在β0中。

根据南郊区40组大田土壤入渗试验资料，选取不同的变量进行组合，利用式（5.4）的多元线性回归模型，对南郊区的土壤入渗能力进行预测，并对以上各个变量的各种组合进行回归模型和回归模型系数的显著性分析，确定最佳的各种变量组合和最佳的土壤入渗预报模型。如果回归模型不显著，说明这种变量组合与各变量的回归是不显著的。如果回归系数不显著的因素，说明其对土壤入渗能力的影响较小，可暂不考虑。多元线性回归预测模型流程图见图5.21。

pagenumber_ebook=90,pagenumber_book=83

图5.21　多元线性回归预测模型流程图

经过大量分析，回归模型的显著性较好的各种变量组合如表5.6所示，各种预测模型回归参数估计及检验见表5.7。

表5.6　各种模型的变量组合

pagenumber_ebook=90,pagenumber_book=83 (https://www.chuimin.cn)

表5.7　各种变量组合的土壤入渗能力预报模型参数估计及检验表

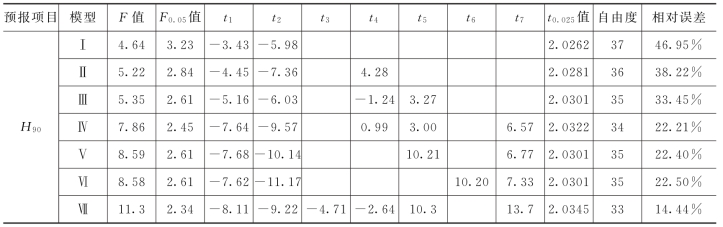
pagenumber_ebook=90,pagenumber_book=83

如表5.7所示，七个模型所计算的F 值都大于相应的F 0.05值，且相差幅度较大，说明七个预测模型都是显著的；根据试验观测值计算t值和给定显著水平α=0.05查得tα/2的值比较可知，模型Ⅰ、模型Ⅱ、模型Ⅴ、模型Ⅵ、模型Ⅶ中所选变量对H 90值的影响都是显著的。模型Ⅲ、模型Ⅳ中只有砂粒0～20cm 对H 90值的影响不显著，其他几个变量对其影响都是显著的。从预测误差分析可知，随着变量个数的增加，相对误差减小，说明考虑的影响因素越多，预测结果越准确。模型Ⅳ的预测误差较小，但有一个变量（t 3）不显著；模型Ⅴ的预测误差也小，各变量的显著性好，但其中的一个变量是20～40cm 砂粒含量，说明土壤入渗能力与表层0～20cm 砂粒含量无关，而与20～40cm 土层的砂粒含量有关。这与实际情况不太符合；模型Ⅵ和模型Ⅶ的各因素的显著性都很好，但模型Ⅶ预测误差比模型Ⅵ的误差小，各变量对其影响的显著性较好。所以，经过分析，取模型Ⅶ作为该区域土壤入渗能力的预测模型。该模型各变量回归参数估计见表5.8。

表5.8　模型Ⅶ土壤入渗能力预报模型参数表

pagenumber_ebook=91,pagenumber_book=84

土壤入渗能力预测模型建立：地面灌溉优化与实用手册

相关推荐