但是新诗的发展并没有因为形式上的反传统而彻底地与母体文化决裂。这被称作第二次新诗的生成，它有着对传统比兴——以物起情和随物婉转的诗歌创作和表现的复归。但是由于国人的感兴表达习惯和抽象思维的训练不足导致这种直接的抽象理念叙述或者纯粹的写景写实的新诗发展并不理想。......
2023-11-30
地面灌溉优化：土壤含水量对其影响研究
【摘要】：土壤初始含水量是影响土壤入渗能力的主要因素之一。土壤含水量主要从入渗水流湿润区内的平均势梯度方面影响土壤水分的入渗能力。图5.2为古店村田块3种不同土壤结构状态下，不同含水量水平的累积入渗曲线。经验入渗系数k值随着土壤含水量的增加而减小，较好的符合对数关系。在相同的土壤质地和结构条件下，由于土壤水势是土壤含水量的函数，所以土壤含水量将成为影响k值大小的唯一因素。
土壤初始含水量是影响土壤入渗能力的主要因素之一。土壤含水量主要从入渗水流湿润区内的平均势梯度方面影响土壤水分的入渗能力。土壤含水量 （占土重的百分数表示）指的是表层0～20cm 的平均含水量。下面以大同市南郊区古店镇古店村的试验数据为依据，来分析土壤初始含水量对土壤入渗特性的影响。
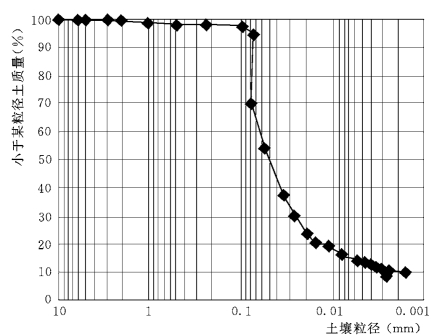
图5.1 南郊区古店村0～20cm 颗粒级配曲线
1.土壤入渗能力与土壤含水量的关系
古店村土壤质地为壤土，其中土壤表层0～20cm 的砂粒含量为47.82%，粉粒含量为44%，粘粒含量为8.1%，土壤物理性粘粒含量为19.2%，土壤颗粒级配曲线见图5.1；土壤表层0～20cm 的有机质含量为0.74%；不同耕作条件下的表层0～20cm 土壤干容重分别是:原茬地1.256g/cm3、犁耕翻松地1.104g/cm3、犁耕压实地1.167g/cm3。
图5.2为古店村田块3种不同土壤结构状态下，不同含水量（占干土重量的百分数表示）水平的累积入渗曲线。图5.2 （a）为原茬地在不同初始土壤含水量条件下的土壤水分累积入渗曲线。当土壤含水量由11.2%增加到29.6%时，土壤H 90由6.66cm 减小到2.428cm。图5.2 （b）和图5.2 （c）分别为翻松地和压实地不同土壤含水量下的土壤水分累积入渗曲线。
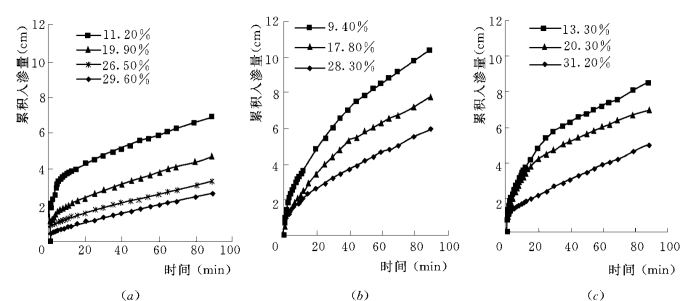
图5.2 不同土壤含水量下的土壤累积入渗曲线
（a）原茬地；（b）翻松地；（c）压实地
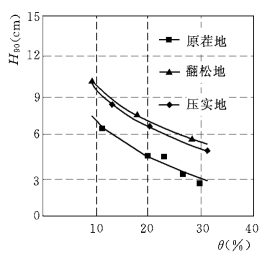
图5.3 H 90随土壤含水量变化曲线
在图5.2 （b）情况下，当土壤含水量在9.4%～28.3%之间变化时，土壤H 90在5.723～10.143cm 之间变化；图5.2 （c）情况下，当土壤含水量在13.3%～31.2%之间变化时，土壤H 90 在8.32～4.738cm 之间变化。结果表明，在同一土壤质地、土壤有机质含量相同条件下，土壤含水量对大田土壤入渗能力的影响十分明显，不论土壤耕作条件如何，都有随着初始土壤含水量的增高，土壤水分累积入渗量下降。
如图5.3所示的三条曲线分别为古店村原茬地、翻松地和压实地的H 90随土壤含水量变化曲线。由图5.3可以看出:无论是哪种土壤耕作状况，其H 90随着土壤含水量的增大而减小，都具有相同的变化趋势。即同样土壤质地条件下，土壤入渗能力随着土壤含水量的增大而减小。
如图5.3所示的拟合曲线表明，土壤90min累积入渗量与土壤含水量之间的关系符合对数函数，且相关性比较好。三种土壤结构状态下拟合方程如下（0%＜θ＜35%）:
原茬地:H 90=-4.1723lnθ+16.91，R=0.9733
翻松地:H 90=-4.0136lnθ+19.127，R=0.9999
压实地:H 90=-4.2023lnθ+19.265，R=0.9977
土壤入渗过程是非饱和土壤水分的运动过程，属于广义渗流理论的研究范畴，其基础为法国工程师Darcy提出的达西定律。Darcy （1856）通过饱和砂层的渗透试验，得出通量q和水力梯度成正比，即达西定律:
式中 L——渗流路径的直线长度；
ΔH——渗流路径始末断面总水头差；
ΔH/L——相应的水力梯度；
K s——饱和导水率。
Richards（1931）将达西定律引入非饱和土壤水流动为:
式中 K（θ）——非饱和导水率，又叫水力传导度；
∇ψ——总水势梯度。
式（5.2）成为研究非饱和土壤水流动的基本定律。
根据上述式（5.2）可知，决定入渗量大小的主要因素是土水势梯度和水力传导度。土壤含水量主要从入渗水流湿润区的平均势梯度方面影响土壤水分入渗能力。土壤初始含水量越高，水分入渗锋面的土水势越高，则水分入渗锋面与地表之间的平均势梯度越小，因此土壤的入渗通量越小，即土壤入渗能力越低。
2.土壤入渗模型参数与土壤含水量间的关系
目前对于土壤水分入渗过程的描述，人们应用较多的模型是以Kostiakov 和(www.chuimin.cn)
Kostiakov
Lewis公式，本书采用的土壤入渗模型是Kostiakov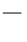
Lewis入渗公式:
式中 I（t）——累积入渗量；
k——入渗系数；
α——入渗指数，k和α 由试验资料回归分析得出；
f 0——相对稳定入渗率，cm/min由试验资料中最后进入稳定阶段的入渗率来确定。
Kostiakov Lewis入渗公式能够很好地预测入渗过程，特别是对于长历时入渗，较其他公式具有更高的预测精度。入渗模型的三个参数α、k 和f 0都有其一定的物理意义。k为经验入渗系数，其物理意义是入渗开始后第一个单位时段末的累积入渗量，在数值上也等于第一个单位时段末的入渗速度；α 为经验入渗指数，反映土壤入渗能力的衰减速度；f 0为土壤的相对稳定入渗率，即单位势梯度下饱和土壤的入渗速度，即非饱和土壤入渗速度达到相对稳定时的入渗速度。根据古店村的试验资料，来分析土壤含水量对经验模型三个参数的影响，以便为大田土壤入渗能力的预测提供依据。
（1）经验入渗系数k与土壤含水量的关系。图5.4为古店村不同土壤耕作条件下经验入渗系数k与土壤含水量的关系曲线，结果表明:土壤含水量对经验入渗系数k的影响很明显，不同土壤耕作条件下的关系曲线都有相似的变化趋势，即随着含水量的增加而减小。经验入渗系数k值随着土壤含水量的增加而减小，较好的符合对数关系。三条曲线拟合方程如下:
原茬地:k=-0.7405lnθ+3.1269，R=0.8334
翻松地:k=-0.6872lnθ+2.6338，R=0.9498
压实地:k=-0.8182lnθ+3.7442，R=0.9499
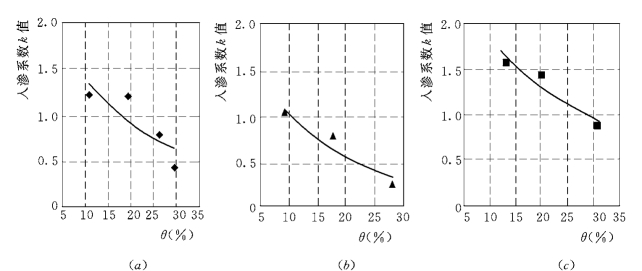
图5.4 k与θ 关系曲线 （0＜θ＜40%）
（a）原茬地；（b）翻松地；（c）压实地
土壤入渗模型参数k值是指入渗开始后1min时的入渗率或入渗量，是反映土壤入渗能力的一个重要指标。试验表明其值的大小与地表土壤的质地、结构、含水量和土壤水势有关。其原理是在开始入渗后的很短时间内，水分将使地表一定厚度内的土壤达到准饱和。在相同的土壤质地和结构条件下，由于土壤水势是土壤含水量的函数，所以土壤含水量将成为影响k值大小的唯一因素。其原因是:入渗初期的水分运动可以近似为饱和土壤中的水分运动（因地表一定厚度内的土层在入渗初期开始后很快饱和）。在过水面积一定的情况下，入渗通量取决于势梯度，而势梯度的大小主要取决于土壤含水量。在给定土壤质地和土壤结构的条件下，土壤含水量越高，其值越小，入渗通量也就越小。因此，土壤含水量越高，则k值越小。
（2）土壤含水量对经验入渗指数α的影响。图5.5为古店村不同土壤耕作条件下入渗指数α与土壤含水量的关系曲线，结果表明:土壤含水量对经验入渗指数α的影响比较明显，不同土壤耕作条件下的关系曲线都有相似的变化趋势，即随着含水量的增加而减小。经验入渗指数α值随着土壤含水量的增加而减小，较好的符合对数关系。三条曲线拟合方程如下:
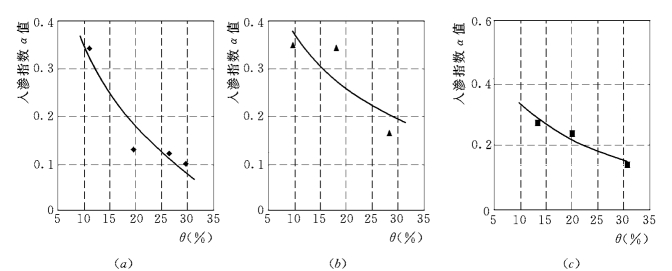
图5.5 α与θ 的关系曲线 （0＜θ＜40%）
（a）原茬地；（b）翻松地；（c）压实地
原茬地:α=-0.2501lnθ+0.9266，R=0.9556翻松地:α=-0.1615lnθ+0.7314，R=0.8352压实地:α=-0.1603lnθ+0.7020，R=0.9664
（3）土壤含水量对相对稳定入渗率的影响。图5.6为古店村不同土壤耕作条件下土壤入渗模型参数f 0与土壤含水量的关系曲线，结果表明:土壤含水量对f 0的影响也比较明显，不同土壤耕作条件下的关系曲线都有相似的变化趋势，即随着含水量的增加而减小。土壤入渗模型参数f 0随着土壤含水量的增加而减小，较好的符合对数关系。三条曲线拟合方程如下:
原茬地:f 0=-0.0392lnθ+0.1503，R=0.9825
翻松地:f 0=-0.0132lnθ+0.0871，R=0.9971
压实地:f 0=-0.0223lnθ+0.1029，R=0.9987
土壤入渗模型参数f 0是入渗达到相对稳定时的土壤水力传导度，也称饱和导水率。其大小与土壤质地、土壤初始含水量和土壤结构等因素有关，但主要取决于土壤孔隙的多少和大小。土壤孔隙越多，相应地稳定入渗率就大。由图5.6可以看出，翻松地的稳定入渗率相对原茬地和压实地来说是最大的，原茬地稳定入渗率较小。这是由于翻松地土壤孔
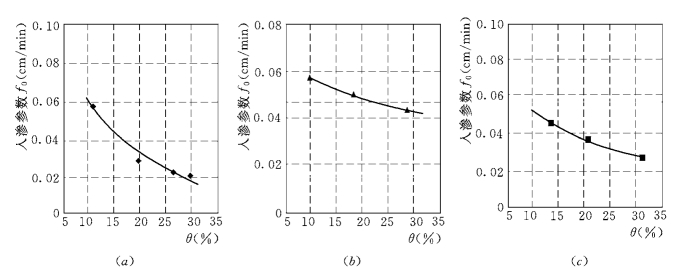
图5.6 f 0 与θ关系曲线 （0＜θ＜40%）
（a）原茬地；（b）翻松地；（c）压实地
隙比其他两种耕作状况的要多，土壤越疏松，土壤孔隙也就越多，孔隙率也越大，故土壤相对稳定入渗率f 0也越大。土壤原始含水量高，说明土壤中的孔隙相对地减少，则相应地稳定入渗率就低。
综上所述，通过试验数据分析表明，土壤含水量与土壤入渗能力与土壤入渗参数的关系都十分密切，土壤入渗能力及入渗参数都随着土壤含水量的增加而相应地减少，它们之间拟合的曲线符合对数关系。
有关地面灌溉优化灌水技术研究及实用手册的文章
- 详细阅读
-
地面灌溉优化：其他影响因素分析详细阅读
由于本次大田土壤入渗试验所用的水源是井水，含沙量甚小，所以研究暂不把含沙量作为独立影响因素考虑。疏松的表土在自然因素、人为因素和土壤自身特性的共同作用下会变的密实。因此，表土结皮也应作为影响大田土壤入渗能力的因素之一。灌溉在一定程度上破坏表土结构，并为耕层土壤的密实和地表的结皮创造条件，因此随着灌溉次数的增加，土壤水分入渗能力减小，尤其第一次灌溉对土壤水分入渗能力的影响大。......
2023-11-04
-
中日贸易现状及正德新令对其影响详细阅读
正德新令只规定了赴日唐船的船数和贸易总额，自然无法对清朝商人贩卖何种货物及货物的质量作出规定。谕文首先指责清朝赴日商人失信，谕令强调，正德新令采用信牌，分别港门，是为了便于贸易，而各地赴日的清商，所带货物雷同，未有各地特产之别。而正德新例使商船如期赴日也有一定难度。实行信牌制度后，唐船来年赴日，空闲一年，只好转往别处贸易，以致延误前往长崎的时日。......
2023-10-16
-
浓度梯度对热迁移影响的优化研究详细阅读
从动力学的观点来看，固溶体从均匀转变为不均匀的过程需要一个逆浓度梯度的上坡扩散，因此热迁移是逆浓度梯度的。值得注意的是，热迁移过程中，向热端扩散的元素既与温度梯度相反又与浓度梯度相反。与之对应，当建立起足够大的浓度梯度时，热迁移效应为零，即J＝0，那么浓度梯度将会是一个常数。当长度很长时，由于浓度梯度取决于均相固溶体的初始浓度，浓度梯度可能不会大到能够平衡热迁移的程度。......
2023-06-20
-
地面灌溉优化研究成果详细阅读
模型中的变量有两类，一类为被预测量；另一类为输入变量。本模型输入变量选择影响土壤入渗能力的主要因素。为了预报模型的准确性，本模型选择土壤0～20cm 和20～40cm 土层中的砂粒含量、粉粒含量、粘粒含量和0～20cm 土层内的物理性粘粒含量作为模型中土壤质地的变量。......
2023-11-04
-
溶剂浓度对溶胀工艺影响的优化研究详细阅读
由于水和NMMO的电负性不同，NMMO具有更强的与纤维素羟基形成氢键的能力，因此，当NMMO水溶液的浓度发生变化时，会对溶胀过程产生明显的影响。因此，通常认为要破坏纤维素大分子间氢键的NMMO溶液的浓度必须高于72%。许虎[2]等同样用溶胀后的浆粕经离心脱水后，测定浆粕质量的方法研究了在74%、76%和78%NMMO三种浓度下，浓度对溶胀性能的影响。结果发现，78%浓度的NMMO的溶胀性能明显的优于前两者。......
2023-06-25
-
地面灌溉土壤质地影响研究成果详细阅读
经分析比较认为，在分析土壤质地对土壤入渗能力的影响中，以d＜0.01mm 的物理性粘粒含量百分数作为反映土壤质地的物理量。由图5.13可以看出无论哪种耕作条件，参数k值随土壤物理性粘粒含量的增加而增加，也就是说，参数k值随土壤质地的变重而增加。在相同土壤结构和土壤含水量条件下，土壤质地和土壤水势将成为影响k值大小的主要因素。......
2023-11-04
-
中亚佛教：印度笈多朝对其影响的探讨详细阅读
印度佛教与希腊的美术思潮，几乎在同一时期传入中亚。但是纯印度的笈多派，却在之后的一段时间才传入。在戈壁以南地区，笈多派在公元8世纪才终于风靡于丹丹乌里克的壁画领域。□丹丹乌里克壁画残片戈壁沙漠的北部绿洲是特别的，它们直接受到了印度—笈多王朝的影响。从公元6世纪开始，笈多王朝艺术传入整个中亚，导致中亚的绘画风格开始发生转变。它展示出了伊朗艺术在突厥斯坦产生的影响。......
2023-07-03
相关推荐