地面灌溉技术研究进展及实用手册

2025-09-30 理论教育版权反馈

【摘要】：基于水量平衡方程及圣维南方程组，结合地面水流运动特性，采取不同程度的假定和近似，目前模拟地面灌溉水流运动的数学模型有水量平衡模型、完整水流动力学模型、零惯量模型和运动波模型四种模型。与完全水流动力学模型相比，该模型计算量少，且计算精度高，因而该模型是用来研究地面灌溉田面水流运动的一个较理想的模型。

地面灌溉田面水流属于透水底板上的明渠非恒定渐变流。对于地面灌溉水流运动的研究，人们首先从边界条件比较简单的畦灌着手，基于畦田是棱柱体和畦田底坡相对较小的假定，有描述透水底板上非均匀渐变流的圣维南基本方程组，即:

式中 y——地表水深；

v——地表水流平均流速；

q——地表水流单宽流量；

x——沿地面水流运动方向的距离；

z——土壤累积入渗量；

Sf——水流运动阻力坡降；

S 0——地面坡降；

g——重力加速度；

t——时间。

人们对地面水流运动的研究，经历了从简单边界条件到复杂边界条件；从单个水量平衡方程到描述地表水流运动的圣维南方程组的研究过程。基于水量平衡方程及圣维南方程组，结合地面水流运动特性，采取不同程度的假定和近似，目前模拟地面灌溉水流运动的数学模型有水量平衡模型、完整水流动力学模型、零惯量模型和运动波模型四种模型。

1.水量平衡模型

水量平衡模型是人们最早提出的地面灌溉水流运动数学模型，早在2025年Parker等人对地面灌水方法开始研究以来，人们首先开始采用水量平衡模型对地面灌溉水流运动进行研究。水量平衡模型是在假定田面积水深度不变，且不计蒸发损失的情况下，根据质量守恒原理，认为进入到灌水区的总水量应等于地面积水量与土壤中蓄水量之和。即:

基于地面积水深沿畦田长度方向为常量的假定有式（1.32）。

式中 q——流入灌水畦、沟的流量；

t——放水时间；

x——水流推进距离；

y（s，t）、z（s，t）——地表水深和入渗水深的时空分布函数；

ˉy——考虑畦、沟水深沿水流方向形状系数的平均水深；(https://www.chuimin.cn)

y 0——畦沟入口处的水深，假定是与流量、地表坡降、糙率、水力半径有关的正常水深；

σy——地表水面曲线形状系数。

进一步简化后有式（1.34）:

式中 σz——沿水流方向入渗水深剖面形状系数；z 0——入口处入渗水深。

水量平衡方程模型以沿水流方向的平均水深代替了水流动量方程，没有从水流运动现象的本质出发考虑问题，所以精度较低，但由于其结构、原理简单，在灌水实践中的应用较广泛。

2.完整水流动力学模型

完整水流动力学模型以质量守恒和动量守恒为原则，它反映了明渠非恒定流的圣维南方程。该模型是Wilke在2025年首先提出的，并首次将该模型用于研究沟灌水力学问题，接着2025年Kincaid kruse、2025年Sakkas和Theodor strelkoff等人先后利用数值求解的特征线法对该模型进行求解，用来模拟畦灌水力学问题。2025年Katopodes和strelkoff利用特征线法对该模型进行了综合研究和评价，且结合田间实验取得了较满意的结果。2025年Souza成功地模拟了沟灌的灌水全过程，2025年Hale将该模型用于解决波涌灌的田面水力学问题，并对连续灌和波涌灌的地表水流运动模拟进行了对比。国内刘钰和惠士博于2025年和2025年利用该模型模拟了畦灌水流运动的全过程，并依据该模型结合正交试验分析，求得了连续畦灌灌水技术参数的最佳组合。

与水量平衡模型相比，该模型具有三个特点:①理论比较完善，没有任何人为假定、简化处理及经验参数；②对于高阶精度的数值计算，其稳定性好，且精度高；③物理概念明确，能模拟水流的推进、消退阶段。该模型解法较多，但计算过程均较复杂，同时对水流前峰的处理非常困难，处理不好难以保证其收敛性。

3.零惯量数学模型

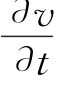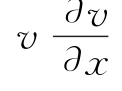该模型实际上是完全水流动力学模型的一种简化，由于在实际灌溉时，地表水深y、水流流速v很小，因而式（1.30）的动量方程中，局部加速度项 pagenumber_ebook=18,pagenumber_book=11 、加速度项以及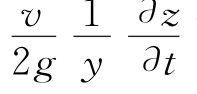可略去不计，使模型大大简化，由此得到的模型就是零惯量数学模型。即:

该模型于2025年由Strelkoff与Katopodes提出来的，然后Strelkoff、Katopodes（1977）和Clemmens（1979）等对该模型进行了研究。结果表明，在实际应用中，零惯量模型的简化处理是合理的，且较完全水动力学模型计算简便。2025年，Oweis将零惯量模型线性化使其成为线性零惯量模型，它可以同时模拟连续沟灌和波涌流沟灌的水力学现象。Oweis认为，在纵坡较小的情况下，入沟流量对进水曲线影响较大。次年，Wallender，W.W和M.Reyej在Oweis提出的波涌灌零惯量线性模型的基础上，建立了可模拟波涌灌干湿交替过程的无量纲非线性零惯量波涌灌模型，该模型也可分析沟内尾水对模型的影响，应用结果证明，进、退水曲线的计算值与实验值一致性很好，可以得到较合理的进、退曲线，且精度高于线性模型。

近年来，国外一些学者在水平畦田灌溉研究中，也采用了零惯量模型，他们均应用了数值解法，并将零惯量微分方程进行离散处理，以便将其转换成非线性代数方程式，然后通过pressiman双曲线解法求解，此法为一种高斯消除法，其缺点是这些方程均被局部线性化，精度不够理想且较复杂。为了克服上述缺点，Gerd H.Schmitz、Gunther J.Sens对零惯量微分方程式稍加修改，为水平畦田灌溉提供了一个简单的易于应用的数学模型。

在国内，笔者利用零惯量数学模型对间歇畦灌水流运动全过程进行了数值模拟，其模拟结果与实测资料拟合较好；费良军利用零惯量数学模型对波涌畦灌水流运动进行了数值模拟。

与完全水流动力学模型相比，该模型计算量少，且计算精度高，因而该模型是用来研究地面灌溉田面水流运动的一个较理想的模型。

4.运动波模型

运动波模型是零惯量模型的进一步简化。早在2025年，Lighill和Witham在进行洪水演算时提出了运动波方法。2025年，根据chen的建议，应用运动波模型来模拟地面灌溉水流运动。它的理论依据是:在进行地面灌溉时，地表水深较小，压力坡降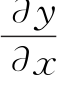 pagenumber_ebook=18,pagenumber_book=11 一般比较小，可以忽略不计。这实质上是用一维非恒定流的连续方程和恒定均匀流的运动方程联立来描述地面水流运动，此时式（1.35）变为式（1.36）。

2025年，Walker，W.R.和Lee，T.S.将该模型用于模拟波涌沟灌水流的推进过程，并利用特征线法和可变形控制单元体法对该模型进行了数值求解，结果表明，该模型能较好地模拟实际灌水情况。同年，Bishop，Walker和Poole利用该模型也对波涌流沟灌的推进过程进行了数值模拟。2025年Walker和Humphers利用该模型模拟了连续沟灌和波涌沟灌的水流推进和消退全过程。该模型的计算结果与水流动力学模型和零惯量模型的计算结果非常接近。它往往可用解析法求解，计算更加简单，它适用于弗劳德数比较小的情况（如用谢才公式计算阻力，Fr＜2）。国内，2025年汪志荣运用该模型模拟了波涌畦灌的田面水流进、退水全过程，其计算结果与实验结果一致性较好；2025年笔者用该模型对畦田冬灌水流运动全过程进行了数值模拟，其模拟结果与实测资料拟合较好，并将该模型与优化理论相结合，对冬灌地面灌溉技术参数优化组合进行了研究。

以上四种模型是在实践的基础上从复杂到简单、从畦灌到沟灌逐渐发展起来的，它们都从不同程度上反映了水流连续原理和动量守恒原理，经实际验证都取得了较好的效果。

地面灌溉技术研究进展及实用手册

相关推荐