图4.10断裂突水型式示意图张性断裂；压性断裂活化；断裂扩展因断裂富水、导水而发生突水事故的情形有三种，如图4.10所示。图4.10表示隧道揭露富水的张性断裂而发生突水事故。对突水围岩本构关系分析看出，突水前，作用在围岩上应力为总应力σij，其值远大于正常掘进时岩体之间接触作用应力，且突水区围岩多为弱化岩体，受软化、蠕变、松弛、弹性后效等作用影响，使围岩流变明显加大。......
2023-11-04
水工程地质缺陷加固技术-单孔灌浆堵水可靠性
【摘要】：灌浆堵水的目的是以灌浆孔为中心形成满足设计和规范标准要求的隔水帷幕。现在的问题是，单孔灌浆堵水是否可靠，导致灌浆堵水失败的直接原因是什么？全面考虑灌浆过程，绘制单孔裂隙灌浆堵水系统故障树如图8.3所示。为直接分析灌浆堵水的可靠性，考虑各基本事件的影响程度，绘出简化后的灌浆堵水成功树如图8.4所示。2）扩散半径可靠性X2。5）灌浆泵可靠性X5。1）初灌的可靠性。2）复灌的可靠性。
灌浆堵水的目的是以灌浆孔为中心形成满足设计和规范标准要求的隔水帷幕。
现在的问题是，单孔灌浆堵水是否可靠，导致灌浆堵水失败的直接原因是什么？通过灌浆，当时突水被堵住了是否就意味着隔水帷幕成功有效？
（1）灌浆工艺流程反映出灌浆实现的过程①。如图8.1所示，灌浆从“原材料”到“结石体”全部工艺流程反映了灌浆实现的全过程（见图8.2）。
（2）灌浆堵水“故障树（The failure tree）”划分。导致灌浆堵水失败的直接原因定为浆液未在岩体中凝胶和浆液凝胶后的失效两种，这实际上反映了灌浆过程中的失效（不能在岩体中完成灌浆）和灌浆结束后的失效（未达灌浆标准）两种情况，体现出灌浆的全过程。全面考虑灌浆过程，绘制单孔裂隙灌浆堵水系统故障树如图8.3所示。
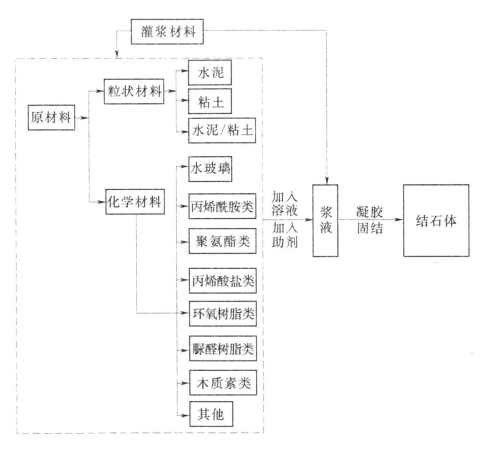
图8.1 灌浆材料凝胶/固结工艺流程框图
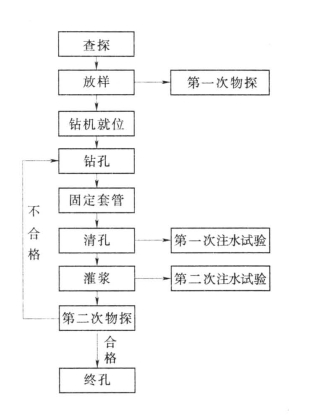
图8.2 灌浆施工全过程框图
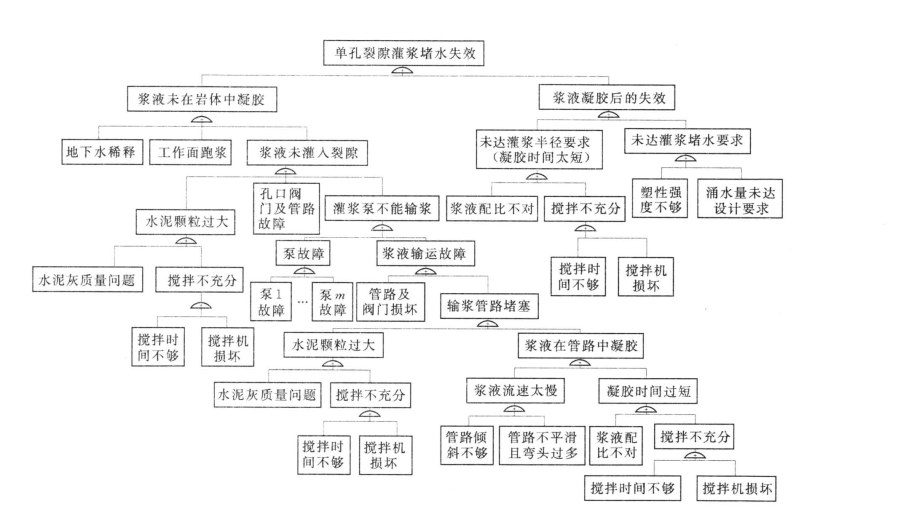
图8.3 单孔灌浆堵水系统故障树
该故障树对故障事件作了较细的划分，其中导致失效的基本事件包括：地下水的稀释，跑（冒）浆，水泥灰质量问题，搅拌时间不够，搅拌机损坏，各处阀门及管路故障，各灌浆泵故障，输浆管路倾斜不够及弯头过多，浆液配比未达要求，结石体未满足塑性强度，灌浆后涌水量未达要求等。
（3）绘制“成功树（The success tree）”。为直接分析灌浆堵水的可靠性，考虑各基本事件的影响程度，绘出简化后的灌浆堵水成功树如图8.4所示。成功树中逻辑门符号与故障树中所用逻辑门符号成对偶关系（与门变或门，或门变与门）。
图8.4 经简化的灌浆堵水成功树
此树简化中忽略了地下水稀释、跑浆、水泥灰质量、各处阀门及输浆管路、浆液配比等相对次要因素的影响。
（4）基本事件分析。可见，保证灌浆堵水成功（X）的基本事件有：水泥浆可灌入裂隙（X4）；灌浆泵运转正常（X5～X4+m，m为泵数）；扩散后达设计灌浆半径要求（X2）；凝胶体不被挤出（满足塑性强度要求）（X3）；涌水量达设计标准（X4）。其中X1、X3、X5、～、X4+m的目的是保证在岩体中灌浆的顺利实现；X2是保证达到灌浆半径要求，对灌浆堵水而言，是实现多孔灌浆时的灌浆交圈；Xi是保证达到现场开挖时的涌水量要求。
1）水泥浆可灌性Xl。水泥浆可灌性的计算，需根据不同水灰比W/C对应可灌入裂隙开度δ的实测结果进行回归，或参照有关资料，列出极限状态方程。
2）扩散半径可靠性X2。极限状态方程：
式中 R——灌浆半径设计值；
rc——灌浆孔半径；
K0——原岩渗透率；
L——灌浆段长；
pc——灌浆压力；
p0——静水压力；
Q——灌浆流量；
η——浆液动力粘度。
3）塑性强度可靠性X3。极限状态方程：
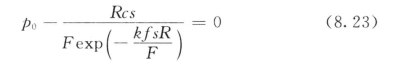
式中 c——凝胶体粘聚力；
k——侧压力系数；
f——摩擦系数；
s——裂隙周长；
F——裂隙截面积；
l——裂隙长度。
4）涌水量（残余水量）可靠性X4。
①灌浆前后的岩体渗透率（K0，K1）。灌浆后钻孔中仍有残余涌水是由于水泥浆液结石后体积收缩，即结石率的存在造成的。据结石率公式：α=（V0-V1）/V0，若设灌浆后裂隙（孔隙）被均匀充填，则得α=（V0-V1）/V0=1-δ1/δ0=1-m1/m0。(www.chuimin.cn)
据瓦赫拉梅耶夫公式：K=0.043m2.1δ2，可得灌浆前后的岩体渗透率关系：
式中 δ0、δ1——灌浆前、后裂隙开度；
m0、m1——灌浆前、后岩体孔隙率；
V0、V1——灌浆前、后孔隙体积；
Kn-1、Kn——第n次灌浆前、后岩体渗透率；
α——结石率。
②涌水量的极限状态方程。灌浆后的帷幕体渗透性与原岩渗透性相差很多，在计算地下水由灌浆帷幕外向钻孔渗透的涌水情况时，可以将帷幕外看作定水头（p=p0）边界向水头为零（p=0）的灌浆孔渗透，这是一个与灌浆相反的过程。据W=
，将式（8.24）代入，得初灌时的极限状态方程：
式中 η0——水的动力粘度；
W0——灌浆孔涌水量要求。
5）灌浆泵可靠性X5。
式中 Pas——可靠概率，Pas=1-m/M；
Pbs——维修性概率，Pbs=exp（-t/U）；
m——给定有效时间内故障发生次数；
M——给定有效时间内工作总次数；
U——维修周期；
t——维修时间。
（5）单孔灌浆系统的可靠性。
1）初灌的可靠性。由成功树可见各基本事件与顶事件（达到灌浆堵水一切要求）间的逻辑关系：
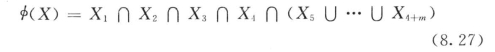
式中 φ（X）——X状态函数；
∩——逻辑串联符号；
∪——逻辑并联符号。
2）复灌的可靠性。一般来说，经过第一次灌浆后，由于结石率的影响，岩体裂隙不能全部封堵，灌浆难以达到要求。为此在现场施工中往往需要对同一孔进行多次扫孔重复灌浆，以进一步充填由于结石率的影响不能被完全充实的裂隙，才能达到灌浆标准。
定义n=1时，初灌；n=2时，第1次复灌；以此类推。第n次灌浆是指第n次灌浆本身的情况；第n次灌浆后是指经过n次灌浆后的情形，即历次灌浆形成的综合效果。
与初灌时推导过程类似，可得到第n次灌浆与第n-1次灌浆时裂隙开度及渗透率关系：
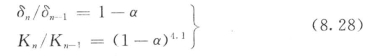
当某孔进行第n次灌浆时，是建立在第n-1次灌浆效果的基础之上，它的可靠性计算依赖于上次灌浆结果。第n次灌浆可靠性计算过程与第n-1次灌浆相同，但要注意到渗透率及孔隙度的变化。
第n次灌浆后，单孔灌浆系统要想达到可靠性要求，有两种情况：①第n-1次注浆结束后即可达到灌浆结束标准；②第n-1次灌浆顺利完成，但未达到涌水量要求，经进一步复灌后达到灌浆结束标准。由二者逻辑关系可知，复灌在逻辑上可看作是一种理想旁联系统。
设Xni为第n次灌浆时的Xi事件；Xnd为第n次灌浆达到灌浆标准的事件；Xns为第n次灌浆顺序实现、但未达涌水量标准的事件；Xne为第n次灌浆后达到灌浆标准的事件。则这几个事件的逻辑关系为
式中 φ（X（n-1）s）=X（n-1）1∩ X（n-1）2 ∩ X（n-1）3 ∩（X（n-1）5∪…∪ X（n-1）（4+m））∩（1-X（n-1）4）；φ（Xnd）=Xn1 ∩ Xn2 ∩ Xn3 ∩ Xn4∩（X（n-1）5 ∪…∪X（n-1）（4+m））。
又PX0d=PX0e，即初灌达到灌浆标准的概率与初灌后达到灌浆标准的概率相等。
有关水工程地质缺陷常用加固技术的文章
- 详细阅读
-
固结灌浆施工技术：水工程地质缺陷加固详细阅读
表8.7固结灌浆用细骨料级配表膨润土应于拌入浆液前经过24h的水化。2）固结灌浆作业。灌浆压力介于0.2～2.0MPa之间；视工况实际调整；⑥固结灌浆完成时的压力与时间表见表8.8；表8.8固结灌浆完成时的压力—时间关系表⑦化学浆材及化学灌浆的选用。当采用上述水泥固结灌浆尚需用化学浆材及化学灌浆作补灌，或者预先作水泥/化学复合固结灌浆时，应由雇主、监理工程师专门提出其固结灌浆施工设计报上级主管部门核批后进行；⑧固结......
2023-11-04
-
水工程地质缺陷常用加固技术：固结灌浆基础知识详细阅读
固结灌浆的概念与作用。1）当同一地段的基岩地质缺陷需进行防渗与加固灌浆时，必须以先固结灌浆后帷幕灌浆的顺序进行。2）固结灌浆宜在有混凝土覆盖的情况下进行。采用钻孔固结灌浆必须在相应部位的混凝土达到50%设计强度后，方可开始。5）固结灌浆孔应采用单点法压水试验在裂隙冲洗后进行，试验孔数不宜少于总孔数的5%。6）固结灌浆应按环间分序、环内加密的原则进行。8）固结灌浆孔围岩段长度小于6m时，可全孔一次灌浆。......
2023-11-04
-
水工程地质缺陷加固技术详细阅读
宏观上看，产生地质缺陷的力主要是地应力或以构造应力为主导的地应力。地应力总体上包括重力应力与构造应力两部分。即地质岩块吸水后发生湿胀而引起的应力。还有一点，构造应力是地球物理作用的结果，是不同力源产生同一性质的力——应力的综合力。......
2023-11-04
-
水工程地质缺陷常用加固技术详细阅读
2）当围岩局部发生塑性变形、不支护会塌方或产生变形破坏，以及完整的软岩时，须采用喷混凝土-系统锚杆加钢筋网；当地下洞室跨度在20～25m时，则须浇筑混凝土衬砌。表1.5地下洞室规模、围岩类别与锚喷支护及其参数表续表......
2023-11-04
-
水工程地质缺陷加固技术简介详细阅读
“占据一定三维空间范围的岩石和矿床的实体”称其为“地质体”，而“在地质体上或地质体内，以地质体作为建筑结构的工程”叫作“地质工程”。为此，在叙述水工程地质缺陷常用加固技术之前，有必要对地质缺陷的来龙去脉有个基本了解，以期为后述的加固技术作好铺垫。从工程地质角度看，影响水工程安全稳定的地质缺陷主要包括由构造运动产生的：①褶皱；②断层；③节理；④裂隙；⑤软弱破碎带；⑥泥化夹层。......
2023-11-04
-
水工程地质常用灌浆加固技术详细阅读
帷幕灌浆的概念与分类。帷幕灌浆设计的内容。帷幕灌浆使用的胶凝材料主要是水泥，特殊情况时使用高分子化学溶液，对砂砾石地基多用水泥粘土浆液。砂砾石层帷幕灌浆压力尽可能大些，以不引起地面抬动或虽有抬动但不超过允许值为限。在幕体中钻设检查孔进行压水试验是检查帷幕灌浆质量的主要手段，质量不合格的孔段要进行补灌，直至达到设计的防渗标准。帷幕灌浆主要施工方法。......
2023-11-04
-
水工程地质缺陷常用节理加固技术详细阅读
沿最大切应力方向发育的细而密集的剪切节理，称为“劈理”。图1.10根据节理产状与岩层产状关系的节理分类示意图图1.11根据节理产状与褶皱轴向关系的节理分类示意图另外，根据岩石的抗拉强度、岩石破裂面与最大主应力方向间的夹角关系，节理可分为三类：1）伸张节理，又称张力节理。图1.12中的C所示的混合节理，由岩石破裂时的有效轴差应力小于4～8倍岩石抗拉强度且最小有效主应力＜0的情况下所形成。......
2023-11-04
相关推荐