水工程地质缺陷加固技术-预应力锚杆案例

2023-11-04 理论教育版权反馈

【摘要】：闸室采用分离式底板，灌注桩基础。原设计每根灌注桩承担水平力300kN，校核情况每根承担440kN。针对防潮闸基础存在的软塑到流塑以及底板脱空现象，在水闸质量检测的基础上完成了基础加固的初步设计，其中一项重要的加固措施是对闸墩底板下的灌注桩辅以土层锚杆，用以解决闸室抗滑稳定不足的问题。预应力锚杆构造及加固闸基布置。图6.21为锚杆荷载随时间变化曲线。综合分析结果表明，宁车沽防潮闸基地质缺陷采用预应力土锚

（1）工程概述。宁车沽防潮闸位于天津市塘沽区宁车沽村西，潮白新河入永定新河处，是一座具有挡潮、蓄淡、泄洪、排沥等综合效益的大型水闸。该闸共22个闸孔，每孔净宽8m。闸室采用分离式底板，灌注桩基础。该闸自1971年建成以来，在防止潮水上溯减少河道淤积及槽蓄淡水等方面起到了重要作用，但是由于水闸长期在海洋及盐雾环境下运行，加上1976年唐山地震的破坏，使之存在诸多安全隐患。

闸底板脱空严重。从提供的资料及实际钻孔情况看，闸墩底板混凝土孔向厚度约2.7m，混凝土下局部存在5～8cm的脱空现象，在孔深8.0～8.5m以内为淤泥质软粘土层，强度很低呈软塑到流塑状态，钻孔进尺较快。另外，起阻滑板作用的上游防渗板和下游消力池底板存在脱空问题，因此其阻滑作用已大大降低。

防潮闸抗滑稳定不满足要求。原设计每根灌注桩承担水平力300kN，校核情况每根承担440kN。1996年水利部天津勘测设计院提交的《蓟运河、宁车沽防潮闸汛期和非汛期稳定复合报告》中根据现行规范，对宁车沽防潮闸灌注桩的水平允许承载力的核算表明其值不超过200kN。说明原设计单桩水平承载力取值偏高。原设计考虑水平力由阻滑板和灌注桩共同承担，校核情况下闸室本身的抗滑安全系数仅为0.46，远未达到现行规范规定的闸室本身抗滑稳定安全系数达到1.0的基本要求。

针对防潮闸基础存在的软塑到流塑以及底板脱空现象，在水闸质量检测的基础上完成了基础加固的初步设计，其中一项重要的加固措施是对闸墩底板下的灌注桩辅以土层锚杆，用以解决闸室抗滑稳定不足的问题。

（2）预应力锚杆构造及加固闸基布置。鉴于闸底板坐落的下卧地基由粘土、砂壤土和粉砂组成，其中粘土层3.1m厚、砂壤土3.0m厚，闸底板与粘土层脱空5～8cm的现实，研究决定采用土锚杆（索）加固闸基方案。

根据闸室稳定复核结果，考虑闸墩底板和原灌注桩基础设计情况，依据试验成果确定每根预应力锚杆设计轴向拉力为400kN，每块墩底板于闸墩两侧各布设4根锚杆，按对称于工作门槽布置，即每个闸墩底板主门槽前有4根倾向上游，主门槽后有4根倾向下游，倾角均为35°。每根锚杆长23m，其中上部自由段长4m，其余19m锚固于基础下粘土、砂壤土、粉砂土层中。锚索由7根钢绞线组成，每根钢绞线公称直径15.24mm，公称截面积140mm2，锚固浆体采用525号水泥特制的早强纯水泥浆液（抗盐蚀性能高），浆液比重为1.98，水灰比为0.38∶1，待一次注入的浆体初凝后，再进行二次注浆，直到达到设计要求。其作用原理为每根锚杆先预拉200kN，即储备与拉力方向相反的163.8kN水平阻滑力（即轴力）。闸墩无位移时因上、下游两侧预拉力对称，闸墩底板在预拉力作用下处于平衡状态。根据试验结果，一旦闸底板发生5mm位移，则受拉侧每根锚杆增加200kN轴力，实际受拉变为400kN，受压侧减少200kN轴向力，锚杆受力变为0，这样若主门槽一侧4根锚杆受到1600kN轴向力，则得到与位移反向的1311kN水平阻滑力，实现以锚杆抗滑的设计意图。锚杆的构造和布置分别见图6.17和图6.18。

（3）加固后的锚杆长期抗拔力与效果。

1）锚杆长期抗拔力分析估算。锚杆的长期抗拔力是评判加固效果的测度之一。因此，从布设锚杆到水闸运行期（一般为50年），锚杆不致因其蠕变（Creep）过度地降低抗拔力，使闸基失稳是衡量加固效果的举证。

研究表明，土层灌浆锚杆的蠕变力学模型可用Burgers模型表达（见图6.19）。

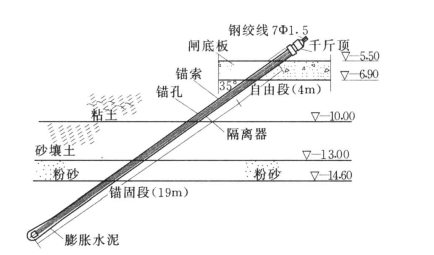
pagenumber_ebook=296,pagenumber_book=264

图6.17　锚杆构造图

pagenumber_ebook=296,pagenumber_book=264

图6.18　锚杆布置图

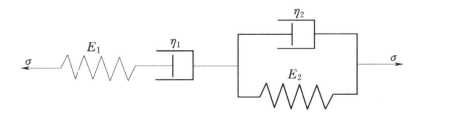
pagenumber_ebook=296,pagenumber_book=264

图6.19　Burgers模型

Burgers模型中粘壶元件的粘滞系数η1反映了在恒应变状态下的应力松弛现象，η1愈小，松弛时间愈短，应力衰减愈快；反之，η1愈大，松弛时间愈长，应力衰减愈慢，若η1→∞，则无任何蠕变变形发生。

由图6.19可见，Burgers模型由Maxwell体与Kelvin体组成。

经过数学推导，求出Burgers模型的蠕变方程^[7]：

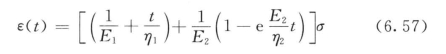
pagenumber_ebook=297,pagenumber_book=265

式中　ε（t）——蠕变位移；

σ——恒定轴向拉拔力；

E1、E2——弹簧元件的刚度；

η1、η2——粘壶元件的粘滞系数。

理论上，一定的锚杆混凝土都对应着一特定流变力学模型，通过数学推导，可求出本构方程。但一般来说，要确切知道模型中的各元件的力学参数的具体数值是非常困难的。蠕变试验最能反映混凝土的流变性，其试验数据处理可以通过寻找回归方程与蠕变方程间的间接联系，通过这种联系，建立方程组，求解出蠕变方程中的流变力学参数。(www.chuimin.cn)

Burgers模型的蠕变方程式（6.57）可以写成：

式中

根据数学原理，指数函数exp（-Rt）可以用级数展开为：

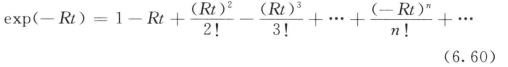
pagenumber_ebook=297,pagenumber_book=265

将上式代入式（6.59），整理后得：

比较式（6.58）得：

pagenumber_ebook=298,pagenumber_book=266

将根据锚杆蠕变试验解出的a0、a1、a2、a3代入式（6.62）求解：

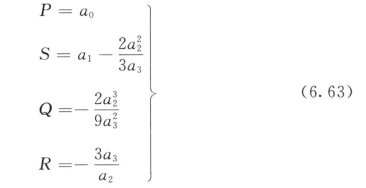
pagenumber_ebook=298,pagenumber_book=266

将式（6.63）代入式（6.59）得到Burgers模型的蠕变方程。由式（6.60）可以得到各元件的力学参数为：

pagenumber_ebook=298,pagenumber_book=266

然后，利用锚杆拉拔蠕变试验时间—位移曲线计算其力学参数。

2）加固效果。图6.20为试验锚杆拉拔蠕变试验时间位移曲线，经过对上述试验数据进行回归分析，求出了不同恒拉力下模型的力学参数。当锚杆拉拔力在68.4～397.3kN时，η1为相当大的数，η1=4.33×1015～3.36×1015（kN·min）/mm，从Burgers模型中η1的性质可知，相当于该元件不起作用，也就是说锚杆无蠕变变形发生；当锚杆拉拔力为430.0kN时，η1=3690.0（kN·min）/mm已经急剧减小，说明在该荷载作用下锚杆应力已经衰减。

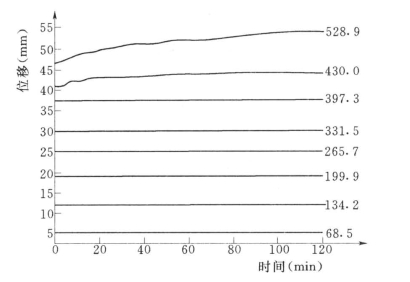
pagenumber_ebook=299,pagenumber_book=267

图6.20　锚杆拉拔蠕变试验时间位移曲线（单位：kN）

与此同时，继续对试验锚杆作长期观测，试验共持续观测了26个月，锚杆锁定时的拉力为423.6kN，至观测结束时锚杆拉力为375.5kN。图6.21为锚杆荷载随时间变化曲线。从试验曲线可以看出，锚杆拉力在锁定后的前4个月里衰减最快，4个月以后锚杆拉力基本趋于稳定，只在375kN上下微幅波动。因此，通过试验可知，锚杆长期工作的承载力约为375kN。

综合分析结果表明，宁车沽防潮闸基地质缺陷采用预应力土锚杆（索）加固，保证了该闸的正常运行。其长期加固抗拔力在375～430kN之间，平均在400kN左右是可靠的。

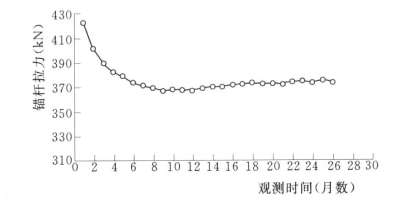
pagenumber_ebook=300,pagenumber_book=268

图6.21　锚杆荷载随时间变化曲线

水工程地质缺陷加固技术-预应力锚杆案例

相关推荐