我国学者邹金锋博士等基于损伤理论探讨了全长式锚杆荷载传递的作用机理[3]，为锚杆加固的设计、施工及管理提供了理论依据。当张拉荷载作用在锚杆上时，锚杆、岩土体共同承担着张拉荷载。图6.2锚固段荷载传递机理分析锚杆隔离体；锚杆单元考虑该锚杆单元体的轴向静力平衡条件，得式中τ——锚固段表面受到的剪应力。图6.5轴力沿锚杆长度分布的计算值与实测值对比结果表明，理论计算值与实测值基本相近，尤其是短锚杆更为一致。......
2023-11-04
全长锚杆灌浆锈胀机理及应用
【摘要】：在6.4.1节中介绍了全长式锚杆加固传递荷载的可靠性，本节阐述工程施工中和工程运行后因锈胀导致全长式锚杆失效的作用机理，以期在锚杆施工应用时合理地掌控其规律。影响全长粘结式灌浆锚杆锈胀力分析。表6.3全长粘结式灌浆锚杆锈胀力影响计算参数表图6.10锈胀力与钢筋锈蚀率之间的关系图6.11钻孔直径对锈胀力的影响图6.12灌浆材料强度对锈胀力的影响图6.13围岩体强度
在6.4.1节中介绍了全长式锚杆加固传递荷载的可靠性，本节阐述工程施工中和工程运行后因锈胀导致全长式锚杆失效的作用机理，以期在锚杆施工应用时合理地掌控其规律。
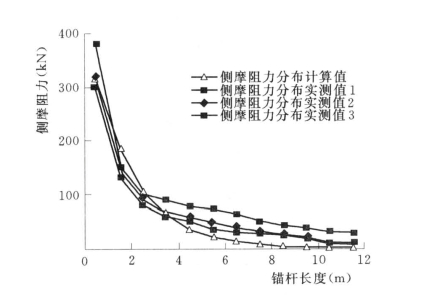
图6.6 侧摩阻力沿锚杆长度分布的计算值与实测值对比
我国学者何思明博士等以弹性理论为基础，并且根据锚杆、灌浆材料以及围岩体三者之间变形协调关系、荷载平衡条件，研究了锚杆锈胀导致灌浆或岩体开裂，进而加速锚杆锈蚀破坏的机制问题，讨论了锚杆锈胀量、灌浆材料特性、保护层厚度以及围岩体力学性质对锚杆锈胀力的影响。结果表明：锚杆锈胀力随着钢筋锈蚀率的增加而增加，随钢筋保护层厚度的增加而减小；砂浆与围岩体之间的锈胀力随砂浆强度、围岩强度的增加而增加，钢筋与砂浆之间的锈胀力随围岩强度的增加而增加，随砂浆强度的增加而降低[4]。
（1）灌浆锚杆体系的锈胀变形协调关系。边坡锚杆在某种因素作用下发生相变（生锈），导致体积膨胀，而钢筋受到灌注砂浆的约束，因此在钢筋与砂浆之间产生膨胀力；同样砂浆受到锈蚀钢筋施加的膨胀力后，与围岩体的接触面上也会产生径向变形，这种变形同样会受到围岩体的约束，进而在砂浆与围岩体之间也产生膨胀力。因此，钢筋、砂浆、围岩体这三者之间的相互作用关系是建立计算模型的理论基础。为此，首先建立这三者之间的变形协调关系（见图6.7）。
图6.7 灌浆锚杆体系钢筋锈蚀变形关系示意图
图6.7清楚地表述了全长式灌浆锚杆体系由钢筋（锚杆主体）、砂浆和围岩（锚固孔）三者组成并叠加的关系。
钢筋半径为R1、钻孔半径为R2。钢筋锈胀后，无约束自由变形量为δ、受外围灌浆材料的约束，实际变形量为δ1；砂浆体在膨胀力作用下的径向变形量设为δ2，根据钢筋、砂浆两者之间的变形协调关系，有如下关系式成立：
同样，假设砂浆在锈胀力作用力下，其外侧（与围岩体接触面上）产生的自由变形量为δ5，而实际上，砂浆会受到围岩体的约束，因此，在砂浆与围岩体接触面上会产生锈胀力。假设围岩体在锈胀力作用下产生的径向位移为δ4，而砂浆在内外锈胀力作用下在与围岩体接触面上产生的径向位移为δ3，则根据变形协调关系，有如下关系成立：
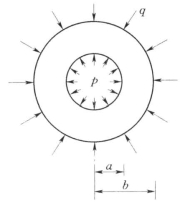
图6.8 轴对称问题基本解
（2）灌浆锚杆体系的锈胀力。
1）弹性力学厚壁圆筒的基本解。弹性力学轴对称问题的基本解如图6.8所示。
应力解：
位移解：
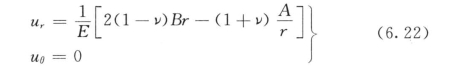
式中
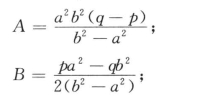
σr、σθ、τrθ——径向、环向和剪应力；
ν——材料的泊松比；
ur、uθ——径向和环向位移。
2）灌浆锚固在锈胀力作用下的计算模型。灌浆锚杆在锈胀力作用下，钢筋、砂浆、围岩体三者之间的锈胀力关系可用图6.9的模型来模拟。
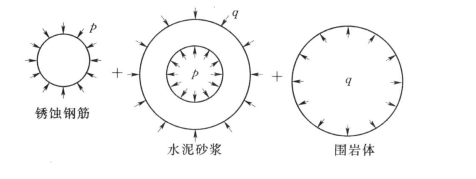
图6.9 灌浆锚杆体系钢筋锈胀力
①锈胀力作用下锈蚀钢筋变形计算。假设钢筋锈蚀后的净直径为dρ，名义直径为dm，则：
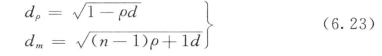
式中 n——钢筋锈蚀后体积膨胀率，通常为2～4；
ρ——钢筋锈蚀率，按照钢筋截面重量损失计算。
根据锈蚀钢筋的受力条件（见图6.9），可以求出锈蚀钢筋在锈胀力作用下与砂浆接触面上的径向位移：
式中
Eg、νg——铁锈的弹性模量和泊松比。
②锈胀力作用下砂浆变形计算。
a.砂浆在内外锈胀力共同作用下的变形计算。灌注砂浆的内外锈胀力作用下（见图6.9），根据弹性力学轴对称问题的基本解，并利用边界条件，可以计算出内外边界上的径向位移。
砂浆受力边界条件：
砂浆内外接触面上的径向位移为：
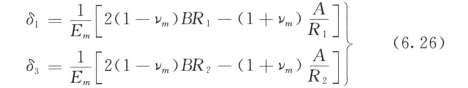
式中
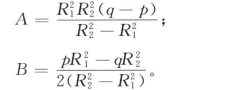
式（6.26）可以进一步简化为：
式中 δ1、δ2——砂浆内外接触面上的径向位移；
R1、R2——砂浆的内外半径；
Em、νm——砂浆的弹性模量和泊松比。
b.砂浆在仅有内侧锈胀力作用下的变形计算。砂浆在与钢筋接触面上的锈胀力作用下，其外侧（与围岩体接触面）自由变形的情况，利用轴对称问题的基本解和相应的边界条件可以计算出与围岩体接触面上的径向位移。(www.chuimin.cn)
砂浆受力边界条件：
砂浆内外接触面上的径向位移为：
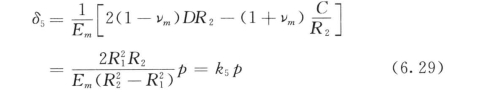
式中
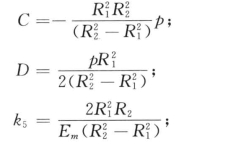
δ5——砂浆在内侧接触面上受到锈胀力作用，而外侧自由变形条件下的外侧接触面上的径向位移；
R1、R2——砂浆的内、外半径；
Em、vm——砂浆的弹性模量和泊松比。
③锈胀力作用下围岩体变形计算。围岩体在锈胀力q作用下，在与砂浆接触面上径向位移同样可以利用轴对称问题的基本解和相应的边界条件确定。
边界条件：
接触面上的径向位移为：
式中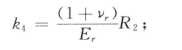
Er、νr——围岩体的弹性模量和泊松比。
④灌浆锚杆锈胀力计算。通过上面几节的分析，确定了锈蚀钢筋、砂浆以及围岩体在锈胀力作用下的变形计算公式，根据三者之间变形协调关系方程式（6.19）、方程式（6.20），就可以计算在给定钢筋锈蚀率的情况下，在钢筋与砂浆之间、砂浆与围岩体之间产生的锈胀力p和q。
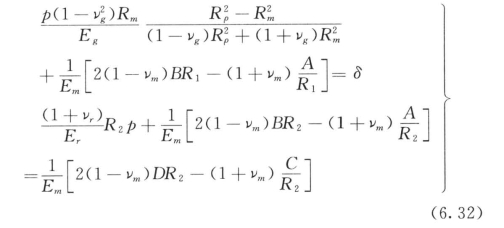
在方程式（6.32）中，仅有2个未知数p和q，因此，可以求解，直接计算给定钢筋锈蚀率情况下钢筋、砂浆、围岩体三者之间产生的锈胀力。
式（6.32）可以简化为：
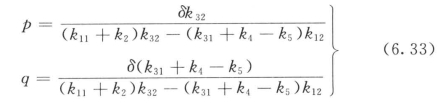
式中 符号意义同前。
（3）灌浆材料开裂特性及影响因素。
当钢筋锈蚀率达到一定程度后，在钢筋、砂浆、围岩体之间产生的锈胀力可能导致砂浆或围岩体开裂，使得砂浆或钢筋的保护层遭到破坏，影响锚杆体系的耐久性。在此，研究砂浆、围岩体锈胀致裂的条件。
1）锈胀力导致砂浆开裂的条件。根据轴对称问题的应力解，砂浆在内外锈胀力作用下，其环向应力可按下式计算：
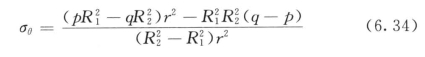
其最大环向应力出现在内边界上：
当砂浆内边界上的环向应力达到砂浆的抗拉强度时，就会导致砂浆开裂。于是给出砂浆锈胀致裂的条件：
式中 fsk——砂浆的抗拉强度。
2）锈胀力导致围岩体开裂的条件。类似于砂浆锈胀致裂分析，围岩体在锈胀力作用下，根据轴对称问题的应力解，其环向应力公式为：
其最大环向应力出现在内边界上：
当砂浆内边界上的环向应力达到围岩体的抗拉强度时，就会导致围岩开裂。于是可以给出围岩体锈胀致裂的条件：
式中 frk——围岩体的抗拉强度。
（4）影响全长粘结式灌浆锚杆锈胀力分析。为了验证（1）～（3）建立的锚杆锈胀模型的合理与可靠，何思明等给出了计算参数（见表6.3）和相应的计算结果（见图6.10～图6.13）。
表6.3 全长粘结式灌浆锚杆锈胀力影响计算参数表
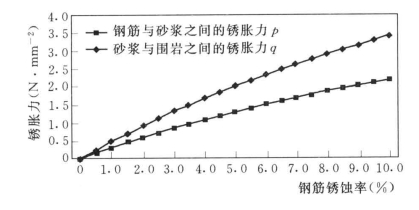
图6.10 锈胀力与钢筋锈蚀率之间的关系
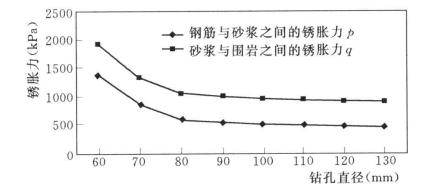
图6.11 钻孔直径对锈胀力的影响
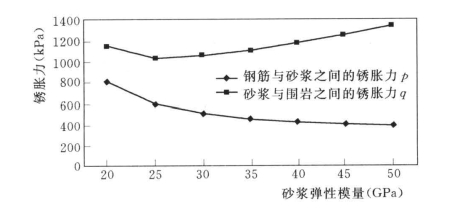
图6.12 灌浆材料强度对锈胀力的影响
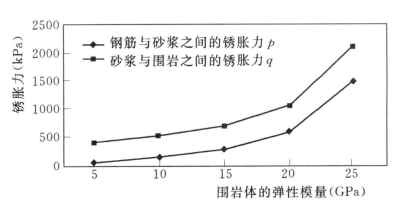
图6.13 围岩体强度对锈胀力的影响
从图6.10可以看出：随着钢筋锈蚀率的增加，作用在钢筋与砂浆之间以及砂浆与围岩体之间的锈胀力几乎成线性增加，因此，钢筋锈蚀越严重，锈胀力也越大，最终将导致砂浆或围岩开裂，进而加剧锚杆的锈蚀，降低锚杆的耐久性；锚杆锈胀力随钢筋保护层厚度（钻孔直径）的增加而减少（见图6.11），因此，可以通过增大锚杆的钻孔之间来减少锈胀力的作用；从图6.12可以看出：钢筋与砂浆之间的锈胀力随砂浆强度的增加而降低，而砂浆与围岩体之间的锈胀力却随砂浆强度的增加而增加；从图6.13中可以得出如下结论：无论是锚杆与砂浆之间的锈胀力还是砂浆与围岩之间的锈胀力均随围岩体强度的增加而增加，且具有相似的增长规律。
有关水工程地质缺陷常用加固技术的文章
- 详细阅读
-
岩石锚杆基础，《规范》方法及教程详细阅读
岩石锚杆基础适用于直接建在基岩上的柱基，以及承受拉力或水平力较大的建筑物基础。灌浆前，应将锚杆孔清理干净。 某岩石锚杆基础，锚杆孔直径采用80mm，孔深度为1200mm。锚杆筋体采用HRB335级钢筋，其直径为20mm，插入孔内长度为1150mm。......
2023-08-28
-
锚杆基础在输电线路中的应用及关键检测详细阅读
输电线路锚杆基础适用于基面以下是整块岩石的地质条件。采用锚杆基础施工时，首先使用钻孔机在岩石上钻孔，然后将地脚螺栓直接插入岩孔内，再用混凝土与岩石粘成一体。采用锚杆基础的输电线路铁塔遭遇强风袭击时，地脚螺栓会产生剪切力和上拔力。其中，锚杆上拔力试验是锚杆基础检测最为关键的部分。......
2023-06-29
-
小净距段对拉锚杆试验的工程应用成果详细阅读
1)测试项目及测试频率左线DK276+073和右线DyK276+073断面左右线同一根对拉锚杆上下各安装一个锚索测力计测量对拉锚杆的轴力。监测频率及时间根据监测数据和现场工程进展及时调整。图7.27围岩压力当前值断面分布图图7.28二次初衬开裂照片开裂后围岩压力开始减小。二次衬砌施作后压力变化减慢，均趋向稳定。通过记录隧道开挖过程中钢拱架的受力情况，对监测到的钢拱架应力做出初步分析，评价现......
2023-09-21
-
土层锚杆施工关键要点及验证方法详细阅读
对于土层锚杆，土变形和拉杆伸长占主要地位。如土层锚杆过于细长，则锚固体的伸长也不能忽视，而拉杆与锚固体砂浆间的徐变则是微小的。在土层锚杆施工前，应根据设计要求、土层条件和环境条件，合理选择施工设备、器具和工艺方法。做好砂浆的配合比及强度试验、土层锚杆焊接的强度试验，验证能否满足设计要求。......
2023-08-29
-
常用加固技术：新锚杆支护简述详细阅读
锚杆支护围岩强度强化理论。该理论揭示了锚杆的作用原理和加固围岩的实质，并为合理确定锚杆支护参数提供了合理的理论依据。它是中国矿业大学针对煤矿巷道的锚喷支护首次提出的。由于巷道周围形成了不利于围岩稳定的松动围岩，由此，松动圈的范围就决定了巷道的稳定性，也是锚杆支护设计的依据。......
2023-11-04
-
浙江长命排涝闸基加固案例：锚杆静压桩的成功应详细阅读
在运行过程中发现该排涝闸站闸室段底板下存在贯穿性的渗漏通道，闸室整体下沉约1cm，且闸底板西南侧存在严重的渗透破坏。图6.22长命排涝闸平面布置示意图由于长命排涝闸站闸室段基础原设计仅做开挖处理，土体发生破坏后不能有效承担上部荷载，因此必须对基础进行加固补强。表6.4闸室段不同工况应力情况表锚杆静压桩的设计与施工。......
2023-11-04
-
云南小湾水电站地下厂房岩锚梁锚杆加固案例详细阅读
图6.23小湾地下厂房岩台钻孔示意图表6.6小湾水电站地下厂房岩台钻孔及光爆装药参数表岩锚梁锚杆施工。②岩锚梁内设计受力锚杆，需要测量精确定位，控制施工偏差。岩锚梁受拉受压锚杆总数3258根。为确保岩锚梁开挖质量，共布置三排预应力锁口锚杆，要求在岩台爆破前施工完毕。图6.24小湾水电站地下厂房岩锚梁锚杆加固布置示意图3）锚杆孔的特殊处理。采用锚杆加固岩锚梁，安全稳定，运行正常。......
2023-11-04
相关推荐