首页理论教育土地冻融作用机制及加固技术

土地冻融作用机制及加固技术

2023-11-04 理论教育版权反馈

【摘要】：水工程的冻害问题主要由土体的冻胀、融沉作用造成。目前，我国对于土地冻融作用机制的研究，已由传统的冻土水分迁移与热质迁移转向力学机制出发，根据传热学、渗流理论及冻土力学的带相变的温度场、水分场和应力场的“三场耦合数值分析”[5]。

水工程的冻害问题主要由土体的冻胀、融沉作用造成。土体冻胀、融沉过程受控于土体中的水分场、应力场、温度场（统称三场）及其变化规律，本质是冻土多孔介质中土骨架、冰晶体、未冻水这三种物质在温度、土水势、压力与变形等外界因素作用下的相互运动、迁移、扩散与相变。

目前，我国对于土地冻融作用机制的研究，已由传统的冻土水分迁移与热质迁移转向力学机制出发，根据传热学、渗流理论及冻土力学的带相变的温度场、水分场和应力场的“三场耦合数值分析”^[5]。

（1）冻土的弹性模量研究。从细观力学的角度出发，考虑到冻土的物理力学机理及内部结构的复杂性，首先将冻土看作是完全由土和冰组成的复合体单元，而暂时不考虑水的影响，并忽略如孔隙率等因素的影响。令土和冰的弹性模量分别为Es、Ei，剪切模量为Gs、Gi，泊松比为νs、νi。下面各式中的下标s和i分别表示冻土中的土和冰的应力分量与应变分量。于是由细观力学的混合律理论可以得到冻土复合材料的等效弹性模量K和等效剪切模量G为：

式中　Ks、Gs、Ki、Gi——土和冰的体积模量和剪切模量。

根据各向同性材料的弹性常数之间的关系：K=E/3（1-2ν），G=E/2（1+ν）。

经推导后可以得到由土、冰的弹性模量和泊松比表示的冻土的等效弹性模量E和等效泊松比ν的表达式为：

式中　cs、ci——土和冰的体积含量（也称为体积分数），且满足关系式：cs+ci=1。

（2）冻土的损伤本构关系。根据Lemaitre等效应力原理，即应力σ作用在受损材料上引起的应变与等效应力σ作用在无损材料上引起的应变等价。受损冻土在一维状态下的应力—应变关系为：

式中　 pagenumber_ebook=190,pagenumber_book=158 ——损伤力学中的等效应力，此等效应力相当于土力学中的有效应力；

E——无损材料的弹性模量，即初始弹性模量，由式（4.43）确定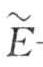； pagenumber_ebook=190,pagenumber_book=158 ——受损材料的弹性模量，即有效弹性模量；

D——损伤量。

因此，根据损伤力学理论，受损材料（D≠0）的本构关系可以从无损材料（D=0）的本构方程导出，只要用损伤后的有效应力来取代无损材料本构关系中的名义应力即所谓的Cauchy应力即可，由此得到冻土材料内部损伤型本构关系为：

（3）损伤演化规律。借助于混凝土损伤的一些研究结果，用双参数的Weibull分布表示冻土材料的损伤量D为：

式中　ε——应变；

n、a——形状参数和尺度参数，均为非负数。

经推导，可得：

上式即为以应变作为损伤演化控制量的损伤演化方程，εf为应力峰值所对应的应变值，n为表征材料损伤演化特征的材料参数。将式（4.48）代入式（4.46）中，从而得到冻土的损伤本构关系为：(www.chuimin.cn)

从上面的推导可以看出，冻土中任意点的应力σ与冻土的弹性模量、极限强度、应变峰值及该点的应变有关。冻土的损伤形状参数n是弹性模量E和割线模量Em的函数，一般可由实验或细观力学方法加以确定。

（4）三场耦合方程。我国学者朱志武等，基于上述本构关系并结合寒区路基土温度、水分、应力的“热、水、力”三场建立了“三场耦合方程”：

式中　Ce、 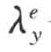pagenumber_ebook=191,pagenumber_book=159 、——路基土的等效容积热容量和x、y方向等效导热系数，其值分别为：

式中　λ、C——整个求解区域Ω内土体的导热系数和容积热容量；

ΔT——土体剧烈相变区温度区间长度的1/2。路基的静力平衡方程为：

几何方程为：

物理方程（本构方程）为：

上述本构方程中的弹性模量E和泊松比ν按式（4.43）和式（4.44）的计算结果来取值。

式（4.50）～式（4.58）即组成了描述冻土路基内含相变的温度场、水分场、应力场的三场耦合方程组。

【注释】

[1]李后强，艾南山.人地协同论——兼论人地系统的若干非线性动力学问题.地球科学进展，1996（2）

[2]冷崴，孙强.地震作用下结构失稳诱发的塌陷和地裂缝机理分析.灾害学，2007（1）

[3]雷伟.对我国城市地面沉降机理及社会效益的分析.工业技术经济，2006（3）

[4]郭雷，李夕兵，岩小明.岩爆研究进展及发展趋势.采矿技术，2006（1）

[5]朱志武，宁建国，马巍.土体冻融过程中水、热、力三场耦合本构问题及数值分析.工程力学，2007（5）