【摘要】:在这个问题中,告诉学生在某些有两个等量关系的实际问题中,列二元一次方程组比列一元一次方程更快捷,清楚。二元一次方程组概念的概括老师提请学生思考:上面的方程“x+y=88,x-y=10”中的x含义相同吗?根据上面的情境,得出有关方程的解的概念适合一个二元一次方程的一组未知数的值,叫作这个二元一次方程的解。
第一环节:情境引入
情境1
照片投影,并呈现问题:兰州市第五十六中学位于城关区,在2007年高考中,我校孟震煜同学取得684分的好成绩,在全省名列第十,兰州市名列第五,城关区名列第一,被复旦大学录取。此校是一所完全中学,初中与高中共有30个教学班,初中比高中多18个教学班,我校有多少个初中班,有多少个高中班?
请每个学习小组讨论(讨论2分钟,然后发言)。学生会用一元一次方程解决该问题,部分学生会用二元一次方程组解决。
这个问题由于涉及初中班级和高中班级的两个未知数,我们设:初中班级为x个,高中班级为y个,找到等量关系并列方程: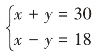
我校有教师88人,其中男教师比女教师多10人,请问我校有男女教师各多少人?(讨论2分钟,然后发言)。老师注意引导学生分析其中有几个未知量,如果分别设未知数,将得到什么样的关系式,能列出怎样的方程?
设:有x个男老师,有y个女老师
情境2
照片投影,并呈现问题:十一假期我们家8人去了红山公园,一共花了34元。红山公园成人票5元,学生票3元,他们家成人、学生各去了几人?
在这个问题中,告诉学生在某些有两个等量关系的实际问题中,列二元一次方程组比列一元一次方程更快捷,清楚。
设:成人有x人,学生有y人
第二环节:新课讲解,练习提高
(1)二元一次方程概念的概括
提请学生思考:上面所列方程有几个未知数?所含未知数的项的次数是多少?从而归纳出二元一次方程的概念:
含有两个未知数,并且所含未知数的项的次数都是1的方程。
教师对概念进行解析,要求学生注意,这个定义有两个要求:(www.chuimin.cn)
其一,含有两个未知数;
其二,所含未知数的项的次数都一次。
再呈现一些关于二元一次方程概念的辨析题,进行巩固练习。
(2)二元一次方程组概念的概括
老师提请学生思考:上面的方程“x+y=88,x-y=10”中的x含义相同吗?y呢?由于x、y的含义分别相同,因而必须同时满足“x+y=88,x-y=10”。我们把这两个方程用大括号联立起来,写成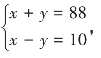 从而得出二元一次方程组的概念,即像这样共含有两个未知数的两个一次方程所组成的一组方程。如:
从而得出二元一次方程组的概念,即像这样共含有两个未知数的两个一次方程所组成的一组方程。如:
注意:在方程组中,各方程中的同一个字母必须表示同一个对象。
再呈现一些辨析题,让学生进行巩固练习。
(3)根据上面的情境,得出有关方程的解的概念
适合一个二元一次方程的一组未知数的值,叫作这个二元一次方程的解。
二元一次方程组中各个方程的公共解,叫做二元一次方程组的解。
然后,同样呈现一些辨析性练习。(投影)
第三环节:课堂小结
以结构表的形式梳理本堂评价所学:
问题情境:鸡兔同笼
第四环节:布置作业(略)

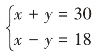
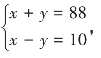 从而得出二元一次方程组的概念,即像这样共含有两个未知数的两个一次方程所组成的一组方程。如:
从而得出二元一次方程组的概念,即像这样共含有两个未知数的两个一次方程所组成的一组方程。如:







相关推荐