【摘要】:表4.9掺加SBC后体系中离子强度以及双电层厚度计算从表4.9可见,随着减水剂浓度提高,体系中离子强度增加,导致双电层被进一步压缩,这与测定的水泥颗粒ζ电位值随减水剂的加入而提高的结果一致。表4.12空间位阻作用力图4.34空白试样中水泥颗粒间作用力掺加SBC后水泥颗粒总受力无吸附层时水泥颗粒间作用力情况如图4.34所示。图4.35不考虑空间位阻作用的水泥颗粒间作用力图4.35是掺加SBC后不考虑空间位阻作用的水泥颗粒间作用力。
将不同浓度的SBC掺加到水泥净浆中,测定ζ电位以及吸附层厚度,其结果已经在第4章中进行讨论,空白试样、1%掺量SBC8、1%SNF的ζ电位分别为+8.9mV、-31mV和-32mV,掺加SBC8的水泥吸附层厚度3.72nm,掺加SNF的吸附层厚度仅为0.83nm,SMHE的吸附层厚度为6.82nm。这些数值将用来计算分散体系中水泥颗粒的受力情况。
(1)颗粒间静电斥力作用。Flatt通过等价二元电解质模型描述了包含有多种不同电解质的水泥悬浮液,评价了三参数Debye—Hückel近似方法对于球形粒子间静电斥力的有效性,其有效范围在水泥悬浮体的离子强度范围之内,因此静电斥力可用如下式表示:
式中:ε为水的相对介电常数,25℃时,取值78.38;ε0为真空电容率,8.85×10-12F/m;ε·ε0=6.94×10-10F/m;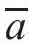 =2r1r2/(r1+r2),调和平均半径;Ψ为动电电位;κ为Debye-Hückel常数,其倒数为双电层厚度;h为颗粒间的距离;e为电子电荷,1.602×10-19C。
=2r1r2/(r1+r2),调和平均半径;Ψ为动电电位;κ为Debye-Hückel常数,其倒数为双电层厚度;h为颗粒间的距离;e为电子电荷,1.602×10-19C。
根据Neubauer等的研究,水泥浆体溶液中的离子强度可按下式计算:
体系中除OH-以外,其他离子浓度均可以采用ICP方法测得,所以根据水泥浆中离子浓度之间的关系可以计算得到COH-。
κ取决于溶液的离子浓度,可按下式计算:
式中:F为Faraday常数,其值为9.648×104C/mol;T为绝对温度。
当加入不同种类外加剂时,由于各种外加剂化学组成、取代基种类、取代度和离子种类等均不相同,引入水泥浆中的离子浓度存在差异。对于SBC8(DS=0.67)而言,电离时主要产生Na+、—SO32-两种基团,假如引入的减水剂大分子完全电离,则掺加水泥质量0.5%的SBC8相当于浓度(以AGU+0.67c[SO32-]计)为102.13mmol/L,1%SBC相当于204.26mmol/L。在w/c为0.45的条件下,采用上述ICP检测结果计算SBC不同掺量时的双电层厚度如表4.9所示。
表4.9 掺加SBC后体系中离子强度以及双电层厚度计算
从表4.9可见,随着减水剂浓度提高,体系中离子强度增加,导致双电层被进一步压缩,这与测定的水泥颗粒ζ电位值随减水剂的加入而提高的结果一致。
计算这种静电斥力的关键问题是水泥颗粒表面势能Ψ的测定,由于Ψ是Stern层外界的势能,通常使用实验测定的ζ电位值替代,而ζ电位是比Stern层稍远的一个剪切面上的电势,这样会导致静电斥力的估算值偏低,但多数情况下这一近似值是适用的。水泥颗粒表面势能Ψ与测定的ζ电位之间的关系可见图4.32。
图4.32 水泥颗粒吸附有机外加剂后双电层及电位变化示意图
当水泥颗粒表面有厚度为δ的吸附层时,静电作用力公式可以改写成式(4.10)形式。
假设两个水泥颗粒半径分别为10μm和30μm,可以通过式(4.9)和式(4.10)计算两者之间吸附减水剂SBC8前后的静电斥力,结果如表4.10所示。
表4.10 静电斥力的计算(r1=10µm,r2=30µm,a=1.33×10-5m)
(2)范德瓦耳斯引力作用。对于水泥悬浮液的尺寸范围,Flatt采用下式表达范德瓦耳斯吸引力:
式中:h为颗粒间距;A为Hamaker常数。
当颗粒间距h<<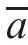 时,上式可简化为:
时,上式可简化为:
Sakai等采用水泥组分的Hamaker常数A为4.55×10-20J,Yang在计算水泥粒子间范德瓦耳斯作用力时A取2.33×10-20J。当水泥颗粒吸附有机高分子,覆盖有机高分子的水泥颗粒的Hamaker常数应该会变小,水泥颗粒之间的范德瓦耳斯引力减小。(https://www.chuimin.cn)
对半径分别为10μm和30μm的水泥颗粒,在水中受到的范德瓦耳斯引力可采用式(4.12)计算。考虑吸附层厚度对范德瓦耳斯引力影响时,可将式中h用(h+2δ)代替进行计算。计算结果见表4.11和图4.33。可见,吸附层的存在会降低颗粒间范德瓦耳斯引力。
表4.11 掺加SBC8的范德瓦耳斯引力
(吸附层厚度为3.72nm,A取4.55×10-20J,a=1.33×10-5m)
图4.33 有无吸附层的水泥颗粒间范德瓦耳斯引力
(3)空间位阻作用
水泥颗粒吸附减水剂以后,在水泥颗粒表面形成一定厚度的吸附层,当吸附层相互接触开始重叠时,吸附层之间相互压缩,产生位阻作用,压缩程度越大,这种位阻作用力变得越明显,位阻作用的这种增长取决于聚合物的吸附方式(构象)。Pedersen及Bergstrom认为,以蘑菇状的形态被吸附的聚丙烯酸,可以采用De Gennes的标度理论来计算位阻作用力,如式(4.13)所示。
式中:s为两个相邻聚合物粒子质心之间的距离,其值可由吸附实验测定的吸附层厚度代替;L为伸入溶剂中的最大长度。对SBC而言,其分子结构上存在—CH2CH2CH2CH2SO3Na基团,并且分布不均匀,吸附在水泥颗粒表面,形成不同的形态,分子链在水泥颗粒上可形成环状结构,L值采用测定的吸附层厚度。因此对于SBC,可设s=L=3.72nm,以计算空间位阻作用力。
设两个水泥粒子半径分别为10μm和30μm的,其调和平均半径为13.3×10-6m,温度为293K时,kBT值为4.12×10-21J,水泥颗粒吸附减水剂后表面形成一定厚度的吸附层,在不同颗粒间距的颗粒间空间位阻作用力见表4.12。由表4.12可见,随着颗粒间距的减小,颗粒表面的吸附层相互压缩程度的提高,颗粒间产生的位阻作用越强烈。
表4.12 空间位阻作用力
图4.34 空白试样中水泥颗粒间作用力
(4)掺加SBC后水泥颗粒总受力
无吸附层时水泥颗粒间作用力情况如图4.34所示。水泥颗粒在该条件下,不考虑重力的影响,由于没有吸附层存在,主要受静电斥力和范德瓦耳斯引力作用,前者较小,所以总的作用力为负值,即说明在水中分散的水泥颗粒之间是以范德瓦耳斯引力为主,颗粒间会发生自动聚集。
图4.35 不考虑空间位阻作用的水泥颗粒间作用力(掺加SBC)
图4.35是掺加SBC后不考虑空间位阻作用的水泥颗粒间作用力。从图4.35可知,当不考虑空间位阻作用时,可认为水泥分散体系中颗粒间作用依然是范德瓦耳斯引力和静电斥力,但是由于水泥颗粒吸附了SBC产生一定厚度的吸附层,削弱了范德瓦耳斯引力作用,在颗粒间距为1~10nm范围内,体系中作用力以静电斥力为主导;当颗粒间距超过10nm,则是范德瓦耳斯引力占据主要地位。说明水泥颗粒吸附SBC后,水泥颗粒的分散主要依赖于静电斥力作用。
图4.36是考虑空间位阻作用时,水泥颗粒间相互作用情况。当水泥颗粒相互靠近到吸附层能够接触时(2倍的吸附层厚度,即7.44nm),吸附层开始相互压缩,此时产生的作用力远远大于水泥颗粒间的静电斥力,越靠近相互作用越强烈,此时可以认为空间位阻作用力占主导地位。
通过以上分析可知,水泥颗粒表面吸附SBC形成3.72nm的吸附层,减弱了颗粒间范德瓦耳斯引力作用,在水泥颗粒间距为0~7.44nm时,主要是空间位阻作用起对水泥颗粒的分散作用,而在7.44~10nm范围时,是静电斥力发挥主要分散作用,超出10nm则是以范德瓦耳斯引力作用为主,颗粒会相互聚集。
图4.36 掺加SBC的水泥颗粒受力

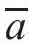 =2r
=2r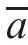 时,上式可简化为:
时,上式可简化为:





相关推荐