回归分析的基本思想和方法以及“回归”名词的由来，要归功于英国统计学家高尔顿（Galton）．高尔顿和他的学生、现代统计学的奠基者之一皮尔逊（Pearson）在研究父母身高与其子女身高的遗传关系时，观察了1 078对夫妇，以每对夫妇的平均身高作为x，而取他们的一个成年儿子的身高作为y，将这些数据画成散点图，发现趋势近似一条直线＝33．73＋0．516x（单位：英寸，1英寸＝2．54 cm）．这表明：......
2023-11-18
大学物理实验：最小二乘法的线性回归
【摘要】：在一元线性回归中，确定常数A和B，相当于在作图法中求直线的截距和斜率。图0-4密集分布 图0-5分散分布 方程的线性回归，用手工计算是很麻烦的。但是，不少袖珍型函数计算器上均有线性回归的计算键，计算起来极为方便，因此，线性回归的应用日益普及。
将实验结果画成图线可以形象地表示出物理规律，但图线的表示往往不如用函数表示那样明确和定量化。另外，用图解法处理数据，由于绘制图线有一定的主观随意性，同一组数据用图解法可能得出不同的结果。因此，下面将介绍一种利用最小二乘法来确定一条最佳直线的方法，从而准确地求出两个测量值之间的线性函数关系 （即经验方程）。由实验数据求经验方程，叫做方程的回归。
回归法首先要确定函数的形式。函数形式的确定一般是根据理论的推断或者从实验数据变化的趋势而推测出来。如果推断物理量y和x 之间的关系是线性关系，则可把函数写成如下形式
自变量只有x一个，故称为一元线性回归。这是方程回归中最简单、最基本的问题。
回归法可以认为是用实验数据来确定方程中的待定常数。在一元线性回归中，确定常数A和B，相当于在作图法中求直线的截距和斜率。
以下讨论最简单的情况，即每个测量值都是等精度，且假定x和y值中只有y有明显的测量随机误差。如果x和y均有误差，只要把相对来说误差较小的变量作为x即可。
若实验得到的数据是
相对应的有
方程（0-1）既然是物理量y和x间所服从的规律，则在A、B确定以后，如果实验没有误差，把 （x1，y1）、（x2，y2）、…、 （xm，ym）代入方程 （0-1）时，方程的左右两边应该相等。但实际上，测量总伴随着测量误差，我们把这些测量归结为y的测量偏差，并记作ε1、ε2、…、εm。这样，把实验数据（x1，y1）、（x2，y2）、…、（xm，ym）代入方程（0-1）后，得到
图0-3 直线y=A+Bx
把式（0-3）分别对A和B 求偏微分，得
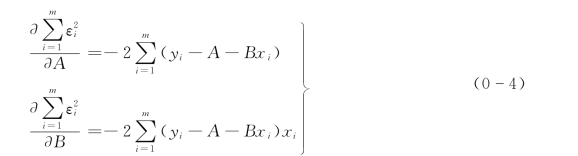(www.chuimin.cn)
令式（0-4）等于零，得
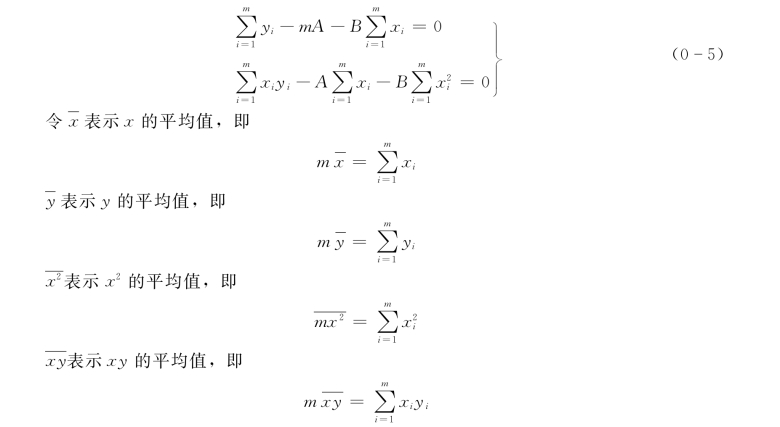
代入式（0-5），得
解方程，得
式中 A——直线y=A+Bx的截距；
B——斜率。
用回归法处理数据最困难的问题在于函数形式的选取。函数形式的选取主要靠理论上的分析，在理论还不清楚的场合，只能靠实验数据的趋势来推测。这样，对于同一组实验数据，不同的人员可能取不同的函数形式，得出不同的结果。为了判断所得的结果是否合理，在待定常数确定以后，还需要计算一下相关系数r。对于一元线性回归，r定义为
可以证明，r的值总是在0～1之间。r值越接近1，说明实验数据点密集地分布在所求得的直线的近旁，用线性函数进行回归是合适的，如图0-4所示。相反，如果r值远小于1而接近于0，如图0-5所示，说明根据实验数据求得的直线很分散，即用线性回归不妥，必须用其他函数重新试探。
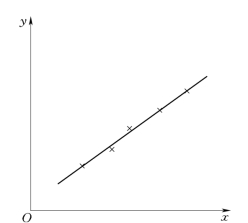
图0-4 密集分布 （r值接近于1）
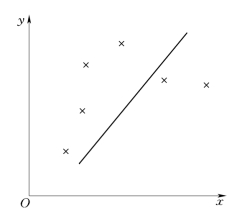
图0-5 分散分布 （r值接近于零）
方程的线性回归，用手工计算是很麻烦的。但是，不少袖珍型函数计算器上均有线性回归的计算键（具体用法详见所用计算器的使用说明书），计算起来极为方便，因此，线性回归的应用日益普及。
有关大学物理实验的文章
- 详细阅读
-
基础多元线性回归统计分析详细阅读
多元线性回归的数学模型可以用矩阵形式表示为1.参数β的最小二乘估计设b0，b1，…表4-1 回归正交设计计算表通过推导，可以得到方差分析表4-2。表4-2 方差分析表3.回归方程的显著性检验F＞Fα 若式成立，我们可以认为在显著水平α下，线性回归方程（4-6）是有显著意义的。反之，则认为线性回归方程没有什么意义，这时需要查明原因，具体情况具体分析。......
2023-06-27
-
密立根油滴实验：大学物理实验成果详细阅读
密立根是著名的实验物理学家，他从1907年开始着手电子电荷量的测量研究，到1911年宣布实验的结果。密立根的实验设备简单而有效，构思和方法巧妙而简洁。OM98BCCD微机密立根油滴仪。用K2 将油滴移至某条刻度线上，仔细调节平衡电压，这样反复操作几次，经一段时间观察油滴确实不再移动才认为是平衡了。......
2023-11-02
-
大学物理实验：光的等厚干涉的实验成果详细阅读
牛顿环是等厚干涉的一个最典型的例子，最早为牛顿所发现，但由于他主张的微粒学说而未能对它作出正确的解释。观察光的等厚干涉现象，了解等厚干涉的特点。这一现象是牛顿发现的，故称这些环纹为牛顿环。......
2023-11-02
-
使用一元线性回归进行推测详细阅读
回归方程最有效的用途就是在给定自变量数值x=x0的前提下，推算因变量的数值y=y0。点估计方法是指将自变量数值x=x0代入回归方程，用计算的回归估计值=直接作为因变量y0的估计值。值得注意的是，回归方程只能以自变量x推算因变量y，而不能反过来以因变量y推算自变量x。......
2023-08-13
-
生态数据分析：多元线性回归详细阅读
式（7-1）就是多元线性回归的数字模型。（二）建立多元线性回归方程设y对x1，x2，…，m）称为高斯乘数，是多元线性回归分析假设检验与进一步统计分析所需要的。建立产量y与穗数x1、每穗粒数x2的二元线性回归方程。如果此回归关系是真实的，则可依据该二元线性回归方程由穗数x1、每穗粒数x2预测和控制产量y。统计学已证明，在m元线性回归分析中，离回归平方和的自由度为。......
2023-11-17
-
生态数据分析：多元线性回归的假设检验详细阅读
，βm不全为零在H0成立条件下，有由上述统计数F进行F检验即可推断多元线性回归关系的显著性。［例6］对［例5］所建立的二元线性回归方程进行假设检验。表7-2二元线性回归方差分析表二、偏回归系数的假设检验上述多元线性回归关系假设检验是检验各自变量共同对因变量的线性影响是否显著。因此，当多元线性回归关系显著时，还必须逐一对各个偏回归系数进行假设检验，发现并剔除对因变量的线性影响不显著的自变量。......
2023-11-17
-
大学物理实验：有效数字的运算技巧详细阅读
按照保留一位可疑数字的原则，计算结果应写成1.23，为三位有效数字。根据以上的截尾原则，将下列数截去尾数成四位有效数字时，应有2.34526 →2.3452.34550 →2.3462.34650 →2.3462.34750 →2.3486.数字的科学记数法在乘除和开方等运算中，对数字采用科学记数常常是比较方便的。......
2023-11-02
相关推荐