【摘要】:时域有限差分方法适合宽频带电磁问题分析,如宽带天线和电磁屏蔽效能、雷击等应用。1966年,K.S.Yee首次提出一种电磁场数值计算新方法—时域有限差分方法。FDTD方法用于求解微分形式的麦克斯韦旋度方程组,利用差分原理将旋度方程组离散成为一组时域递推公式。
时域有限差分方法适合宽频带电磁问题分析,如宽带天线和电磁屏蔽效能、雷击等应用。
1966年,K.S.Yee首次提出一种电磁场数值计算新方法—时域有限差分(Finite Difference Time Domain,FDTD)方法。FDTD方法用于求解微分形式的麦克斯韦旋度方程组,利用差分原理将旋度方程组离散成为一组时域递推公式。它是一种时域直接解法,随着时间的推进可以很方便地知道电磁场随时间的变化过程,在电磁工程各方面都得到了广泛应用。
麦克斯韦方程组的微分旋度方程为

式中,E为电场强度,单位为伏特每米(V/m);H为磁场强度,单位为安培每米(A/m);D为电通量密度,单位为库仑每平方米(C/m2);B为磁通量密度,单位是韦伯每平方米(Wb/m2);J为电流密度,单位是安培每平方米(A/m2);Jm为磁流密度,单位是伏特每平方米(V/m2)。
各向同性线性媒质中的本构关系为

式中,ε表示介质介电参数,单位为法拉每米(F/m);µ表示磁导系数,单位为亨利每米(H/m);σ表示电导率,单位为西门子每米(S/m);σm表示磁导率,单位为欧姆每米(Ω/m)。
在直角坐标系中,式(2-43)和式(2-44)可写为下式
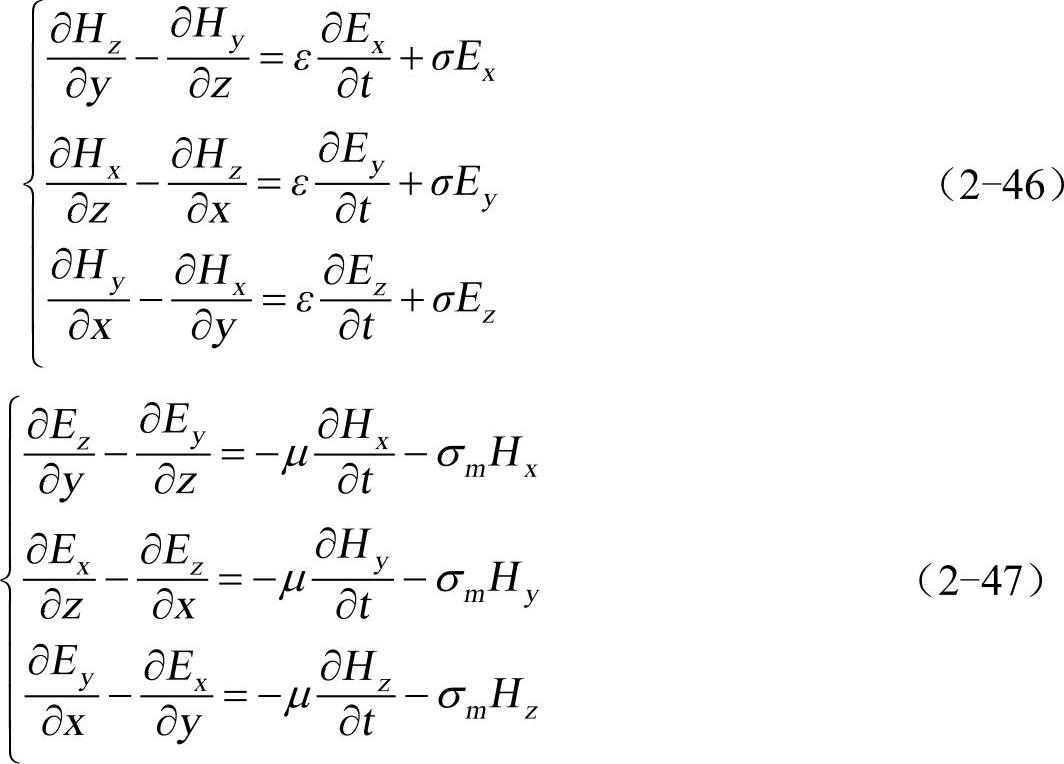
Yee元胞中电场与磁场各结点的位置关系如图2-12所示,每个磁场分量由4个电场分量围绕,同样每个电场分量由4个磁场分量围绕,这种电磁场分量的空间取样方式适用于麦克斯韦方程的差分计算,也能够很好地描述电磁场的传播特性,电场与磁场在时间顺序上交替采样,抽样的时间间隔相差半个时间步,这样麦克斯韦方程组离散后变为显示差分方程,可以直接迭代求解,不需要求解矩阵。只需要给出初始值和边界条件就可以逐步迭代求出各个时间步的空间电磁场分布。
 (www.chuimin.cn)
(www.chuimin.cn)
图2-12 FDTD离散中的Yee元胞
数值稳定条件:FDTD算法中数值解的稳定性主要与时间步长∆t和空间离散尺度∆x、∆y、∆z有关,为了保证数值稳定性,它们必须满足一定关系,可以推导出各离散参数应该满足如下关系式
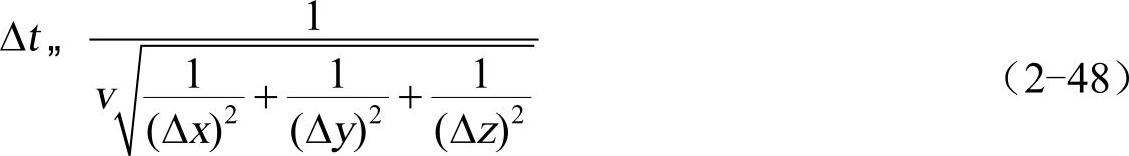
这就是FDTD的数值稳定条件,又称为Courant稳定条件。其中,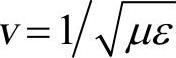 为介质中的光速,如果媒质不均匀,那么不同区域电磁波的速度v不同,那么应该取速度最大值。普通FDTD通常采用均匀网格,3个方向的网格离散相同,即∆x=∆y=∆z=∆s,Courant稳定条件变为下式
为介质中的光速,如果媒质不均匀,那么不同区域电磁波的速度v不同,那么应该取速度最大值。普通FDTD通常采用均匀网格,3个方向的网格离散相同,即∆x=∆y=∆z=∆s,Courant稳定条件变为下式

数值色散:平面波在自由空间中传播时,其相速度与频率无关,由于FDTD方法采用了差分近似后导致相速度与频率有关,称之为数值色散,这种色散也与空间离散间隔有关,只有离散间隔足够小的时候,这种数值色散的影响才可以忽略。
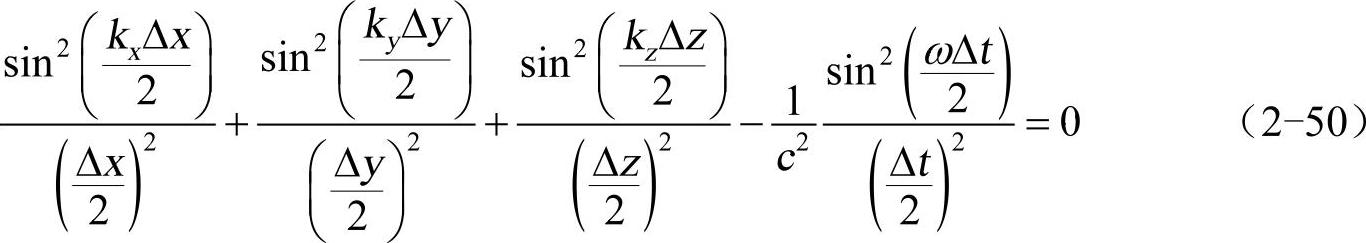
式(2-50)为FDTD方法中数值色散的一般表达式,表明FDTD计算中波的传播速度与传播方向有关,这是离散后引起的各向异性特性,当∆x、∆y、∆z、∆t趋于零的时候式(2-50)变为式(2-51)。

式(2-51)为自由空间平面波的关系,此时色散的影响可以减小到任意小,但是这样必然会导致计算时间和内存的增加。所以要选择合适的网格剖分尺寸。实际计算中一般要求:




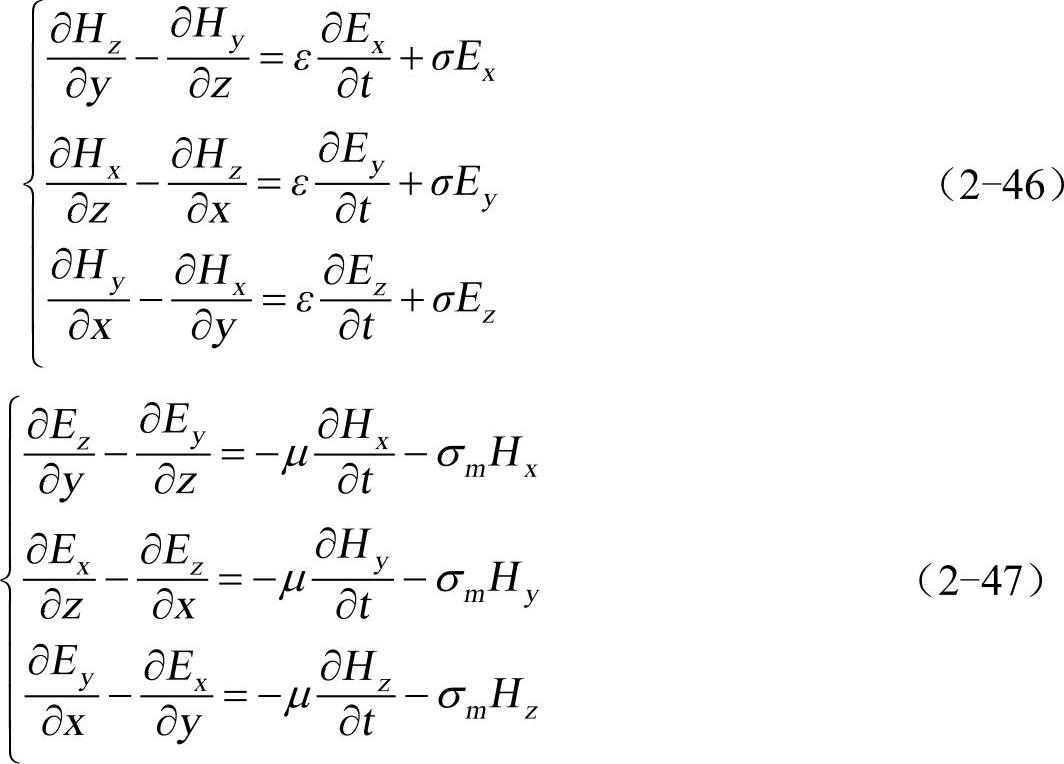
 (www.chuimin.cn)
(www.chuimin.cn)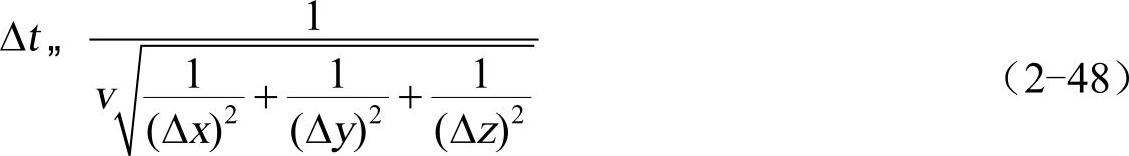
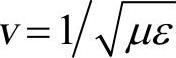 为介质中的
为介质中的
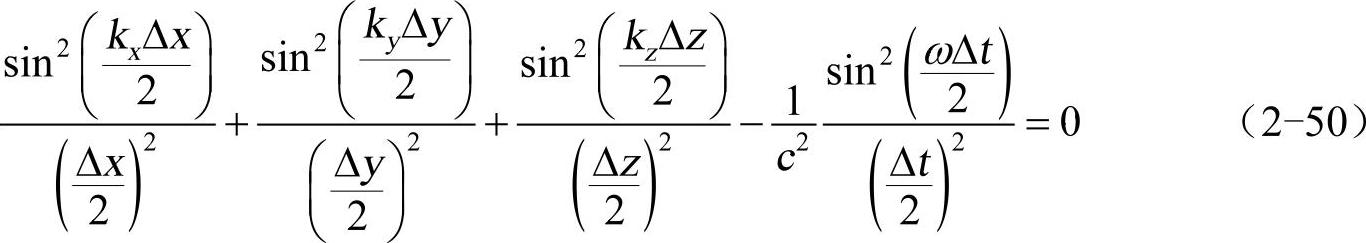








相关推荐