FEKO仿真原理的实现和应用

2023-10-31 理论教育版权反馈

【摘要】：用矩量法求解该算子方程的步骤如下：1）选择一组带有未知数的基函数{ji}iN=1表示未知等效流或场，即。用矩量法求解电磁场问题的优点是严格地计算各子散射体间的互耦，矩量法本身保证了计算误差的系统总体最小而不会产生数值色散问题。具体表达为传统阻抗元素计算方法是对应于每一个基函数和权函数而言的。

1.矩量法的基本原理

矩量法是指将算子方程化为矩阵方程，然后求解该矩阵方程的方法。例如，描述物理系统的算子方程为

L(x)=b （2-1）

式中，x为未知等效流或场；b为已知激励源。用矩量法求解该算子方程的步骤如下：

1）选择一组带有未知数的基函数{j_i}_i^N₌₁表示未知等效流或场，即。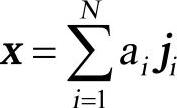

2）选择加权函数或检验函数t_j，并对算子方程两边求内积得

式（2-1）进一步写为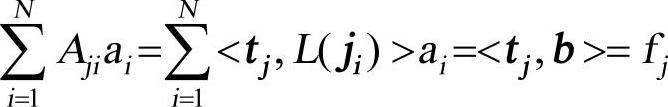，或写为矩阵形式[A][a]=[f]。

3）用直接法或迭代法求解这一矩阵方程[A][a]=[f]，从而获得等效流或场的未知数向量[a]。

4）由求得的等效流代入积分方程求解任意点的场。

用矩量法求解电磁场问题的优点是严格地计算各子散射体间的互耦，矩量法本身保证了计算误差的系统总体最小而不会产生数值色散问题。因为由矩量法离散获得的矩阵一般为满阵，所以阻抗矩阵的存储量为O(N²)，直接求解和迭代求解矩阵方程的计算复杂度为O(N³)和O(N²)，当问题的电尺寸变得很大时，其存储量和计算量将会很大。随着计算机性能的飞速提高和计算数学的发展，以矩量法为基础的一些高效方法，如多层快速多极子方法（MLFMM），在保证精度的同时极大地减少了计算时间和内存需求，因此矩量法及其快速算法已经在工程中得到了广泛应用。

2.RWG基函数，伽略金方法

RWG基函数是Rao，Wilton，Glisson于1982年提出的定义在相邻平面三角贴片上的基函数，又称为广义屋脊基函数，其简单示意图如图2-1所示。通常，选择权函数与基函数形式一样，即采用伽略金方法。这种基、权函数能较好地模拟散射体表面感应电流分布，不会造成人为电荷的堆积，保证了电流的连续性。由于平面三角贴片能灵活模拟任意复杂的三维几何形体，如尖点、凹槽及目标表面的凸起物，因此平面三角贴片和RWG基函数在复杂形体目标的电磁散射分析中广泛应用。

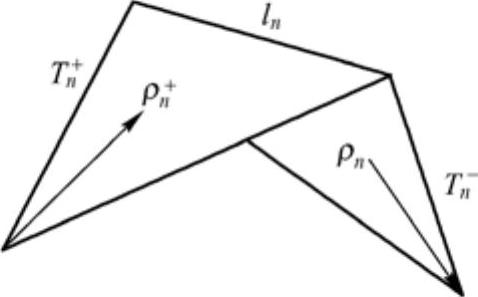
图2-1 平面三角贴片和RWG基函数

RWG基函数的定义式为

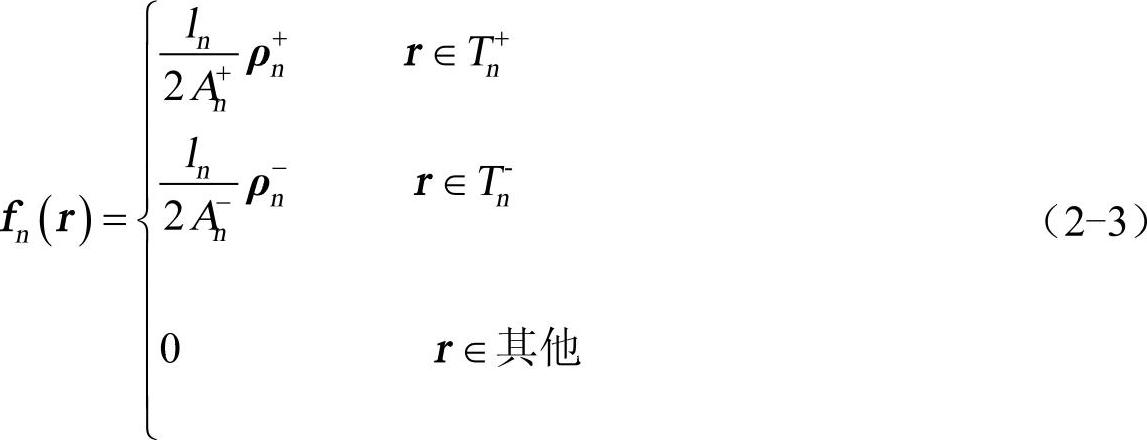
式中，T_n⁺、T_n⁻为第n个基函数所对应的两个相邻三角形；ln为公共边长度；A_n⁺、A_n⁻分别为三角形T_n⁺、T_n⁻的面积；ρ_n⁺、ρ_n⁻分别为三角形Tn+的顶点指向该三角形的场点和三角形T_n⁻上的场点指向该三角形顶点的矢量。由式（2-3）可得到基函数f_n(r)的散度。可以看出，在T⁺_nT⁻_n、上电荷密度均匀，两相邻三角形的总电荷为零，没有线电荷的堆积，这样保证了相邻三角形单元两边电流的连续性。

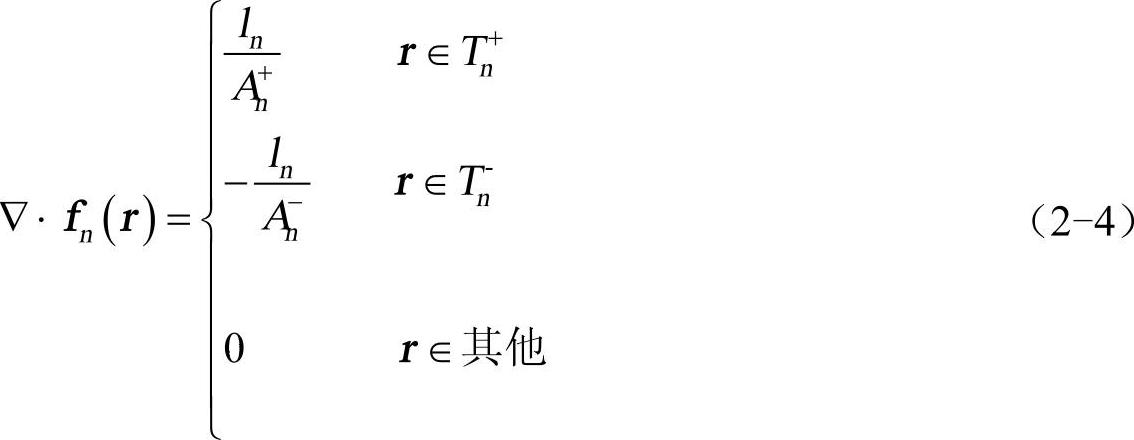
考虑由标量位和矢量位构成的导体的电场积分方程，采用平面三角形贴片、RWG基函数、伽略金方法的阻抗元素计算。

−E_tⁱ_an(r)=(iwA(r)−∇φ(r))_tan,r在导体边界面上（2-5）

对于伽略金方法，权函数与基函数相同，在式（2-5）两边取权函数f_m作内积，得到

＜Eⁱ,f_m＞=−iw＜A,f_m＞+＜∇φ,f_m＞（2-6）

利用矢量运算公式与φ在三角形上面积分的几何重心近似，最终可得到

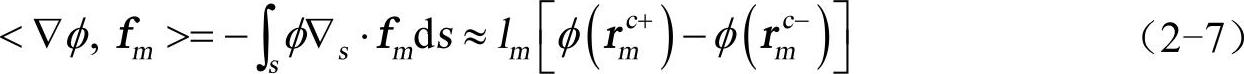
式中，r_m^c+、r_m^c−分别为权函数f_m所对应的三角形T_m⁺、T_m⁻几何重心的场矢量。

同理，利用几何重心近似，可得

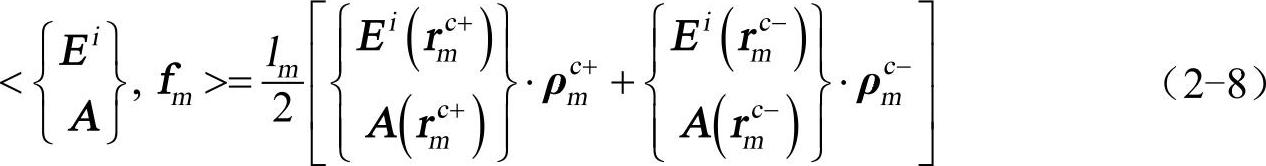
式中，ρ_m^c+为三角形顶点流出到点r_m^c+的矢量；ρ_m^c−为从点r_m^c−流入到三角形顶点的矢量。将导体表面感应电流用基函数展开，式（2-6）则可写成如下矩阵方程的形式

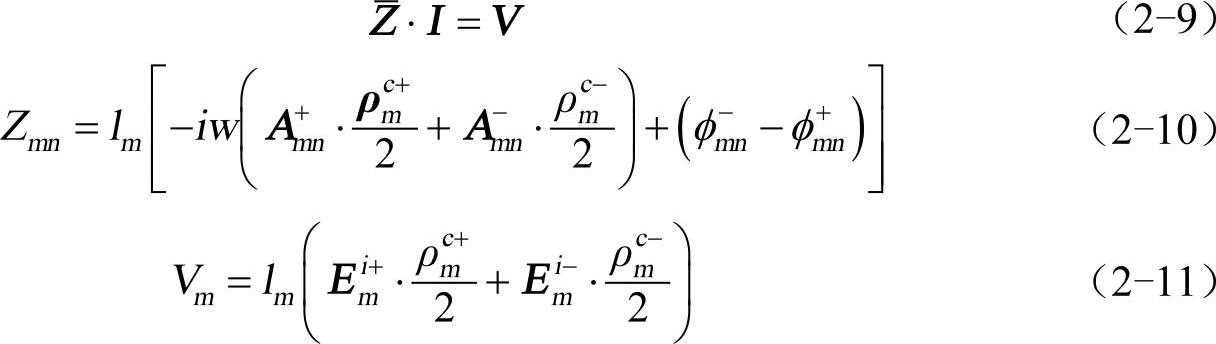
式中，I为待求电流矢量；A_m^±_n为基函数f_n在权函数对应的三角形重心r_m^c±处产生的矢量位；φ_m^±_n为基函数^f_n在权函数对应的三角形重心r_m^c±处产生的标量位。具体表达为(www.chuimin.cn)

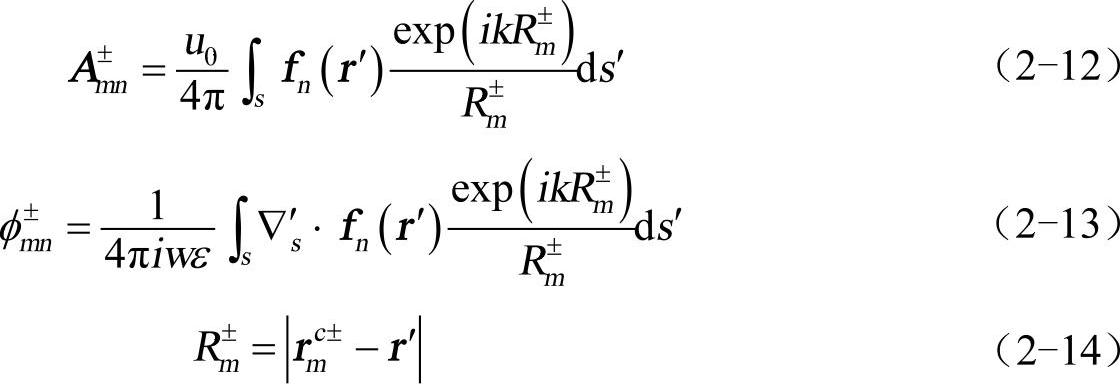
传统阻抗元素计算方法是对应于每一个基函数和权函数而言的。对于RWG基函数每个三角形（边缘三角形除外）均对应于3个基函数和3个权函数。这意味着采用传统阻抗元素计算方法时，对给定的一个场三角形和一个源三角形，共有9个阻抗元素与之对应，所以在该源三角形上的面积分要计算9次。当三角形贴片数量很多时，阻抗元素的计算效率将很低。为高效计算阻抗元素，可以采用平面三角对组合计算（face-pair combination）来代替传统的阻抗元素计算方法。平面三角对组合计算针对给定的一个场三角形、一个源三角形开展。对给定的场三角形、源三角形，在源三角形上的面积分只计算3次，因此大大提高了阻抗元素的计算效率。图2-2所示表示出了在全局坐标系中任意的一个场点三角形Tp与源点三角形Tq的几何关系。其中，r₁、r₂、r₃分别为源三角形T^q的3个顶点矢径，r^cp为场点三角形Tp的几何重心矢径。

对照图2-2所给的几何关系，令ρ_i=±(r′−r_i),i=1,2,3；±号的选择取决于感应电流从三角形顶点流出还是流入三角形顶点。因为每一个三角形对应于3个基函数，它们分别对应于矢量ρ_i,i=1,2,3 。定义A_i^pq为源点三角形Tq在感应电流沿ρ_i方向时在场点三角形T^p的重心r^cp处产生的矢量位；φ_i^pq为源点三角形T^q在场点三角形Tp的重心r^cp处产生的标量位。表达式为

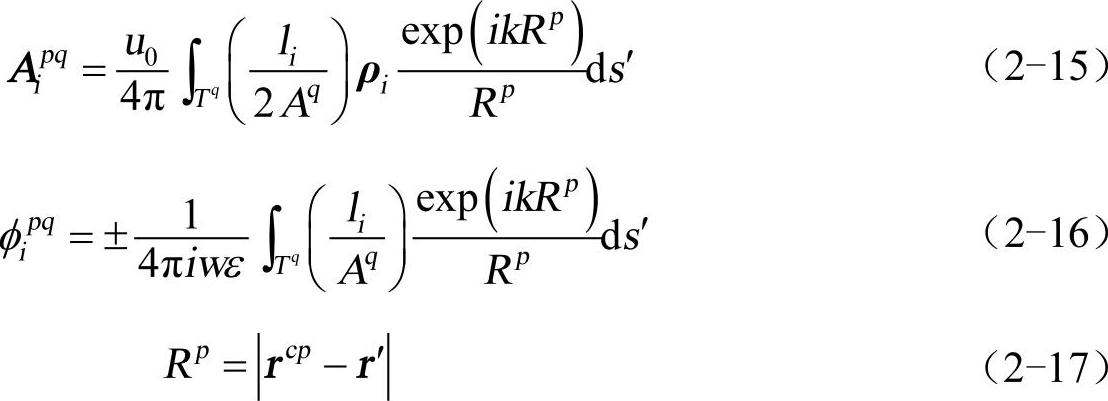
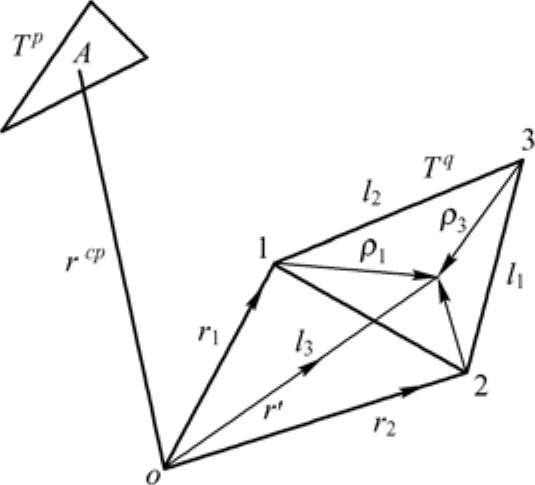
图2-2 全局坐标系中的场点三角形和源点三角形示意图

为方便三角形面积分建立以源三角形Tq的顶点1为坐标中心的局部坐标系，要求该三角形顶点1、2、3逆时针排列，如图2-3所示。定义归一化面积坐标变量：ξ、η、ς，定义如下

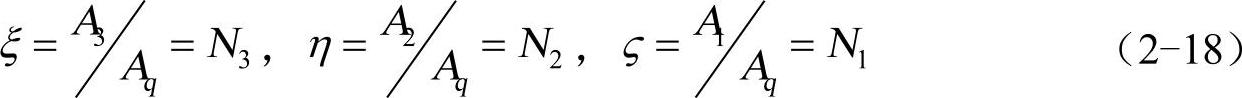
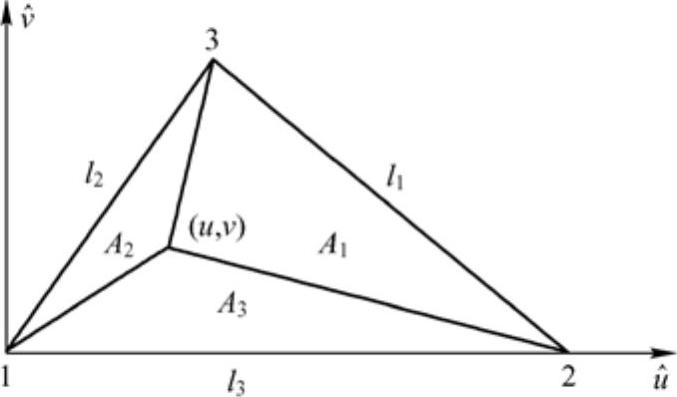
图2-3 局部坐标系中的三角形，顶点1、2、3逆时针排列

对应于图2-3中三角形上的任一点r′均可用该三角形的顶点坐标r₁,r₂,r₃表示为

r′=ςr₁+ηr₂+ξr₃=N₁r₁+N₂r₂+N₃r₃ （2-19）

利用ρ_i=±(r′−r_i),i=1,2,3和式（2-19），可以得到

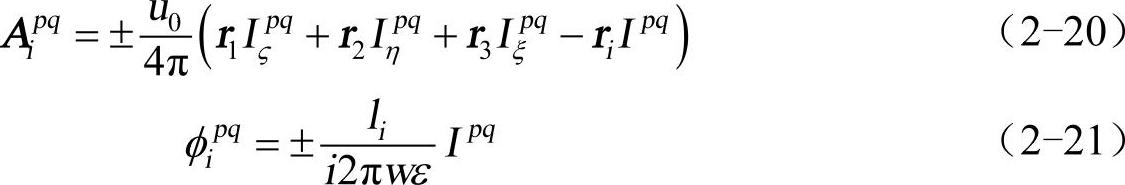
其中：

由此，阻抗元素的计算便归结为上式的计算。由此可见，利用平面三角对组合方法只需求出3个积分I^pq、I_ξ^pq、I_η^pq ，便可方便地求出该三角形所对应的3个基函数单元的积分值。对于I^pq、I_ξ^pq、I_η^pq，可利用Rogrila的方法进行计算。

当p≠q时，场点在源三角形外，式（2-22）～式（2-25）积分无奇异性，可用高斯积分计算，计算式如下

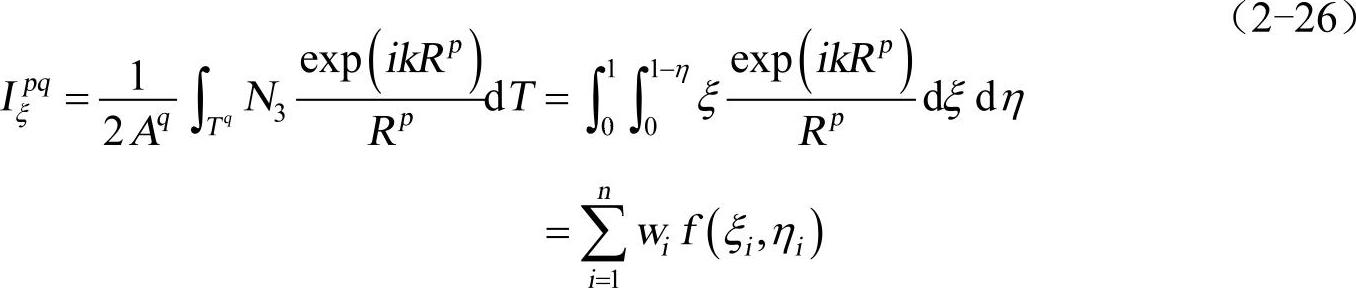
式中，n为高斯积分点数；w_i为权系数；函数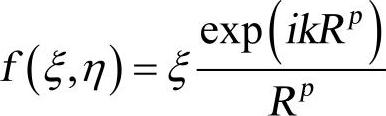。关于权系数w_i、结点(ξ_i,η_i)可采用九点等权高斯积分或七点不等权高斯积分计算。I^pq,I_η^pq计算类似。

当p=q时，场点在源三角形内，式（2-22）～式（2-25）积分有奇异性，必须用加减奇异项的方法处理。首先考虑式（2-24）的计算。

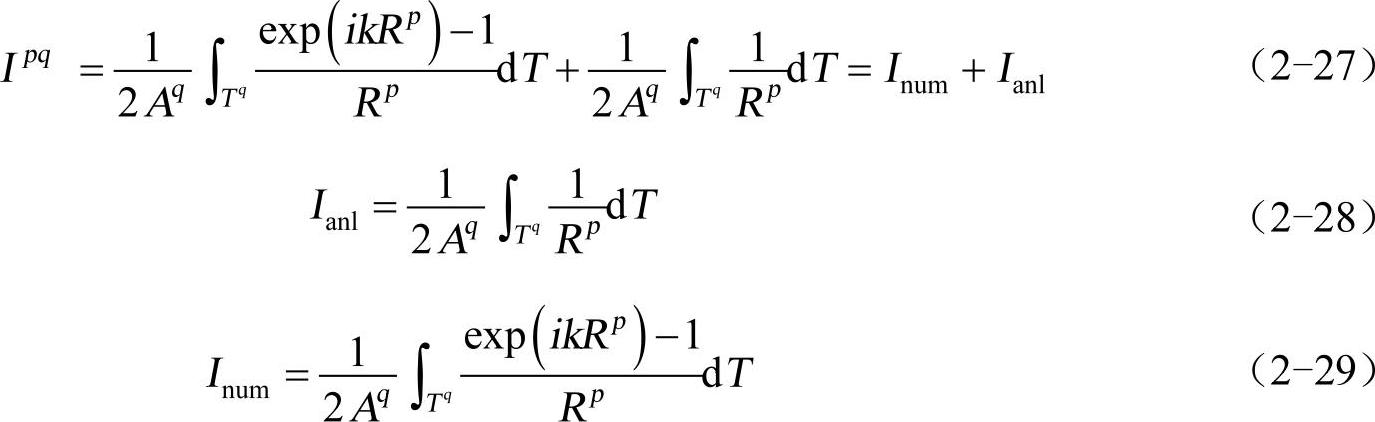
式（2-29）的计算用高斯积分易于计算，因为积分核已连续变化，并无奇异性。式（2-28）的积分有解析结果。

3.线性方程组的求解

通过矩量法把表面积分方程离散化为阻抗矩阵方程后，面临的问题是如何求解这一满阵的矩阵方程。对阻抗矩阵方程的数值求解有直接法和迭代法之分。直接方法的好处是对于小阶数矩阵的求解快速准确。但是当矩阵阶数增加时，计算复杂性随阶数的立方次增加。而好的迭代法的计算复杂度则是矩阵阶数的平方。因此，迭代求解法更能高效地求解阻抗矩阵方程。

（1）直接求解方法

直接方法的理论基础比较成熟。常用的直接法有高斯消元，LU分解求逆，SVD分解求逆等。由于LU分解所生成的逆矩阵刚好覆盖原矩阵，是一种节约内存的方法，因此LU分解是最常用的直接求逆方法。SVD分解求逆主要用于求解矩阵的广义逆，这适用于对病态矩阵或矩阵秩小于矩阵阶数的矩阵进行求逆。

（2）迭代求解法

当矩阵的阶数很大时，在给定的计算条件下用直接求逆求解矩阵方程将变得十分费时。所以需要寻求一种不用求逆的矩阵方程求解方案，这就是迭代法。常用的迭代法有：雅可比迭代法、高斯-塞德尔迭代法、超松弛迭代法、共轭梯度法及其改进、双共轭梯度法等。

FEKO仿真原理的实现和应用

相关推荐