对于稳定性试验所获得不同保管条件下不同考察周期的样品测试结果,通常需要利用统计方法检验其准确度是否发生了显著变化。通常,稳定性检验的统计方法包括t检验法、多重比较法等。按照多重比较统计方法进行稳定性试验设计和结果评价时,首先需要确定每个处理中所需样本份数。......
2023-06-29
上述F检验是一种整体性质的检验。若F检验显著或极显著,否定了无效假设H0,接受了HA,只是表明了总体上试验的各个处理平均数间存在显著或极显著差异,但并不意味着所有处理平均数两两之间都存在差异。如果试验的目的需要了解哪些处理间存在真实差异,那么就需要判断各处理平均数两两之间的差异显著性,也就需要进行进一步的多重比较(multiple comparisons),即多个平均数的两两比较。
多重比较的方法有很多,分为LSD法和LSR法,LSR法又分为SSR 法和q法,而SSR法在动物科学类专业中运用范围更广,q法与SSR法步骤相同,只不过参数不同,因此本部分介绍LSD法和SSR法。
1.LSD法(Least-Significant Difference)
LSD法(最小显著性差异法),是Fisher 于1935年提出的。其实质在于用T 检验原理完成各组间的配对比较。LSD 检验的敏感性高,各个水平间的均值存在微小的差异也有可能被检验出来。LSD多重比较基本步骤为:
(1)在F检验显著或极显著前提下,先计算出显著水平为α的最小显著差数LSDα;
LSDα的计算公式如下:
公式(3-8)中![]() 为F检验的误差自由度为dfe、显著水平为α(通常采用0.05或0.01)的临界t值,可以根据dfe,从t值表中查询得到显著水平为α(0.05 和0.01)的临界t值
为F检验的误差自由度为dfe、显著水平为α(通常采用0.05或0.01)的临界t值,可以根据dfe,从t值表中查询得到显著水平为α(0.05 和0.01)的临界t值![]() 。
。
![]() 为均数差数标准误,其计算公式如下:
为均数差数标准误,其计算公式如下:
(2)将任意2个处理平均数差数的绝对值![]() 与LSDα进行比较:若
与LSDα进行比较:若![]() ,则表示2个处理观测值总体平均数之间在α水平(0.05或0.01)上差异显著,即比较的2个处理组间存在差异。(www.chuimin.cn)
,则表示2个处理观测值总体平均数之间在α水平(0.05或0.01)上差异显著,即比较的2个处理组间存在差异。(www.chuimin.cn)
在进行LSD法进行多重比较时,可列出平均数多重比较表,表中α个处理平均数从大到小自上而下排列,计算并列出两两处理平均数的差数,然后与上面计算的LSDα进行比较,作出统计推断。如果在α=0.05 水平上显著,则在该差数右上方标记“*”,如果在α=0.01水平上显著,则在该差数右上方标记“**”。
2.SSR法(shortest significant ranges)
SSR 法,是邓肯(Duncan)于1955年提出的,又称为Duncan 法,亦称新复极差法(New multiple method)。SSR法多重比较基本步骤为:
(1)在F 检验显著或极显著前提下,先计算出显著水平为α的最小显著极差数![]() 的计算公式如下:
的计算公式如下:
公式(3-10)中![]() 是根据显著水平为α(通常采用0.05 或0.01)、误差自由度dfe、秩次距k,从SSR值表查出的临界SSR值。S
是根据显著水平为α(通常采用0.05 或0.01)、误差自由度dfe、秩次距k,从SSR值表查出的临界SSR值。S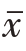 为均数标准误,其计算公式为:
为均数标准误,其计算公式为:
通过计算均数标准误S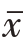 ,根据误差自由度dfe、秩次距k,从SSR值表查出显著水平为0.05、0.01的临界SSR值
,根据误差自由度dfe、秩次距k,从SSR值表查出显著水平为0.05、0.01的临界SSR值![]() ,将其乘以S
,将其乘以S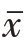 ,得到各个最小显著极差值
,得到各个最小显著极差值![]() 。
。
(2)列出平均数多重比较表,将平均数多重比较表中各个极差分别与对应的![]() 进行比较,作出统计推断。
进行比较,作出统计推断。
在方差分析判断试验资料数据所考察的指标整体上差异显著的基础上,进行多重比较分析,可以进一步明确考察的指标(不同处理)两两之间是否显著差异。
有关生物统计附试验设计实训的文章

对于稳定性试验所获得不同保管条件下不同考察周期的样品测试结果,通常需要利用统计方法检验其准确度是否发生了显著变化。通常,稳定性检验的统计方法包括t检验法、多重比较法等。按照多重比较统计方法进行稳定性试验设计和结果评价时,首先需要确定每个处理中所需样本份数。......
2023-06-29

第一步,建立假设检验;无效假设H0:属性类别分配符合已知属性类别分配的理论或学说;备择假设HA:属性类别分配不符合已知属性类别分配的理论或学说。第三步,确定P值并作出推断结果;若属性类别数为k,则适合性检验的自由度为k-1。表明属性类别分配与已知属性类别分配的理论或学说差异显著,或者说属性类别分配显著不符合已知属性类别分配的理论或学说;若χ2≥χ20.01(k-1),P ≤0.01,否定无效假设H0,接受备择假设HA。......
2023-10-30

根据此特点,只要知道其中一个词的意义,我们就可以推断出另一个词的意义,这就是对应推断法,或称对仗推断法。该句为对仗句,“据”对“拥”,“固”对“地”,“地”是“地方”,名词,那么“固”也是名词,据此推断“固”为“险固的地方”。借助“良”推断“劲”应为形容词,进而解为“硬的、强有力的”。由前文的“灭”可推断后文的“族”也是“灭亡”。......
2023-11-22

回归直线的精确度由(6-2)可知,离回归平方和Q 越小,即值越小时,预测值y与实际值y值越接近,目标回归直线的预测精确性越高。......
2023-10-30

测筒充砂密度,应按下列步骤进行测定:①准备不少于5000g的清洗干净的干燥标准砂。与此同时,不断向漏斗中补充标准砂,使砂面始终保持与漏斗上口齐平。充砂法试验应按下列步骤进行:①切取冻土试样。试样杯周侧包裹5cm厚的泡沫塑料保温,将其放入土工冻胀试验箱。调节土工冻胀试验箱箱体温度为-3℃,保持恒温。......
2023-10-02

如果F 检验的结论是拒绝H0,则说明因素A 的r 个水平有显著差异,也就是说,r 个均值之间有显著差异.但这并不意味着所有均值之间都有显著差异,这时还需要对每一对μi 和μj 作一一比较.通常采用多重t检验方法进行多重比较.这种方法本质上就是针对每组数据进行t检验,只不过估计方差时利用的是全部数据,因而自由度变大.具体地说,要比较第i组和第j 组均值,即检验H0:μi=μj,i≠j,i,j=1,2,…......
2023-11-18

通假推断法也称声训推断法,是运用声训原理以本义去释借义的方法。“今若遣此妇,终老不复取”中的“取”字,释为“争取、夺取”都讲不通,以“娶”代之则通,可推断为“取”通“娶”。“徇”通“殉”,义为“为了某种目的而死”,联系上下文,可以推断两个“徇”属同一义项,即“为……而死”。“涂”通“途”,义为“路途”“道路”,联系上下文,可以推断“涂”义为“道路”。特别提醒的是,并非所有同音字都能够通假。......
2023-11-22

结构推断法也叫语法分析法,就是分析所要解释的词在句中充当什么成分,然后根据成分推断其词性,进而推断其意义。C 句中“信张仪”是个动宾结构,因而断定“信”为“相信”义。运用结构推断法,还有助于认识词类的活用,我们判断一个词是否活用主要就是依据语法结构。......
2023-11-22
相关推荐