复变函数导数的定义在形式上与一元实变函数一致.定义1 设函数w = f(z)在点z0的某个邻域内有定义,且z0+△z是该邻域中的点,如果极限存在,我们称f(z)在点z0处可导(或可微),并称此极限值为f(z)在z0 点处的导数,记作若函数w = f(z)在点z0可导,导数为f′(z0),那么对于任意给定的ε ＞0,相应地存在δ(ε)＞0,使得当0 ＜|△z|＜δ时,有若函数w =f(z)在区域D内......
2025-09-30
拉氏变换性质|复变函数及应用
【摘要】：这一节将介绍拉氏变换的几个基本性质,它们在拉氏变换的实际应用中都是很有用的.为了叙述方便,假定在这些性质中,凡是要取拉氏变换的函数都满足拉氏变换存在定理中的条件,并且把这些函数的增长指数统一地设为c.在证明这些性质时,不再重复这些条件.1.线性性质设α,β为常数,且则有或2.相似性质设a ＞0,若L[f(t)]=F (p),则类似有以上两条性质的证明与傅氏变换相应的性质的证明是一样的.3.微分性质
这一节将介绍拉氏变换的几个基本性质,它们在拉氏变换的实际应用中都是很有用的.为了叙述方便,假定在这些性质中,凡是要取拉氏变换的函数都满足拉氏变换存在定理中的条件,并且把这些函数的增长指数统一地设为c.在证明这些性质时,不再重复这些条件.
1.线性性质
设α,β为常数,且
则有
或
2.相似性质
设a ＞0,若L[f(t)]=F (p),则
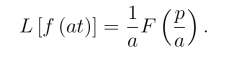
类似有
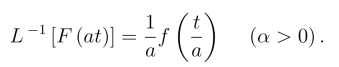
以上两条性质的证明与傅氏变换相应的性质的证明是一样的.
3.微分性质
设L[f(t)]=F (p),L[f′(t)]存在,则
证明
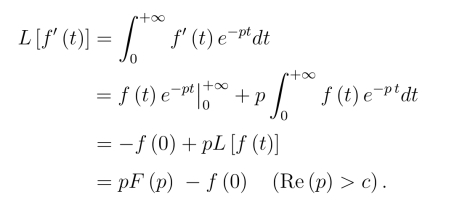
推论设
存在,则
特别当f(0)=f′(0)=···=f(n-1)(0)=0 时,有
由拉氏变换存在定理的结论(8.1.2)式,可得如下象函数的微分性质,即
设L[f(t)]=F (p),则
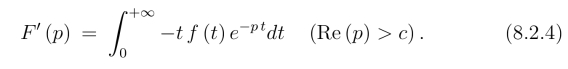
更一般有
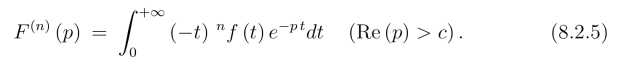
例1 利用线性性质求函数f(t)=ch(kt) 的拉氏变换.
解
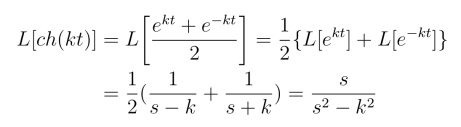
同理可得
例2 求L[cos kt](其中k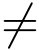 
0).
解 f(t)=cos kt,则
且f(0)=1,f′(0)=0.由微分性质,得
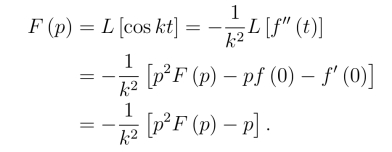
由此式可解出
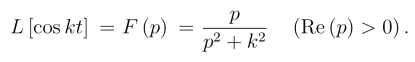
例3 利用微分性质求f(t)=tm的拉氏变换(m 为非负整数).
解 因为
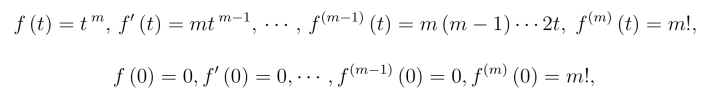
而
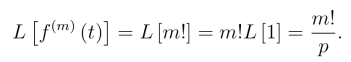
由拉氏变换微分性质(8.2.3),得
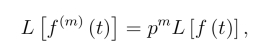
即
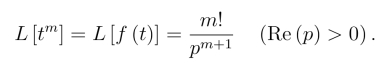
这个结果与§1例4的结果一致.
例4 求函数f(t)=t sin kt的拉氏变换.
解 因为L[sin kt]=
由象函数的微分性质可得
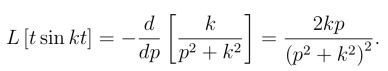
同理可得
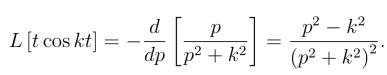
4.积分性质
若L[f(t)]=F (p),则
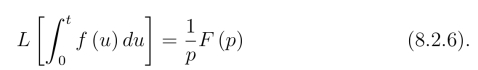
证明 设g(t)=
则有
且g(0)=0.由拉氏变换的微分性质(8.2.1)式
即
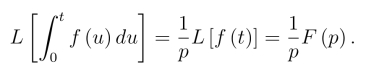
由拉氏逆变换存在定理,可以得到象函数的积分性质,
若L[f(t)]=F (p),则
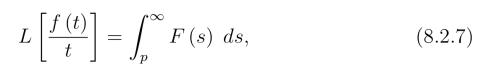
或
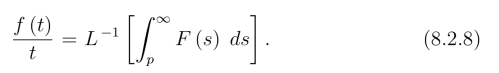
特别是当
存在时,在(8.2.7) 中,令p=0可得
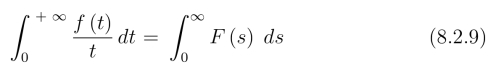(https://www.chuimin.cn)
(8.2.9)给我们提供了一种求反常积分的办法.
例5 求
解 因为L[sin t]=
由象函数的积分性质(8.2.7),得
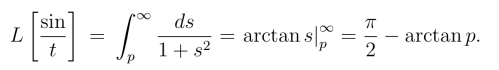
即
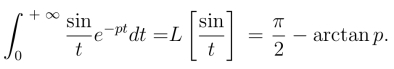
在上式中令p=0,得
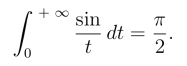
这个结果与第七章§1例1一致.
例6 求积分
解 由(8.2.9)
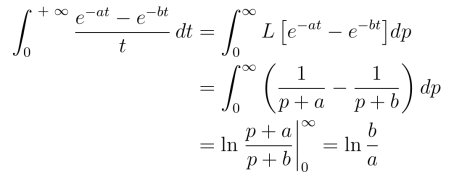
5.延迟性质
若L[f(t)]=F (p),又t ＜0时,f(t)=0,则对任一非负实数t0,有
或
证明 由拉氏变换定义
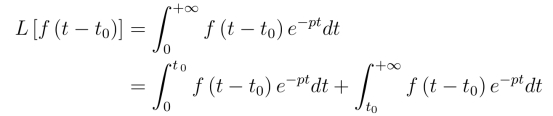
由t ＜0时f(t) = 0,得上式右端的第一个积分为零.对第二个积分,令u =t-t0,得
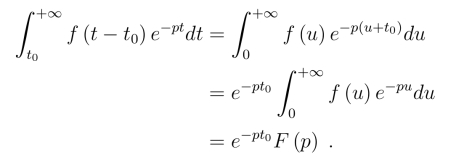
因此
延迟性质也称时移性质.f(t-t0) 与f(t)相比,f(t)是从t = 0开始有为非零数值,而f(t-t0)是从t = t0 开始才有为非零数值,即延迟了一个时间t0.如图8-1.
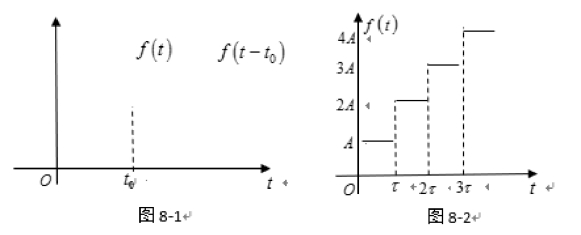
在本章第一节有过约定t ＜0时,f(t)=0,即f(t)应理解为f(t)u(t).这样延迟性质的公式(8.2.10)
应理解为
(8.2.11)式
应理解为
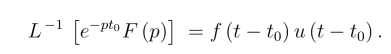
关于这个问题,我们还会在本章评注中通过例题进一步说明.
例7 求函数u(t-t0)=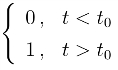
的拉氏变换.
解 因为
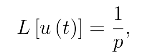
由延迟性质,得
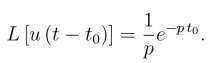
例8 求如图8-2所示的阶梯函数f(t)的拉氏变换.
解 利用单位阶跃函数,将f(t)表为
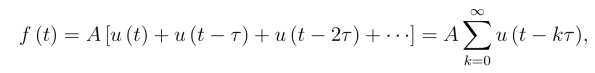
两边取拉氏变换,并假定右边的拉氏变换可以逐项进行.事实上,对满足拉氏变换存在定理条件的函数f(t)及τ ＞0,都有
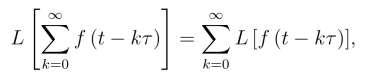
得
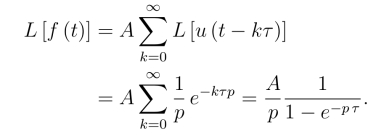
例9 求f(t)=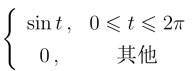
的拉氏变换.
解 因为f(t)可以改写为
而
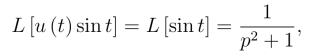
由线性性质及延迟性质,得
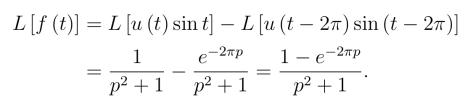
例10 设f(t)=(t-1)2,试求f(t)的拉氏变换.
解 因为f(t)=(t-1)2 =t2-2t+1,所以
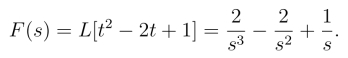
6.位移性质
若L[f(t)]=F (p),则有
证 由定义
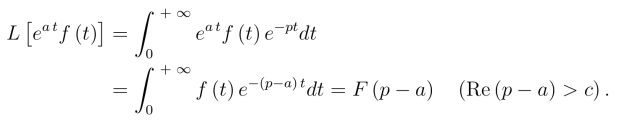
例11 求L[e-p0 t cos kt] 和L[e-p0 ttn].
解 由
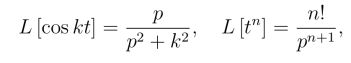
利用位移性质,得
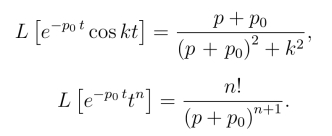
例12 求
解
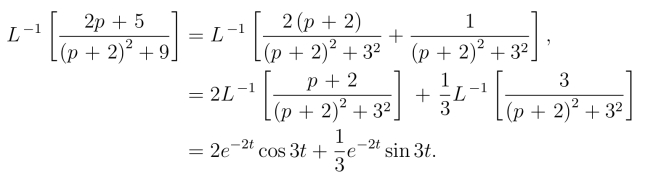
相关文章
- 详细阅读
-
复变函数与应用-复变函数及其应用详细阅读
幂函数w =zn(n ≥2为自然数)在z平面上处处可导,且除去原点外导数不为零,因此,在z平面上除去原点外是处处保角的.下面讨论w = zn在原点的性质.若令z = reiθ,w = ρeiφ,则由ρeiφ =rnelnθ,得由此可知,在w = zn映射下,z平面上的圆周|z| = r映射成w 平面上的圆周|w|=rn,射线arg z =θ0 映射成射线arg w =φ=nθ0,正实轴θ =0映射......
2025-09-30
-
解析函数概念|复变函数及应用详细阅读
解析函数是指在某个区域内可导的函数,它在理论和实际问题中应用广泛,具体定义如下：定义2 若函数f(z)在点z0的某个邻域内(包含点z0)处处可导,我们称f(z)在点z0处解析,也称它在z0全纯或正则,并称z0 是f(z) 的解析点,若函数f(z)在点z0处不解析,则称点z0 是f(z)的奇点; 若函数f(z)在区域D内的每一点都解析,则称函数f(z)在区域D内解析,或称f(z)是区域D内的解析函数......
2025-09-30
-
复积分基本性质详解-复变函数及其应用详细阅读
从复积分的定义,可以推得复积分具有下列基本性质,它们与实变函数中定积分的性质类似.若复变函数f(z)和g(z)沿其积分路径C可积,则有1° f(z)±g(z)沿C可积,且有2° 对任意复数A=a+ib,函数Af(z)沿C可积,有3° f(z)沿C的反向曲线C-可积,且有4° (复积分对积分路径的可加性)若函数f(z)沿曲线Ck(k =1,2,··· ,n)可积,且C 由Ck依次连接而成,则f(z)......
2025-09-30
-
复变指数函数的定义及性质详细阅读
从上节例2可知,f(z)=ex(cos y+i sin y)在整个复平面上解析,且f′(z)=f(z).容易验证f(z1+z2) =f(z1)+f(z2),据此我们给出复变指数函数的定义.定义1 对任意的复数z =x+iy,定义指数函数为w =ex(cos y+i sin y),记作ez.显然,|ez|=ex ＞0,而Arg(ez)=y+2kπ(k为整数),从而ez 0.当z 取实数,即y = 0......
2025-09-30
-
复变函数中保交比性质的定义和应用详细阅读
定义1 由扩充复平面上4个有序的相异点z1,z2,z3,z4构成的比式称为它们的交比,记作(z1,z2,z3,z4).若4点中有一个为∞,应将包含此点的分子或分母用1代替,例如z1 =∞,则对于扩充z平面上4个有序的相异点z1,z2,z3,z4经整线性映射w =az+b,得到扩充w平面上的4个点w1,w2,w3,w4,由于即整线性映射具有交比不变性.同样可验证w =具有交比不变性.综上可知,分式线......
2025-09-30
-
复变函数函数性态-复变函数及其应用详细阅读
如果是极点,指出它的级.解 令ζ = 则由于g(ζ)在ζ = 0解析且g 0,所以ζ = 0是的简单极点,因此z = ∞是f 的简单极点.......
2025-09-30
-
复变函数及应用：平面点集、区域详细阅读
|z-1|＜|z+3|; -1 ＜arg z ＜-1+π;0 ＜arg(z-1)＜,且Rez ＜3; 2 ≤|z|≤3;Imz ≤2; |3z+i|＜3;|z+2|+|z-2|≤6; 1 ＜|z-i|＜3.解 是无界单连通区域； 是无界单连通区域； 是有界的单连通域； 有界的多连通闭区域； 是无界单连通闭区域； 有界单连通区域； 是有界闭区域,不是区域； 是有界多连通区域.......
2025-09-30
相关推荐