设D为一单连通域,z0为D中的一点.若f(z)在D内解析,那么函数在z0点不解析.下面考虑D内围绕z0的简单闭曲线C上积分的计算.根据闭路变形原理,该积分值等于沿任何一条围绕z0的简单闭曲线上的积分.既然沿围绕z0的任何简单闭曲线积分值都相同.那么我们就取以z0为中心,半径为δ的圆周|z-z0| = δ(取其正向)作为积分曲线C.由于f(z)的连续性,在C上的函数f(z)的值将随着δ的缩小而逐渐接......
2023-10-30
复变函数中的傅里叶积分公式
【摘要】：定理1(傅氏积分定理) 若函数f(x)在(-∞,+∞)内有定义,且满足(1)在任一有限区间上满足狄利克雷条件,即在任意区间内满足: 连续或只有有限个第一类间断点; 只有有限个极值点;(2)在无限区间(-∞,+∞)内绝对可积(即积分收敛),则在f(x)的连续点上有成立,而左端的f(t)在它的间断点t处,应以来代替.这个定理称为傅里叶积分定理,简称为傅氏积分定理,其中所列的条件是充分的,它的证明需要用
定理1(傅氏积分定理) 若函数f(x)在(-∞,+∞)内有定义,且满足
(1)在任一有限区间上满足狄利克雷条件,即在任意区间内满足: 连续或只有有限个第一类间断点; 只有有限个极值点;
(2)在无限区间(-∞,+∞)内绝对可积(即积分
收敛),则在f(x)的连续点上有
成立,而左端的f(t)在它的间断点t处,应以
来代替.
这个定理称为傅里叶积分定理,简称为傅氏积分定理,其中所列的条件是充分的,它的证明需要用到较多的基础理论,证明略.
利用欧拉公式还可以把傅里叶积分公式化为三角形式
考虑到积分
是w的奇函数,
是w的偶函数,从而
(7.1.3)又可以表为
若记
则(www.chuimin.cn)
可以看出傅氏积分(7.1.5)式及系数公式(7.1.4)与函数的傅氏级数及系数公式在形式上极其相似,所不同的是级数的累加是离散的,积分形式的累加是连续的.
当f(t)为偶函数时,
此时
称之为f(t)的余弦傅氏积分公式.
当f(t)为奇函数时,A(w)=0,B(w)=
此时
称之为f(t)的正弦傅氏积分公式.
若函数f(t)只在(0,+∞)上有定义,且满足傅氏积分定理的条件,则只要作函数的偶式延拓或奇式延拓,便可得到f(t)的余弦傅氏积分公式或f(t)的正弦傅氏积分公式.
例1 设函数f(t)=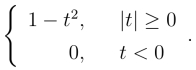
(1)求f(t)的傅里叶变换；
(2)计算
有关复变函数及其应用的文章
- 详细阅读
-
复积分在复变函数中的定义详细阅读
设C为平面上给定的一条光滑(或逐段光滑)曲线,则沿曲线C有两个方向,若选定其中的一个方向作为正方向,则称曲线C为有向曲线.设曲线C有两个端点A与B,若把从A到B的方向作为曲线C的正方向,则从B到A的方向就是C的负方向,记作C-.对于简单闭曲线,其正方向是指曲线上的点P沿此方向在该曲线前进时,邻近P点的曲线内部始终位于P点的左方,与之相反的方向就是曲线的负方向，而当曲线C为圆周时,逆时针方向就是曲线......
2023-10-30
-
形如的积分：复变函数及其应用详细阅读
定理2 设f(z)在实轴上解析,在上半平面Imz ＞0除有限个奇点z1,z2,··· ,zn 外解析.若存在正数r,M 和α ＞1,使当|z| ≥r 且Imz ≥0 时f(z)解析且满足|f(z)|≤M/|z|α,则积分I2 =存在且有证明设CR为上半圆周z = Reiθ(0 ≤θ ≤π),取充分大的R 使R ≥r并且奇点z1,z2,··· ,zn均在由CR及实轴上从-R 到R 的一段所围成的闭路......
2023-10-30
-
复变函数及其应用：形如的积分探讨详细阅读
定理3 设函数f(z)在实轴上无奇点,且在上半平面除有限个奇点z1,z2,··· ,zn外解析,若存在正数M和r,使当|z|≥r且Imz ≥0 时,函数f(z)解析且有则有证明 设CR为上半圆周: z = Reiθ(0 ≤θ ≤π),取充分大的R使R ≥r,并且奇点z1,z2,··· ,zn均在由CR 及实轴上从-R到R的一段所围成的半圆内,则由留数定理得只须证明当R →+∞时,上述沿CR 的积分......
2023-10-30
-
复变函数应用：高阶导数公式详细阅读
解析函数不仅有一阶导数,而且有各高阶导数,它的值也可以用函数在边界上的值通过积分来表示.但是对于一元实函数来说,它在某一区间上可导,其导数在这区域上是否连续也不一定,更不要说它有高阶导数存在了.关于解析函数的高阶导数我们有下面的定理.定理2 解析函数f(z)的导数仍为解析函数,它的n阶导数为其中C为在函数f(z)的解析区域D内围绕z0 的任何一条正向简单闭曲线,而且它的内部全含于D.证明 设z0为......
2023-10-30
-
柯西积分定理在复变函数应用中的成果详细阅读
由上一节复积分与实积分的关系式(3.1.2)可以看出,该复积分与路径无关的充要条件是其右端的两个对坐标的曲线积分都与路径无关.而平面上的曲线积分与路径无关的充要条件为:若函数P(x,y)和Q(x,y)在单连通域D内具有一阶连续偏导数,L为D内分段光滑的曲线,则曲线积分在D内与路径无关(或沿D内任意闭曲线的曲线积分为零)的充分必要条件是等式在D内恒成立.对于式右端的两个曲线积分,上述条件等式应当分别......
2023-10-30
-
复积分基本性质详解-复变函数及其应用详细阅读
从复积分的定义,可以推得复积分具有下列基本性质,它们与实变函数中定积分的性质类似.若复变函数f(z)和g(z)沿其积分路径C可积,则有1° f(z)±g(z)沿C可积,且有2° 对任意复数A=a+ib,函数Af(z)沿C可积,有3° f(z)沿C的反向曲线C-可积,且有4° (复积分对积分路径的可加性)若函数f(z)沿曲线Ck(k =1,2,··· ,n)可积,且C 由Ck依次连接而成,则f(z)......
2023-10-30
-
原函数与不定积分-复变函数及其应用详细阅读
由上一节定理2的推论,我们知道: 若函数f(z)在单连通区域D内处处解析,那么积分与连结起点及终点的路线C无关.设z0,z1 ∈D,解析函数在单连通域内的积分只与起点z0及终点z1有关,可记作固定z0,让z1在D内变动,并令z1 =z,那么积分在D内确定了一个单值函数F(z),即对于这个函数,我们有：定理1 若f(z)是单连通域D内处处解析,那么函数F(z)必为D内的一个解析函数,并且F′(z)=......
2023-10-30
相关推荐