保角映射的几个一般性定理应用

2023-10-30 理论教育版权反馈

【摘要】：在本章的前面,我们已经证明了解析函数在导数不为零的点处所构成的映射是保角映射,下面的定理指出,它的逆命题也成立.定理1 若函数w =f(z)是定义在区域D的保角映射,且将D一一对应地映射为区域G,则w = f(z)为D内的单叶解析函数,总有f′(z) 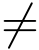0; 并且其逆映射z =φ(w)也是G内的单叶解析映射,且必有φ′(w)=1/f′(z)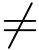0.由上面定理可以看出,双方单值的解析映射为保角映射,且保角

在本章的前面,我们已经证明了解析函数在导数不为零的点处所构成的映射是保角映射,下面的定理指出,它的逆命题也成立.

定理1 若函数w =f(z)是定义在区域D的保角映射,且将D一一对应地映射为区域G,则w = f(z)为D内的单叶解析函数,总有f′(z) pagenumber_ebook=197,pagenumber_book=188 0; 并且其逆映射z =φ(w)也是G内的单叶解析映射,且必有φ′(w)=1/f′(z)0.

由上面定理可以看出,双方单值的解析映射为保角映射,且保角映射的逆映射也一定是保角映射.

实际应用中经常需要求一个一一对应的保角映射,使扩充复平面上的单连通域映射为另外一个单连通域.扩充复平面上的单连通域的概念是有限复平面情形的推广.对有限复平面上的单连通域和多连通域,在扩充复平面上看来它们都是不包含点∞的区域,也分别称它们为单连通域和多连通域; 可是在扩充复平面上需要对包含点∞的区域D作些补充规定: 若区域D内任意一条简单闭曲线的内部点都属于D或外部点(包括点∞) 都属于D,则称D 为单连通域; 否则称D为多连通域.

因此,在扩充复平面上没有边界点的单连通域就是该扩充复平面; 只有一个边界点的单连通域只可能是除去有限点z0或点∞的区域,只有两个或三个边界点的区域一定是多连通域.

下面定理给出了使某个单连通域D一一对应地映射为单连通域G且具有保角性的映射惟一存在的条件.考虑到包含点∞的单连通域,如果它的边界点至少有一个点z0,那么可用在整个扩充复平面具有保角性的映射η = 1/(z-z0),使该单连通域对应地映射为不含点η =∞的单连通域.下面定理只讨论D和G不包含点∞的情形.

定理2(黎曼定理）若D和G是不包含点∞的单连域,其中它们的边界点都多于一个,则对任意给定的点z0 ∈D和w0 ∈G,以及实数θ0(-π ＜θ0 ≤π),一定存在唯一个在D内具有保角性的解析映射w =f(z)将D 一一对应地映射为G,且使

将上半平面一一对应地映射为单位圆的分式线性映射有无穷多个,其一般表达式中含有两个任意常数,要确定这些常数就需要给出含有它们的两个等式.由此可以看出式(6.4.1)中的这两个条件是不可少的; 其中f(z0)=w0的实部和虚部分别相等,以及arg f′(z0) = θ0可用来确定w = f(z)所依赖的三个实参数,使该映射是唯一的.(www.chuimin.cn)

黎曼定理并没有给出寻求这个映射函数w =f(z)的方法,但肯定了这种函数总是存在的.

定理3(边界对应原理）设有界单连通域D 和G的边界分别是简单闭曲线C 和Γ,C和Γ的绕向分别使D 和G保持在其边界的左侧,即它们都取正向.若函数w = f(z)在D 内解析,且在C上连续,w使C一一对应地映射为Γ,又使当动点z沿C的正向移动时,对应点w也沿Γ的正向移动,则w =f(z)在D内是保角的,且将D一一对应地映射为G.

f(z)在C上连续是指: 对于C上任意定点z0,当z从闭域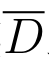 pagenumber_ebook=198,pagenumber_book=189 上趋向z0时,总有f(z)→f(z0).

实际中经常遇到D和G为无界的单连通域,它们的边界C和Γ都是分段光滑的简单闭曲线(包括曲线在点∞闭合的情形).这时,可取C和Γ的方向使D和G 分别保持在边界曲线绕向的左侧; 又可取z0和w0分别为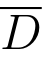 pagenumber_ebook=199,pagenumber_book=190 和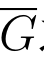之外的两个定点,利用分式线性映射将D和G 分别映射为有界单连通域D′和G′,其边界曲线可分别记为C′和Γ′.可以证明分式线性映射对这样的边界曲线也具有保侧性,即映射后C′ 和Γ′的方向也分别使D′和G′保持在其边界曲线的左侧.然后根据边界对应原理,利用满足该定理中边界条件的解析映射ξ = f(η),可使D′一一对应且保角地映射为G′.于是映射

的复合映射将w =φ(z)一一对应且保角地映射为G.

以上分析表明,对D和G为上述无界单连通域的情形,当w = f(z)在D内解析时,只要把定理中关于w = f(z)在C上连续的定义理解为对C上的点z0 =∞或使f(z0)=∞的点也适用,该定理仍然成立.

保角映射的几个一般性定理应用

相关推荐