幂函数w =zn(n ≥2为自然数)在z平面上处处可导,且除去原点外导数不为零,因此,在z平面上除去原点外是处处保角的.下面讨论w = zn在原点的性质.若令z = reiθ,w = ρeiφ,则由ρeiφ =rnelnθ,得由此可知,在w = zn映射下,z平面上的圆周|z| = r映射成w 平面上的圆周|w|=rn,射线arg z =θ0 映射成射线arg w =φ=nθ0,正实轴θ =0映射......
2023-10-30
解析函数导数的几何意义-复变函数及其应用
【摘要】：设w = f(z)在区域D内解析,z0 ∈D,且f′(z0) 0,C为z平面内通过点z0的一条有向光滑曲线（图6.3(a)):z0 =z(t0),且z′(t0)0,在映射w =f(z)下,C的象曲线Γ(图6.3(b)) 为：w(t0)=w0,Γ的正向为参数t增大的方向.根据复合函数的求导法则,有因此,在Γ上点w0处的切线存在,并且切线的正向与u 轴正向之间的夹角是即这表明,曲线Γ在w0 = f(z
设w = f(z)在区域D内解析,z0 ∈D,且f′(z0) 
0,C为z平面内通过点z0的一条有向光滑曲线（图6.3(a)):
z0 =z(t0),且z′(t0)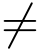
0,在映射w =f(z)下,C的象曲线Γ(图6.3(b)) 为：
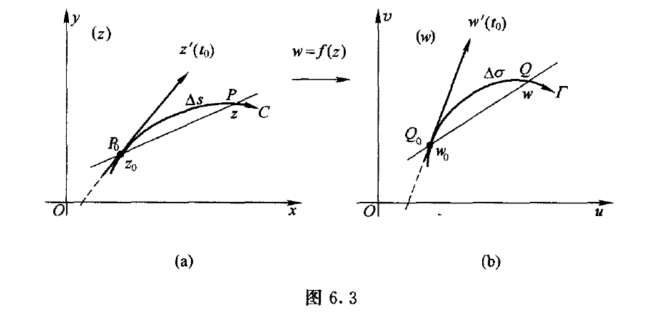
w(t0)=w0,Γ的正向为参数t增大的方向.
根据复合函数的求导法则,有
因此,在Γ上点w0处的切线存在,并且切线的正向与u 轴正向之间的夹角是
即
这表明,曲线Γ在w0 = f(z0) 处的切线方向,可看作由曲线C在z0处的切线方向旋转一个角度Argf′(z0) 得到.转动角的大小与方向只与z0 有关,而与过z0的曲线C的形状和方向无关.
现在假设曲线C1与C2相交于点z0,它们的参数方程分别是z = z1(t)与z = z2(t),α ≤t ≤β; 并且z0 = z1(t0) = z2(t′0),z′1(t0)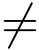 
0,z′2(t′0) 
0,α ＜t0 ＜β,α ＜t′0 ＜β.又设映射w = f(z)将C1与C2 分别映射为相交于点w0 = f(z0) 的曲线Γ1及Γ2,它们的参数方程分别是w = w1(t)与w =w2(t),α ≤t ≤β.由式(6.1.1),有
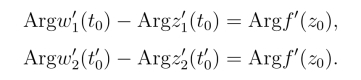
从而
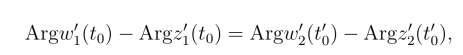
即
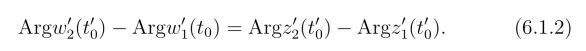(www.chuimin.cn)
上式两端分别是Γ1与Γ2以及C1与C2 之间的夹角,因此,
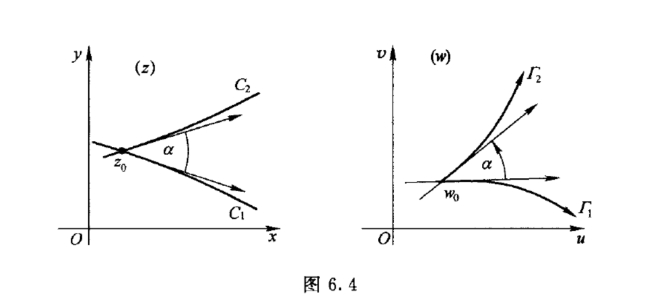
相交于点z0的任何两条曲线C1与C2之间的夹角,在其大小和方向上都等同于经过w =f(z)映射后跟C1 与C2 对应的曲线Γ1与Γ2之间的夹角(图6.4).所以这种映射具有保持两曲线间夹角的大小与方向不变的性质.这种性质称为保角性.
下面我们讨论函数f(z)在z0的导数的模|f′(z0)|的几何意义.
设z0 = z(t0),z = z(t0 + Δt),又设曲线C上从z0到z的曲线弧
在映射w = f(z) 下变为Γ上从点到w0到w的曲线弧
这两段弧长分别为Δs和Δσ(图6.3).
于是比值
可看作曲线C经过映射w = f(z)后对于曲线弧
的平均伸缩率.当z沿曲线C趋向z0时,称极限
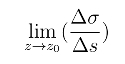
为曲线C经映射w =f(z)后在点z0的伸缩率.
由于
因此
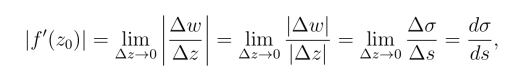
即
这样|f′(z0)|就是映射w = f(z)在点z0 的伸缩率,它只与z0有关,而与过z0的曲线C的形状和方向无关,这一性质称为伸缩率不变性.
综上,我们有:
定理1 设函数w =f(z)在区域D内解析,z0为D 内的一点,且f′(z0)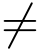
0,则映射w =f(z)在z0具有两个性质：
1)保角性 即通过z0的两条曲线间的夹角跟经过映射后所得两曲线间的夹角在大小和方向上保持不变.
2)伸缩率的不变性 即通过z0的任何一条曲线的伸缩率均为|f′(z0)|而与其形状和方向无关.
有关复变函数及其应用的文章
- 详细阅读
-
复变函数函数性态-复变函数及其应用详细阅读
如果是极点,指出它的级.解 令ζ = 则由于g(ζ)在ζ = 0解析且g 0,所以ζ = 0是的简单极点,因此z = ∞是f 的简单极点.......
2023-10-30
-
复变函数导数及应用-复变函数及其应用详细阅读
复变函数导数的定义在形式上与一元实变函数一致.定义1 设函数w = f(z)在点z0的某个邻域内有定义,且z0+△z是该邻域中的点,如果极限存在,我们称f(z)在点z0处可导(或可微),并称此极限值为f(z)在z0 点处的导数,记作若函数w = f(z)在点z0可导,导数为f′(z0),那么对于任意给定的ε ＞0,相应地存在δ(ε)＞0,使得当0 ＜|△z|＜δ时,有若函数w =f(z)在区域D内......
2023-10-30
-
解析函数概念|复变函数及应用详细阅读
解析函数是指在某个区域内可导的函数,它在理论和实际问题中应用广泛,具体定义如下：定义2 若函数f(z)在点z0的某个邻域内(包含点z0)处处可导,我们称f(z)在点z0处解析,也称它在z0全纯或正则,并称z0 是f(z) 的解析点,若函数f(z)在点z0处不解析,则称点z0 是f(z)的奇点; 若函数f(z)在区域D内的每一点都解析,则称函数f(z)在区域D内解析,或称f(z)是区域D内的解析函数......
2023-10-30
-
幂函数的规定及性质-复变函数及其应用详细阅读
定义3 设α是任意一个复数,定义幂函数为w =zα =eαLnz(z 0).在α为正实数时,对z =0的情况进行规定：zα =0.幂函数是指数函数与对数函数的复合函数,根据对数函数的定义,有w =zα =eαLnz =eα(ln z+2kπi) =eα ln z·e2αkπi,(k为整数)由于Lnz = ln z+2kπi是多值的,所以w = zα也是多值的,且所取的不同数值的个数等于e2αkπi......
2023-10-30
-
复变函数及其应用：对数留数详细阅读
函数f(z)关于闭曲线C的对数留数是指积分这里需要假定函数在C上解析.显然当C为简单正向闭曲线时,上述对数留数就是对数函数Lnf(z)的导数在C内部各个孤立奇点处留数之和.函数f(z)关于简单闭曲线C的对数留数与它在C内部的零点和极点的个数有密切的联系.即定理1 若函数f(z)在正向简单闭曲线C 上解析且没有零点,又在C的内部除有限个极点外解析,则有其中N与P分别是f(z)在C内部零点和极点的总个......
2023-10-30
-
保角映射概念解析-复变函数应用详细阅读
定义3 设函数w =f(z)在点z0的邻域内有定义,且在z0具有保角性和伸缩率的不变性,则称映射w = f(z)在z0点是保角映射,如果映射w = f(z)在区域内的每一点都是保角的,则称w =f(z)是区域内的保角映射.保角映射也称为保形映射或共形映射.在复变函数中还存在另一类保角映射,具有伸缩率的不变性,但仅保持夹角的绝对值不变而方向相反,称这种映射为第二类保角映射,从而相对地称定义3中所述的......
2023-10-30
-
复变函数及其应用：形如的积分探讨详细阅读
定理3 设函数f(z)在实轴上无奇点,且在上半平面除有限个奇点z1,z2,··· ,zn外解析,若存在正数M和r,使当|z|≥r且Imz ≥0 时,函数f(z)解析且有则有证明 设CR为上半圆周: z = Reiθ(0 ≤θ ≤π),取充分大的R使R ≥r,并且奇点z1,z2,··· ,zn均在由CR 及实轴上从-R到R的一段所围成的半圆内,则由留数定理得只须证明当R →+∞时,上述沿CR 的积分......
2023-10-30
相关推荐