利用路西定理比较两个函数的零点个数

2023-10-30 理论教育版权反馈

【摘要】：利用路西(Rouche)定理,我们能对两个函数的零点的个数进行比较.设函数f(z)和g(z)在简单闭曲线C上和C内解析,且在C上满足条件|f(z)|＞|g(z)|,则在C上有|f(z)| ＞0,|f(z) + g(z)| ≥|f(z)| - |g(z)| ＞0.从而在C上f(z)和f(z)+g(z)都不等于零.又设N和N′分别为函数f(z)与f(z)+g(z)在C 的内部的零点个数.由于这两个函数

利用路西(Rouch´e)定理,我们能对两个函数的零点的个数进行比较.

设函数f(z)和g(z)在简单闭曲线C上和C内解析,且在C上满足条件|f(z)|＞|g(z)|,则在C上有|f(z)| ＞0,|f(z) + g(z)| ≥|f(z)| - |g(z)| ＞0.从而在C上f(z)和f(z)+g(z)都不等于零.

又设N和N′分别为函数f(z)与f(z)+g(z)在C 的内部的零点个数.由于这两个函数在C 的内部解析,因此根据辐角原理有

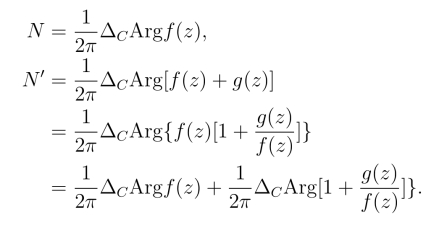
pagenumber_ebook=160,pagenumber_book=151

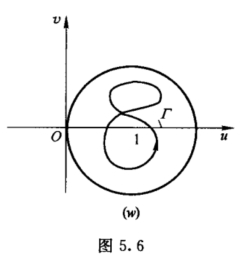
pagenumber_ebook=161,pagenumber_book=152

由于当z在C上时有|f(z)| ＞|g(z)|,因此点w = 1+ 总在|w-1| ＜1平面上的圆域|w-1| ＜1内(图5.6).于是当z在闭曲线C上连续变动一周时,动点w 在圆周|w-1|=1的内部画一封闭曲线Γ,它不围绕点w =0,故得

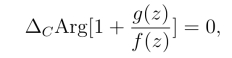
pagenumber_ebook=161,pagenumber_book=152

因此有

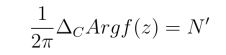
pagenumber_ebook=161,pagenumber_book=152

即N =N′,函数f(z)与f(z)+g(z)在C内的零点个数相同.于是我们得到

定理3(路西定理) 设f(z)与g(z)在简单闭曲线C上和C内解析,且在C上满足条件|f(z)|＞|g(z)|,则在C内f(z)与f(z)+g(z)的零点的个数相同.

路西定理是辐角原理的一个推论,在考査函数的零点分布时,用起来特别方便.路西定理也称为零点个数比较定理.

例2 试确定方程3z3-6z2+1=0在圆|z|＜1内以及在圆环1 ＜|z|＜3内根的个数.

解 (1)令f(z)=-6z2,g(z)=3z3+1.因为在|z|=1上有(www.chuimin.cn)

而函数f(z)在|z| ＜1内仅以z = 0为2级零点,所以由路西定理,方程f(z)+g(z)=3z3-6z2+1=0在|z|＜1内有2个根.

(2)令f(z)=3z3,g(z)=-6z2+1.因为在|z|=3上

pagenumber_ebook=162,pagenumber_book=153

而函数f(z)在|z|＜3内仅以z =0为3级零点,所以由路西定理,f(z)+g(z)=3z3-6z2+1=0在|z|＜3内有3个根,结合(1)可以得到该方程在1 ＜|z|＜3内只有1个根.

应用路西定理可以证明代数学基本定理.证明见下面例3.

例3 试证方程

有且仅有n个根.

证明设f(z)=a0zn,g(z)=a1zn-1+···+an-1z+an 因为

pagenumber_ebook=162,pagenumber_book=153

所以存在R ＞0,使当|z|≥R时有即|g(z)|＜|f(z)|.其中f(z),g(z)均在|z| ≤R上解析,且f(z) 在|z| ＜R内仅以z = 0为n 级零点.由路西定理,方程p(z) = f(z) + g(z) = 0在|z| ＜R内也有n个根; 另外当|z| ≥R时有|f(z)+g(z)| ≥|f(z)|-|g(z)| ＞0,这时方程p(z) = 0无根.从而方程p(z)=0有且仅有n个根.

利用路西定理比较两个函数的零点个数

相关推荐