以下我们来讨论两个总体的距离判别，分别讨论两个总体协方差矩阵相同和不同的情况．设总体X1 和X2 的均值向量分别为μ1 和μ2，协方差矩阵分别为Σ1 和Σ2．给定一个样本x，要判断x 来自哪个总体．首先考虑两个总体X1 和X2 的协方差矩阵相同的情况，即μ1 ≠μ2,Σ1＝Σ2＝Σ．要判断x 来自哪个总体，需要计算x 到总体X1 和X2 的马氏距离的平方d2（x，X1）和d2（x，X2），然后进行......
2023-11-18
用函数零点判别极点类型
【摘要】：如果是极点,指出它的级. f= f= f=解 f=的奇点是分母的零点.由于′ = cos z,而cos z在zk解析且cos zk 0,由定理2中的知zk 均为f的简单极点.易见z =1,z =-1是f的奇点.由于函数在z =1解析且因此z =1 是f 的三级极点.同理,z =-1是f的四级极点.z =0是f的极点,由于其中φ在z =0解析且φ0,z =0为f 的三级极点.
若函数f(z)在点z0解析且f(z0)=0,则称z0为函数f(z)的零点.
设函数f(z)在其零点z0的邻域|z-z0|＜δ内的泰勒级数为
则c0 =0,设m是使cm 
0的最小正整数,则
定义2 若函数f(z)在z0的邻域内的泰勒级数为
其中cm 
0,m为正整数,则称z0为f(z)的m级零点.
易见,z0为f(z)的m级零点的充分必要条件为存在解析函数φ(z),且φ(z0)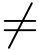
0,函数f(z) 在z0 的某邻域内能表示成
例如,z =1为f(z)=(z-1)2的2级零点.
另外,我们还可以通过f(z)在点z0的导数的值给出z0为f(z)的m级零点的充分必要条件.
定理1 z0为函数f(z)的m级零点的充分必要条件为f(z)在z0解析,f(z0)=f′(z0)=···=f(m-1)(z0)=0且f(m)(z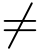0)
0.
证明 若z0为f(z)的m级零点,则f(z)在z0的邻域内的泰勒级数可展成式(5.1.3)的形式,对幂级数逐项求导,可得
反之,若f(z)在z0解析,f(z0)=f′(z0)=···=f(m-1)(z0)=0且f(m)(z0)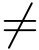
0,设f(z) 在z0 的邻域内的泰勒级数为
由系数公式知cn =
= 0(n = 0,1,2,··· ,m-1),而cm = 
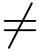0,即z0 为f(z) 的m 级零点.
下面给出用函数的零点判断极点的方法:
定理2 若函数f(z)和g(z)在点z0 解析,则有
(1) 当z0分别为f(z)和g(z)的m,n级零点时,z0为f(z)g(z) 的m+n级零点,若m ＜n,则有z0为
的n-m级极点.
(2) 当z0为g(z)的n级零点,但f(z0)
0时,z0为
的n 级极点.
证明(1)由于z0分别为f(z)和g(z)的m,n级零点,故存在函数φ(z)和ψ(z)在点z0解析,且φ(z0)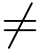
0,ψ(z0)
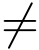0,使
从而有(www.chuimin.cn)
由式(5.1.4)和式(5.1.2)可知结论(1) 成立.
(2)设
则
由于
在点z0解析,且
故z0为
的n级极点.
在定理2的(2)中令f(z)=1可得
推论 若z0为g(z)的n级零点,则z0为
的n 级极点,反之也成立.
例1 下列函数有些什么奇点? 如果是极点,指出它的级.
(1) f(z)=
(2) f(z)=
(3) f(z)= 
解 (1)f(z)=
的奇点是分母的零点.
由于(sin z)′ = cos z,而cos z在zk解析且cos zk 
0(k = 0,±1,±2,···),由定理2中的(2)知zk(k =0,±1,±2,···) 均为f(z)的简单极点.
(2)易见z =1,z =-1是f(z)的奇点.由于
函数
在z =1解析且
因此z =1 是f(z) 的三级极点.
同理,z =-1是f(z)的四级极点.
(3)z =0是f(z)的极点,由于
其中φ(z)在z =0解析且φ(0)
0,z =0为f(z) 的三级极点.
有关复变函数及其应用的文章
- 详细阅读
-
用公式简化逻辑函数的方法详细阅读
一个逻辑函数的真值表是唯一的，但函数表达式可以有多种形式。对逻辑函数进行化简，求得最简表达式，可使实现逻辑函数的逻辑电路及问题的分析简单化，在工程上可以做到节省元器件、提高电路的可靠性。逻辑函数化简有公式法和卡诺图法两种。例如，逻辑函数式可以有五种表达式，其转换方法如下：原式是与或表达式。......
2023-06-24
-
如何判别螺纹的旋向及常见类型介绍详细阅读
螺纹的旋向也可用右手判别，判别时手心对着自己，四个手指沿螺杆中心线，然后看螺纹的旋向：如果螺纹的旋向与右手拇指的指向一致，则该螺纹为右旋螺纹，反之则为左旋螺纹，一般多用右旋螺纹。沿一条螺旋线所形成的螺纹称为单线螺纹，沿两条或两条以上的螺旋线所形成的螺纹称为多线螺纹。标准规定大径为螺纹的公称直径。也就是螺纹的最小直径，外螺纹用d1表示，内螺纹用D1表示。......
2023-06-25
-
辐角定理：复数变量s平面内的极点和零点辐角之详细阅读
s是复数变量，在s平面上可表示为s=σ+jω。不失一般性，取s平面上F的零点、极点及闭合路径，如图5-34所示。图5-34辐角定理示意图当s沿ΓS绕行时，∠和∠将随之变化。由式得式中，为F所有零点辐角之和；为F所有极点幅角之和。假设F在Γs之内有Z个零点和P个极点，当s沿Γs顺时针方向绕行一圈时，F的相角变化为相角变化-2π相当于ΓF按顺时针方向包围F平面的坐标原点一圈。......
2023-06-28
-
汽车机电维修工必读：车用灯具类型总结详细阅读
比如：1.照明设备灯前照灯前照灯俗称大灯，装在汽车头部的两侧，用于汽车在夜间或光线昏暗的路面上行驶时的照明，有两灯制和四灯制之分。装于车头的雾灯称为前雾灯，装于车尾的雾灯称为后雾灯。牌照灯牌照灯用来照亮汽车牌照，光色为白色。牌照灯安装在汽车牌照上部，一股采用5～10W的灯泡进行照明。当尾灯亮时，牌照灯也点亮。停车灯停车灯的功用是指示汽车夜间停放的位置。我国对各种汽车灯具的使用规定如表7-1所示。......
2023-08-26
-
黎曼1859论文：解析误差项和函数的关键非平详细阅读
黎曼1859的论文给出了误差项的精确表达式，这个表达式涉及了ζ函数的所有非平凡零点，因此，理解这个误差项的关键以某种方式隐藏在这些零点之中.零点在哪里？......
2023-11-19
-
利用路西定理比较两个函数的零点个数详细阅读
利用路西(Rouche)定理,我们能对两个函数的零点的个数进行比较.设函数f(z)和g(z)在简单闭曲线C上和C内解析,且在C上满足条件|f(z)|＞|g(z)|,则在C上有|f(z)| ＞0,|f(z) + g(z)| ≥|f(z)| - |g(z)| ＞0.从而在C上f(z)和f(z)+g(z)都不等于零.又设N和N′分别为函数f(z)与f(z)+g(z)在C 的内部的零点个数.由于这两个函数......
2023-10-30
-
复数项级数的收敛性及判别法-书籍《复变函数及详细阅读
设{αn}={an+ibn}(n=1,2,···) 为一复数列,表达式称为无穷级数,其前n项的和称为级数的部分和.若该部分和数列收敛,其极限为S,则称上述复数项级数收敛,且称S 为该级数的和,记为若部分和数列{Sn}发散,则称级数发散.定理4 级数 收敛的充要条件是其实部级数和虚部级数都收敛.证明 因其中σn =a1+a2+···+an,τn =b1+b2+···+bn 分别为 的部分和.由定理2......
2023-10-30
相关推荐