若f(z)在圆环域R1 <|z-z0|<R2内解析,C 为圆环域内绕z0的正向简单闭曲线,则f(x)在该圆环域内的洛朗展开式为其中因而可以将复积分的计算转化为求被积函数的洛朗展开式中(z-z0)的负一次幂项的系数c-1.例4 计算积分解 函数f(z)= 在1 <|z|<∞内解析,|z|=3 在此圆环域内,把它在此圆环域内展开得故从而例5 计算积分解 先分析函数的解析性.令ζ = 由于ln ζ的不解......
2023-10-30
1.直接展开法
从上面定理可以看出,若函数f(z)在点z0解析,从而在该点某个邻域内也解析,则其展开式(4.3.1) 在该邻域内成立,并且可以利用所给函数f(z)的奇点得到幂级数(4.3.1) 的收敛半径; 不必像把实变函数展开成泰勒级数那样验证其幂级数的余项RN(x) →0(N →∞),也不必再利用所得泰勒级数的系数求其收敛半径.所谓直接展开法是指先求出cn = ![]() 然后直接利用上面所给泰勒级数展开定理写出其泰勒级数展开式(4.3.1)及其收敛半径.
然后直接利用上面所给泰勒级数展开定理写出其泰勒级数展开式(4.3.1)及其收敛半径.
例如函数f(z) = ez,z0 = 0.由于函数f(z) 在整个复平面处处解析,因此它在点z0 = 0处的泰勒级数的收敛半径R = ∞.又因f(n)(0) = 1,所以由上面定理可直接写出它在点z0 =0 处的泰勒级数展开式为
同样可得,下列函数在z0 =0处的泰勒级数展开式分别为
例1 求对数函数的主值ln(1+z)在z =0 处的泰勒展开式.
解 我们知道,ln(1+z)在从-1向左沿负实轴剪开的平面内是解析的,而-1 是它的一个奇点,所以它在|z|<1 内可以展开成z的幂级数.
因为[ln(1+z)]′ =![]() 而
而
任取一条从0到z的积分路线C,将上式的两端沿C 逐项积分,得
即
这就是所求的泰勒展开式.
例2 求幂函数(1+z)a (a为复数)的主值:
在z =0处的泰勒展开式.
解 显然,f(z)在从-1起向左沿负实轴剪开的复平面内解析,因此必能在|z|<1内展开成z的幂级数.设
所以
求导,得
即
继续求导得
令z =0,得
所求展开式为
特别地α=-1时,有![]() =1+z+z2+z3+··· (|z|<1).
=1+z+z2+z3+··· (|z|<1).
2.间接展开法
借助一些已知函数的展开式,利用幂级数的运算性质和分析性质(上一节定理4),以惟一性为依据来得出一个函数的泰勒展开式.这种方法称为间接展开法.例如sin z在z =0的泰勒展开式也可用间接展开法得出:(www.chuimin.cn)
从而得出cos z在z =0的泰勒展开式为
例3 将函数f(z)=![]() 在z0 =-i处展开成泰勒级数.
在z0 =-i处展开成泰勒级数.
解 函数f(x)的奇点为i和0,距z0 =0最近的不解析点为原点,因此收敛半径R=1.由于
且
两式相减可得所求展开式为
例4 求f(z)=ez cos z在z =0处的泰勒展开式.
解
利用函数ez的泰勒级数展开式可得其展开式为
f(z)处处解析,其收敛半径R=∞.
例5 求f(z)=arctan z在z =0处的泰勒展开式.
解 解法1 由于
利用例1的结论,则有
解法2 因为
而
从而
由上一节的定理4和本节的定理知,幂级数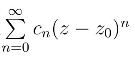 在收敛圆内|z -z0| <R 的和函数是解析函数; 反过来,在圆域|z -z0| <R 内解析的函数f(z)必能在z0展开成幂级数
在收敛圆内|z -z0| <R 的和函数是解析函数; 反过来,在圆域|z -z0| <R 内解析的函数f(z)必能在z0展开成幂级数![]() 所以,f(z)在z0解析跟f(z)在z0的邻域内可以展开成幂级数
所以,f(z)在z0解析跟f(z)在z0的邻域内可以展开成幂级数 是两种等价的说法.
是两种等价的说法.
例6 设f(z)=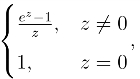 试证f(z)在点z0解析.并且求它在该点处的泰勒级数展开式及其收敛半径.
试证f(z)在点z0解析.并且求它在该点处的泰勒级数展开式及其收敛半径.
解 由于
等式两端除以z 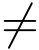 0得
0得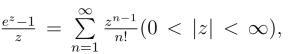 该式右端幂级数的收敛半径R = ∞,由上一节定理4,其和函数S(z)在整个复平面处处解析,且S(0) = 1 = f(0),于是在整个复平面有S(z) = f(z),f(z)在整个复平面解析,且有
该式右端幂级数的收敛半径R = ∞,由上一节定理4,其和函数S(z)在整个复平面处处解析,且S(0) = 1 = f(0),于是在整个复平面有S(z) = f(z),f(z)在整个复平面解析,且有
这就是f(z)在点z0的泰勒级数展开式,且R=∞.
有关复变函数及其应用的文章

若f(z)在圆环域R1 <|z-z0|<R2内解析,C 为圆环域内绕z0的正向简单闭曲线,则f(x)在该圆环域内的洛朗展开式为其中因而可以将复积分的计算转化为求被积函数的洛朗展开式中(z-z0)的负一次幂项的系数c-1.例4 计算积分解 函数f(z)= 在1 <|z|<∞内解析,|z|=3 在此圆环域内,把它在此圆环域内展开得故从而例5 计算积分解 先分析函数的解析性.令ζ = 由于ln ζ的不解......
2023-10-30

泰勒多项式:如果f(x)在点x0的某邻域内具有各阶导数,则在该邻域内f(x)近似等于其中(ξ介于x与x0之间).如果f(x)存在任意阶导数,且的收敛半径为R,则于是成立的充分必要条件是:当|x-x0|<R时,,即下面定理成立.定理 设函数f(x)在点x0的某一邻域U(x0)内具有各阶导数,则f(x)在该邻域内能展开成泰勒级数的充分必要条件是f(x)的泰勒公式中余项Rn(x)当n→∞时极限为零,即麦......
2023-10-19

对于收敛圆的圆心相同的两个复数项幂级数,它们的四则运算可以像实数项幂级数那样来进行,要根据其系数来确定.对于和、差、积所得幂级数在其公共收敛圆内显然收敛,其收敛半径不会小于所给级数的收敛半径最小的一个.如对乘积运算若上式左端两个幂级数的收敛半径分别为R1和R2,则其积的幂级数收敛半径R >min{R1,R2}.为了说明两个幂级数经过运算后所得的幂级数的收敛半径确实可以大于R1 和R2 中较小的一个......
2023-10-30

而对于另外一些函数,比如对数函数,某一点的泰勒级数只能用于近似计算该点附近小范围区间内的各点函数值。参考阅读//No. 4 极限,第12页No. 23 多项式,第50页No. 24 对数,第52页No. 50 导数,第104页右图:正弦函数不是多项式,但是它在0处的泰勒级数是个有着无穷多项的多项式,随着我们算的项越来越多,对x=0处的函数值的近似计算就会越来越精确。......
2023-11-22

在本章开始时,我们曾考查过一种较简单的级数——等比级数.其每一项都是x的函数,由此,我们给出函数项级数的概念.一、函数项级数的一般概念设有定义在区间I上的函数列由此函数列构成的表达式称作函数项级数.函数项级数的所有收敛点的全体称为它的收敛域(收敛区间);函数项级数的所有发散点的全体称为它的发散域(或发散区间).在函数项级数中,函数项级数中最常见的一类级数是幂级数.二、幂级数及其收敛性下面我们讨论幂......
2023-11-20

对于一元实函数来说,若f(x)在点x0的某邻域内有任意阶的导数,并且在该邻域内恒有余项则f(x)在点x0的该邻域内的泰勒(Taylor)级数展开式为复变函数中,函数f(x)在点z0的某邻域内有任意阶导数等价于它在该邻域内解析,对于解析函数有下面的展开定理.定理1(泰勒级数展开定理) 若函数f(z) 在圆形区域D:|z-z0| <R内解析,则它在D内可展开为幂级数其中 若C为D内绕z0 的正向简单闭......
2023-10-30

泰勒是西方古典管理理论的主要代表人物之一,同时也是科学管理理论的创始人。1890年,泰勒离开米德维尔钢铁厂,先后担任过投资公司总经理,从事过工厂的管理咨询工作。1906年,泰勒担任了美国机械工程师协会的主席,1915年,在一次发表演讲的归途中,泰勒患上了肺炎,在刚度过59岁生日的第二天在医院病逝。......
2024-04-06
相关推荐