前面我们证明了在区域D内的解析函数,其导数仍为D内的解析函数,下面我们用这个结论来研究解析函数与调和函数的关系.定义1 若φ(x,y)在平面区域D内有二阶连续偏导数,并且满足拉普拉斯(Laplace)方程则称φ=φ(x,y)在D内为调和函数.引入记号称为Laplace算子,则式(3.5.1)可简记为△φ=0.定理1 若函数f(z)=u(x,y)+iv(x,y)在区域D内解析,则u=u(x,y)和v......
2025-09-30
同高等数学中的实变幂级数一样,复变幂级数也有所谓幂级数的收敛定理,即阿贝尔(Abel) 定理.
定理1(阿贝尔定理) 若级数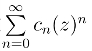 在z = z0(
在z = z0(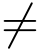 0) 收敛,那么对满足|z| <|z0| 的z,级数必绝对收敛.若在z = z0级数发散,那么对满足|z|>|z0| 的级数必发散.
0) 收敛,那么对满足|z| <|z0| 的z,级数必绝对收敛.若在z = z0级数发散,那么对满足|z|>|z0| 的级数必发散.
证明 若级数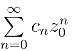 收敛,根据收敛的必要条件,有
收敛,根据收敛的必要条件,有![]() 因而存在正数M,使对所有的n有
因而存在正数M,使对所有的n有
若|z|<|z0|,则![]() 从而
从而
由于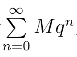 为公比小于1的等比级数,故收敛,根据正项级数的比较审敛法知
为公比小于1的等比级数,故收敛,根据正项级数的比较审敛法知
收敛,从而级数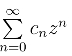 绝对收敛.
绝对收敛.
若级数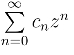 发散,|z1|>|z0| 且在z1 处级数收敛,则由上面的证明结果可知在z0(|z0|<|z1|) 处级数收敛,这与级数
发散,|z1|>|z0| 且在z1 处级数收敛,则由上面的证明结果可知在z0(|z0|<|z1|) 处级数收敛,这与级数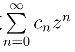 发散矛盾.(https://www.chuimin.cn)
发散矛盾.(https://www.chuimin.cn)
由阿贝尔定理知级数![]() 的收敛情况分为三种:
的收敛情况分为三种:
(1)仅在z =0处收敛,如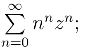
(2)在整个复平面内处处收敛,如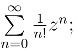
(3)在复平面上存在一点z0,在|z|<|z0|处收敛,在|z|>|z0| 时发散.
若令R=|z0|,则称圆周|z|=R为幂级数的收敛圆,在收敛圆的内部,级数绝对收敛,在收敛圆的外部,级数发散.收敛圆的半径R称为收敛半径.因此幂级数(4.2.3) 的收敛范围是以原点为中心的圆域.对幂级数(4.2.2)来说,它的收敛范围是以z =a为中心的圆域.在收敛圆的圆周上是收敛还是发散,要对具体级数进行具体分析.
相关文章

前面我们证明了在区域D内的解析函数,其导数仍为D内的解析函数,下面我们用这个结论来研究解析函数与调和函数的关系.定义1 若φ(x,y)在平面区域D内有二阶连续偏导数,并且满足拉普拉斯(Laplace)方程则称φ=φ(x,y)在D内为调和函数.引入记号称为Laplace算子,则式(3.5.1)可简记为△φ=0.定理1 若函数f(z)=u(x,y)+iv(x,y)在区域D内解析,则u=u(x,y)和v......
2025-09-30

解析函数是指在某个区域内可导的函数,它在理论和实际问题中应用广泛,具体定义如下:定义2 若函数f(z)在点z0的某个邻域内(包含点z0)处处可导,我们称f(z)在点z0处解析,也称它在z0全纯或正则,并称z0 是f(z) 的解析点,若函数f(z)在点z0处不解析,则称点z0 是f(z)的奇点; 若函数f(z)在区域D内的每一点都解析,则称函数f(z)在区域D内解析,或称f(z)是区域D内的解析函数......
2025-09-30

设z1 =r1eiθ1,z2 =r2eiθ2,··· ,zn =rneiθn是n个非零复数,用数学归纳法可以得到这n个复数的乘积为特别地,当这n个复数相同时,我们把n个相同的复数z的乘积称为z的n次幂,记作zn.设z =reiθ,则zn =rneinθ =rn(cos nθ+i sin nθ).当r =1时,即z =cos θ+i sin θ,有(cos θ+i sin θ)n =cos nθ+i......
2025-09-30

;写出幂级数,并求出收敛半径R;考查当x在区间内时余项Rn的极限是否为零.如果为零,则函数f在区间内的幂级数展开式为例1 将函数f=ex展开成x的幂级数.解 由fn=ex,得fn=1(n=0,1,2,…......
2025-09-30

由上一节定理2的推论,我们知道: 若函数f(z)在单连通区域D内处处解析,那么积分与连结起点及终点的路线C无关.设z0,z1 ∈D,解析函数在单连通域内的积分只与起点z0及终点z1有关,可记作固定z0,让z1在D内变动,并令z1 =z,那么积分在D内确定了一个单值函数F(z),即对于这个函数,我们有:定理1 若f(z)是单连通域D内处处解析,那么函数F(z)必为D内的一个解析函数,并且F′(z)=......
2025-09-30

定义3 设α是任意一个复数,定义幂函数为w =zα =eαLnz(z 0).在α为正实数时,对z =0的情况进行规定:zα =0.幂函数是指数函数与对数函数的复合函数,根据对数函数的定义,有w =zα =eαLnz =eα(ln z+2kπi) =eα ln z·e2αkπi,(k为整数)由于Lnz = ln z+2kπi是多值的,所以w = zα也是多值的,且所取的不同数值的个数等于e2αkπi......
2025-09-30

所谓复合闭路是指一种特殊的有界多连通域D的边界曲线Γ,它由几条简单闭曲线组成,可简记为Γ=其中简单闭路C取正向; 简单闭路取负向,它们都在C 的内部且互不相交又互不包含(图3.6).上述Γ 的方向称为多连域D的边界曲线的正向.定理3(复合闭路定理) 设D是以复闭路Γ = 为边界的多连通域.若函数f(z) 在D内及其边界Γ上解析,则f(z)沿Γ的积分为零.这时有证明 只须证n = 2的情形.在区域D......
2025-09-30

设C为平面上给定的一条光滑(或逐段光滑)曲线,则沿曲线C有两个方向,若选定其中的一个方向作为正方向,则称曲线C为有向曲线.设曲线C有两个端点A与B,若把从A到B的方向作为曲线C的正方向,则从B到A的方向就是C的负方向,记作C-.对于简单闭曲线,其正方向是指曲线上的点P沿此方向在该曲线前进时,邻近P点的曲线内部始终位于P点的左方,与之相反的方向就是曲线的负方向,而当曲线C为圆周时,逆时针方向就是曲线......
2025-09-30
相关推荐