解析函数是指在某个区域内可导的函数,它在理论和实际问题中应用广泛,具体定义如下：定义2 若函数f(z)在点z0的某个邻域内(包含点z0)处处可导,我们称f(z)在点z0处解析,也称它在z0全纯或正则,并称z0 是f(z) 的解析点,若函数f(z)在点z0处不解析,则称点z0 是f(z)的奇点; 若函数f(z)在区域D内的每一点都解析,则称函数f(z)在区域D内解析,或称f(z)是区域D内的解析函数......
2023-10-30
复变函数幂级数概念解析
【摘要】：回答是肯定的,下面更深入地讨论这个问题.
设{fn(z)}(n=1,2,...)为一复变函数序列,均在区域D内有定义.表达式
称为复变函数项级数,记作
这级数的前n 项的和
称为这级数的部分和.若将集合D中某一点z0代人级数(4.2.1)中使复数项级数
收敛,则称该函数项级数在点z0收敛,z0为级数(4.2.1) 的收敛点,其收敛点所构成的集合D0 为该级数的收敛域(D0 ⊆D不一定是区域).这时,对任意z ∈D0可记
S(z)称为级数
的和函数.当fn(z) = cn-1(z - a)n-1或fn(z) =cn-1zn-1 时,就得到函数项级数的特殊情形.
或
这种级数称为幂级数.若令z-a=ζ,则式(4.2.2)成为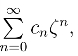
即式(4.2.3)的形式.因此只需要讨论式(4.2.3) 的幂级数.
例1 讨论幂级数(www.chuimin.cn)
的敛散性.
解 级数的部分和为
当|z| ＜1时,由于
即|z| ＜1 时,级数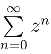
收敛,和函数为
当|z| ＞1时,由于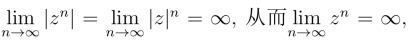
原级数发散.
当z =1时,则
原级数发散.综上得
在一般情况下,幂级数(4.2.3)是否存在一个圆周|z| = R,它在该圆外部发散且在其内部绝对收敛呢? 回答是肯定的,下面更深入地讨论这个问题.
有关复变函数及其应用的文章
- 详细阅读
-
保角映射概念解析-复变函数应用详细阅读
定义3 设函数w =f(z)在点z0的邻域内有定义,且在z0具有保角性和伸缩率的不变性,则称映射w = f(z)在z0点是保角映射,如果映射w = f(z)在区域内的每一点都是保角的,则称w =f(z)是区域内的保角映射.保角映射也称为保形映射或共形映射.在复变函数中还存在另一类保角映射,具有伸缩率的不变性,但仅保持夹角的绝对值不变而方向相反,称这种映射为第二类保角映射,从而相对地称定义3中所述的......
2023-10-30
-
复变函数及其应用：幂级数运算特性详细阅读
对于收敛圆的圆心相同的两个复数项幂级数,它们的四则运算可以像实数项幂级数那样来进行,要根据其系数来确定.对于和、差、积所得幂级数在其公共收敛圆内显然收敛,其收敛半径不会小于所给级数的收敛半径最小的一个.如对乘积运算若上式左端两个幂级数的收敛半径分别为R1和R2,则其积的幂级数收敛半径R ＞min{R1,R2}.为了说明两个幂级数经过运算后所得的幂级数的收敛半径确实可以大于R1 和R2 中较小的一个......
2023-10-30
-
复变函数与应用-复变函数及其应用详细阅读
幂函数w =zn(n ≥2为自然数)在z平面上处处可导,且除去原点外导数不为零,因此,在z平面上除去原点外是处处保角的.下面讨论w = zn在原点的性质.若令z = reiθ,w = ρeiφ,则由ρeiφ =rnelnθ,得由此可知,在w = zn映射下,z平面上的圆周|z| = r映射成w 平面上的圆周|w|=rn,射线arg z =θ0 映射成射线arg w =φ=nθ0,正实轴θ =0映射......
2023-10-30
-
复变函数函数性态-复变函数及其应用详细阅读
如果是极点,指出它的级.解 令ζ = 则由于g(ζ)在ζ = 0解析且g 0,所以ζ = 0是的简单极点,因此z = ∞是f 的简单极点.......
2023-10-30
-
求幂级数和函数的解析详细阅读
【主要内容】1.求幂级数和函数的方法的和函数可按以下方法计算：（1）对进行适当的代数运算（例如，将的各项同乘以一个常数或xk，或者提出一个常数或xk，k为某个正整数），或作适当的变量代换，使其成为常用函数的麦克劳林级数，从而求得的和函数s（x）.有时将表示成几个幂级数之和，然后对每个幂级数都作以上处理，由此算得的和函数s（x）.（2）对在收敛区间内进行求导或积分运算，使其成为某个常用函数的麦克劳林......
2023-10-27
-
解析函数导数的几何意义-复变函数及其应用详细阅读
设w = f(z)在区域D内解析,z0 ∈D,且f′(z0) 0,C为z平面内通过点z0的一条有向光滑曲线（图6.3(a)):z0 =z(t0),且z′(t0)0,在映射w =f(z)下,C的象曲线Γ(图6.3(b)) 为：w(t0)=w0,Γ的正向为参数t增大的方向.根据复合函数的求导法则,有因此,在Γ上点w0处的切线存在,并且切线的正向与u 轴正向之间的夹角是即这表明,曲线Γ在w0 = f(z......
2023-10-30
-
复变函数导数及应用-复变函数及其应用详细阅读
复变函数导数的定义在形式上与一元实变函数一致.定义1 设函数w = f(z)在点z0的某个邻域内有定义,且z0+△z是该邻域中的点,如果极限存在,我们称f(z)在点z0处可导(或可微),并称此极限值为f(z)在z0 点处的导数,记作若函数w = f(z)在点z0可导,导数为f′(z0),那么对于任意给定的ε ＞0,相应地存在δ(ε)＞0,使得当0 ＜|△z|＜δ时,有若函数w =f(z)在区域D内......
2023-10-30
相关推荐