设α1,α2,··· ,αn,··· 为一个复数列,其通项为α=an+ibn,可简记该复数列为{αn}.定义1 设{αn}为一个复数列且α = a+ib为复常数.若对任意正数ε都存在对应的正整数N,使当n >N时恒有|αn-α| <ε,则称该复数列收敛且其极限为α,记为这时也称复数列{αn}收敛于α,如果不存在任何有限复常数α使得复数列{αn} 收敛于α,则称复数列{αn}是发散的.由复数列{αn......
2023-10-30
设{αn}={an+ibn}(n=1,2,···) 为一复数列,表达式
称为无穷级数,其前n项的和
称为级数的部分和.
若该部分和数列收敛,其极限为S,则称上述复数项级数收敛,且称S 为该级数的和,记为
若部分和数列{Sn}发散,则称级数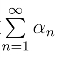 发散.
发散.
定理4 级数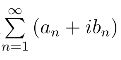 收敛的充要条件是其实部级数
收敛的充要条件是其实部级数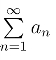 和虚部级数
和虚部级数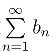 都收敛.
都收敛.
证明 因
其中σn =a1+a2+···+an,τn =b1+b2+···+bn 分别为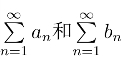 的部分和.由定理2,Sn 有极限存在的充要条件是σn 和τn 的极限存在,即级数
的部分和.由定理2,Sn 有极限存在的充要条件是σn 和τn 的极限存在,即级数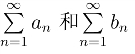 都收敛.
都收敛.
定理4将复数项级数的审敛问题转化为实数项级数的审敛问题,而由实数项级数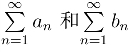 收敛的必要条件
收敛的必要条件
立即可得![]()
定理5 复数项级数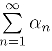 收敛的必要条件是
收敛的必要条件是![]() (www.chuimin.cn)
(www.chuimin.cn)
如果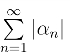 收敛,那么称级数
收敛,那么称级数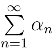 为绝对收敛.非绝对收敛的收敛级数称为条件收敛级数.
为绝对收敛.非绝对收敛的收敛级数称为条件收敛级数.
定理6 若![]() 也收敛.
也收敛.
证明 由于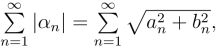 而
而
根据实数项级数的比较准则,可知级数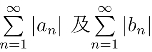 都收敛,因而
都收敛,因而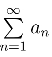 和
和![]() 也都收敛.由定理2,可知
也都收敛.由定理2,可知![]() 是收敛的.由定理6知,若级数绝对收敛,则它本身一定收敛,但反之不真.
是收敛的.由定理6知,若级数绝对收敛,则它本身一定收敛,但反之不真.
例2 判别下列级数的收敛性,若级数收敛,指出是绝对收敛还是条件收敛.
解 (1)因|αn|≥1不趋向于零,由定理5,该级数发散.
(2)因![]() 由正项级数的比值审敛法知
由正项级数的比值审敛法知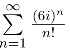 收敛,故原级数收敛,且为绝对收敛.
收敛,故原级数收敛,且为绝对收敛.
(3)其实部级数为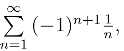 虚部级数为
虚部级数为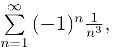 由交错级数判别法可知它们都收敛,于是由定理3,得所给原级数收敛.
由交错级数判别法可知它们都收敛,于是由定理3,得所给原级数收敛.
又由于![]() 由调和级数的发散性和正项级数比较判别法得,所给原级数非绝对收敛,因而条件收敛.
由调和级数的发散性和正项级数比较判别法得,所给原级数非绝对收敛,因而条件收敛.
有关复变函数及其应用的文章

设α1,α2,··· ,αn,··· 为一个复数列,其通项为α=an+ibn,可简记该复数列为{αn}.定义1 设{αn}为一个复数列且α = a+ib为复常数.若对任意正数ε都存在对应的正整数N,使当n >N时恒有|αn-α| <ε,则称该复数列收敛且其极限为α,记为这时也称复数列{αn}收敛于α,如果不存在任何有限复常数α使得复数列{αn} 收敛于α,则称复数列{αn}是发散的.由复数列{αn......
2023-10-30

我们通常称z = x+iy为复数z的代数形式.除此之外,复数z还有多种表示形式,下面介绍复数的几种表示方法.由于复数z =x+iy由一个有序实数对(x,y)唯一确定,在取定平面直角坐标系xOy时,实数对(x,y)可视为平面直角坐标系中的两个坐标组成的序对,这就建立了复数z与平面上的点的一一对应关系,于是对于任意一个复数z =x+iy,都对应于平面上的一点P(x,y),故可用实数对形式(x,y)表示......
2023-10-30

复变函数导数的定义在形式上与一元实变函数一致.定义1 设函数w = f(z)在点z0的某个邻域内有定义,且z0+△z是该邻域中的点,如果极限存在,我们称f(z)在点z0处可导(或可微),并称此极限值为f(z)在z0 点处的导数,记作若函数w = f(z)在点z0可导,导数为f′(z0),那么对于任意给定的ε >0,相应地存在δ(ε)>0,使得当0 <|△z|<δ时,有若函数w =f(z)在区域D内......
2023-10-30

对于收敛圆的圆心相同的两个复数项幂级数,它们的四则运算可以像实数项幂级数那样来进行,要根据其系数来确定.对于和、差、积所得幂级数在其公共收敛圆内显然收敛,其收敛半径不会小于所给级数的收敛半径最小的一个.如对乘积运算若上式左端两个幂级数的收敛半径分别为R1和R2,则其积的幂级数收敛半径R >min{R1,R2}.为了说明两个幂级数经过运算后所得的幂级数的收敛半径确实可以大于R1 和R2 中较小的一个......
2023-10-30

幂函数w =zn(n ≥2为自然数)在z平面上处处可导,且除去原点外导数不为零,因此,在z平面上除去原点外是处处保角的.下面讨论w = zn在原点的性质.若令z = reiθ,w = ρeiφ,则由ρeiφ =rnelnθ,得由此可知,在w = zn映射下,z平面上的圆周|z| = r映射成w 平面上的圆周|w|=rn,射线arg z =θ0 映射成射线arg w =φ=nθ0,正实轴θ =0映射......
2023-10-30

如果是极点,指出它的级.解 令ζ = 则由于g(ζ)在ζ = 0解析且g 0,所以ζ = 0是的简单极点,因此z = ∞是f 的简单极点.......
2023-10-30

在圆环域R1 <|z-z0|<R2内处处解析的函数f(z)可以展开成z-z0的正、负幂项都有的级数,称为f(z)的洛朗(Laurent) 级数.定理1(洛朗级数展开定理) 设R1 <|z - z0| <R2 为环域D,函数f(z)在D内解析,则对D 内任意点z有其中C为在该环域内任意一条围绕点z0的正向简单闭路.证明对任意z ∈D,在D内分别作正向圆周C1 和C2,其中C1为|ζ-z0|=r1,C......
2023-10-30

设z1 =r1eiθ1,z2 =r2eiθ2,··· ,zn =rneiθn是n个非零复数,用数学归纳法可以得到这n个复数的乘积为特别地,当这n个复数相同时,我们把n个相同的复数z的乘积称为z的n次幂,记作zn.设z =reiθ,则zn =rneinθ =rn(cos nθ+i sin nθ).当r =1时,即z =cos θ+i sin θ,有(cos θ+i sin θ)n =cos nθ+i......
2023-10-30
相关推荐