解析函数是指在某个区域内可导的函数,它在理论和实际问题中应用广泛,具体定义如下:定义2 若函数f(z)在点z0的某个邻域内(包含点z0)处处可导,我们称f(z)在点z0处解析,也称它在z0全纯或正则,并称z0 是f(z) 的解析点,若函数f(z)在点z0处不解析,则称点z0 是f(z)的奇点; 若函数f(z)在区域D内的每一点都解析,则称函数f(z)在区域D内解析,或称f(z)是区域D内的解析函数......
2025-09-30
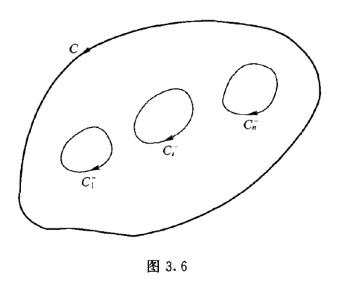
所谓复合闭路是指一种特殊的有界多连通域D的边界曲线Γ,它由几条简单闭曲线组成,可简记为Γ=![]() 其中简单闭路C取正向; 简单闭路
其中简单闭路C取正向; 简单闭路![]() 取负向,它们都在C 的内部且互不相交又互不包含(图3.6).上述Γ 的方向称为多连域D的边界曲线的正向.
取负向,它们都在C 的内部且互不相交又互不包含(图3.6).上述Γ 的方向称为多连域D的边界曲线的正向.
定理3(复合闭路定理) 设D是以复闭路Γ = ![]() 为边界的多连通域.若函数f(z) 在D内及其边界Γ上解析,则f(z)沿Γ的积分为零.这时有
为边界的多连通域.若函数f(z) 在D内及其边界Γ上解析,则f(z)沿Γ的积分为零.这时有
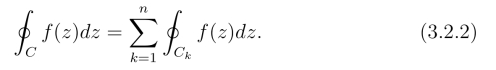
证明 只须证n = 2的情形.在区域D内作割线段把D分成区域D1和D2(如图3.7).设D1和D2的边界正向曲线分别为Γ1和Γ2.由定理所给条件,f(z)在简单闭路Γ1和Γ2上及其内部解析,于是由定理1得

由于Γ1和Γ2在上述割线段上重合且反向,Γ1和Γ2的其余部分组成了D的边界Γ且与Γ同向,因此上式可化简为

可得所证等式(3.2.2)成立.
定理3说明,在区域内的一个解析函数沿闭曲线的积分,不因闭曲线在区域内作连续变形而改变它的值,只要在变形过程中曲线不经过函数f(z)不解析的点.这一性质,称为闭路变形原理.
 (https://www.chuimin.cn)
(https://www.chuimin.cn)
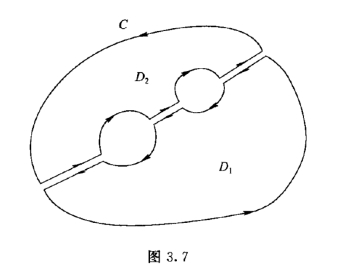
例如,从本章3.1的例1知:当C为z0为中心的正向圆周时,![]() 所以,根据闭路变形原理,对于包含z0的任何一条正向简单闭曲线Γ(图3.8)都有:
所以,根据闭路变形原理,对于包含z0的任何一条正向简单闭曲线Γ(图3.8)都有:![]()
对于多连通区域,若一个函数在区域的边界和内部解析,根据闭路变形原理,可以把外边界上的积分转化为在所有边界上的积分.
例2 设C为正向圆周|z|=10,计算积分

解 由于![]() 于是得
于是得
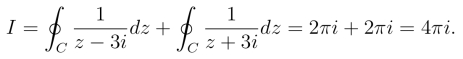
例3 计算![]() 的值,Γ为包含圆周|z|=2在内的任何正向简单闭曲线.
的值,Γ为包含圆周|z|=2在内的任何正向简单闭曲线.
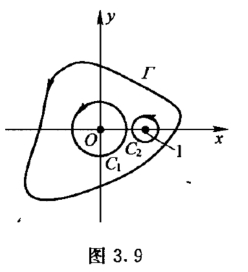
解 函数![]() 在复平面内除z =0和z =1两个奇点外处处解析.由于Γ是包含圆周|z| = 1在内的任何正向简单闭曲线,因此它包含这两个奇点.在Γ内作两个互不包含也互不相交的正向圆周C1 和C2,C1只包含奇点z =0,C2只包含奇点z =1(图3.9),那么根据复合闭路定理得
在复平面内除z =0和z =1两个奇点外处处解析.由于Γ是包含圆周|z| = 1在内的任何正向简单闭曲线,因此它包含这两个奇点.在Γ内作两个互不包含也互不相交的正向圆周C1 和C2,C1只包含奇点z =0,C2只包含奇点z =1(图3.9),那么根据复合闭路定理得
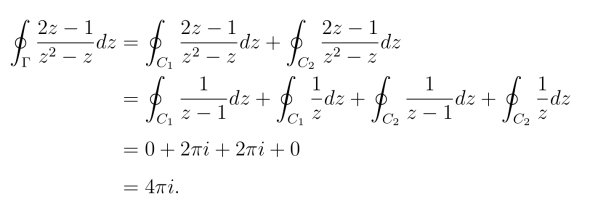
从这个例子我们看到:借助于复合闭路定理,有些比较复杂的函数的积分可以化为比较简单的函数的积分.这是计算积分常用的一种方法.
相关文章

解析函数是指在某个区域内可导的函数,它在理论和实际问题中应用广泛,具体定义如下:定义2 若函数f(z)在点z0的某个邻域内(包含点z0)处处可导,我们称f(z)在点z0处解析,也称它在z0全纯或正则,并称z0 是f(z) 的解析点,若函数f(z)在点z0处不解析,则称点z0 是f(z)的奇点; 若函数f(z)在区域D内的每一点都解析,则称函数f(z)在区域D内解析,或称f(z)是区域D内的解析函数......
2025-09-30

定义3 设α是任意一个复数,定义幂函数为w =zα =eαLnz(z 0).在α为正实数时,对z =0的情况进行规定:zα =0.幂函数是指数函数与对数函数的复合函数,根据对数函数的定义,有w =zα =eαLnz =eα(ln z+2kπi) =eα ln z·e2αkπi,(k为整数)由于Lnz = ln z+2kπi是多值的,所以w = zα也是多值的,且所取的不同数值的个数等于e2αkπi......
2025-09-30

设z1 =r1eiθ1,z2 =r2eiθ2,··· ,zn =rneiθn是n个非零复数,用数学归纳法可以得到这n个复数的乘积为特别地,当这n个复数相同时,我们把n个相同的复数z的乘积称为z的n次幂,记作zn.设z =reiθ,则zn =rneinθ =rn(cos nθ+i sin nθ).当r =1时,即z =cos θ+i sin θ,有(cos θ+i sin θ)n =cos nθ+i......
2025-09-30

定理1 如果函数u=φ(t)及v=ψ(t)都在点t可导,函数z=f(u,v)在对应点(u,v)处具有连续偏导数,则复合函数z=f[φ(t),ψ(t)]在点t处可导,且其导数可用下列公式计算定理1可推广到复合函数的中间变量多于两个的情形.例如,设z=f(u,v,ω),u=φ(t),v=ψ(t),w=ω(t)复合而得复合函数则在与定理相类似的条件下,复合函数在点t可导,且其导数可用下列公式计算式(8.......
2025-09-30

设C为平面上给定的一条光滑(或逐段光滑)曲线,则沿曲线C有两个方向,若选定其中的一个方向作为正方向,则称曲线C为有向曲线.设曲线C有两个端点A与B,若把从A到B的方向作为曲线C的正方向,则从B到A的方向就是C的负方向,记作C-.对于简单闭曲线,其正方向是指曲线上的点P沿此方向在该曲线前进时,邻近P点的曲线内部始终位于P点的左方,与之相反的方向就是曲线的负方向,而当曲线C为圆周时,逆时针方向就是曲线......
2025-09-30

【主要内容】计算函数的导数的基础是求导基本公式和四则运算法则.求导基本公式:(1)C′=0(C是常数),(2)(xμ)′=μxμ-1,(3)(ax)′=axlna(常数a>0但a≠1),特别地,(ex)′=ex,(4),特别地,,(5)(sinx)′=cosx, (6)(cosx)′=-sinx,(7)(tanx)′=sec2x, (8)(cotx)′=-csc2x,(9)(secx)′=secx......
2025-09-30

|z-1|<|z+3|; -1 <arg z <-1+π;0 <arg(z-1)<,且Rez <3; 2 ≤|z|≤3;Imz ≤2; |3z+i|<3;|z+2|+|z-2|≤6; 1 <|z-i|<3.解 是无界单连通区域; 是无界单连通区域; 是有界的单连通域; 有界的多连通闭区域; 是无界单连通闭区域; 有界单连通区域; 是有界闭区域,不是区域; 是有界多连通区域.......
2025-09-30

复变函数和实变函数类似,同样可以讨论函数的极限和连续性,且形式基本上与实变函数一致.现在介绍复变函数的极限概念.定义3 设函数w = f(z)在点z0的去心邻域:0 <|z - z0| <ρ内有定义.如果存在一个复常数A,使得对于任意给定的ε >0,总存在一个实数δ >0(δ <ρ),当0 <|z-z0|<δ 时,有|f(z)-A|<ε,我们称A为f(z)当z趋于z0时的极限,记为复变函数极限的几......
2025-09-30
相关推荐