复功率的单位仍用。 如图4.15所示，把一个线圈接到f=50Hz的正弦电源上，分别用电压表、电流表、功率表测得电压U=50V、电流I=1A、功率P=30W，试求R、L之值，并求线圈吸收的复功率。解：根据三个电表的读数，可先求线圈阻抗图4.15[例4.8]电路图功率表的读数为线圈吸收的有功功率，则图4.15[例4.8]电路图功率表的读数为线圈吸收的有功功率，则还可以用另外一种方法，即还可以用另外一种方法，即......
2025-09-29
复积分计算公式及条件
【摘要】：下面讨论积分式(3.1.1)在什么条件下存在.函数f(z)=u(x,y)+iv(x,y)在D内处处连续,则u(x,y)及v(x,y)均为D内的连续函数.设ζk =ξk+iηk,由于因此由于u,v都是连续函数,根据线积分的存在定理可知,当弧段长度的最大值趋于零时,不论对C的分法如何,点(ξk,ηk) 的取法如何,上式右端的两个和式的极限都是存在的.因此有为便于记忆,公式(3.1.2)在形式上可以看作
下面讨论积分式(3.1.1)在什么条件下存在.
函数f(z)=u(x,y)+iv(x,y)在D内处处连续,则u(x,y)及v(x,y)均为D内的连续函数.设ζk =ξk+iηk,由于
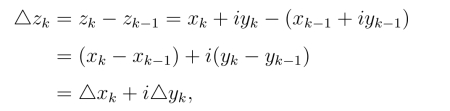
因此
由于u,v都是连续函数,根据线积分的存在定理可知,当弧段长度的最大值趋于零时,不论对C的分法如何,点(ξk,ηk) 的取法如何,上式右端的两个和式的极限都是存在的.因此有
为便于记忆,公式(3.1.2)在形式上可以看作f(z) = u+iv与dz = dx+idy相乘后求积分得到,即
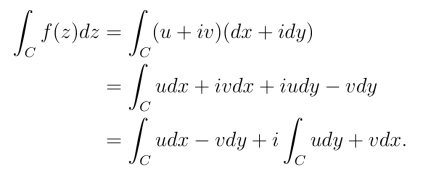
我们有下面结论:
定理(复积分存在的充分条件) 若C为光滑或逐段光滑的有向曲线段,f(z) 在C 上处处连续,则f(z)沿C 可积.
利用公式(3.1.2)可以计算函数f(z)沿曲线C的积分,可是需要计算两个二元实函数对坐标的曲线积分,通常很麻烦.下面对曲线C 为光滑曲线的情形,将该公式化为更简单的形式.
若C为有向光滑曲线,其参数方程为z =z(t)=x(t)+iy(t)(α ≤t ≤β),则z′(t)=x′(t)+iy′(t) 在区间[α,β]上连续且不等于零.
根据线积分的计算方法,有
上式右端可以写成
(https://www.chuimin.cn)
所以
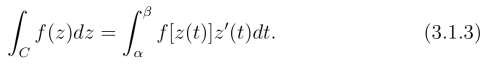
用公式(3.1.3)来计算复积分比较简便,该式可看作一般复积分的计算公式.
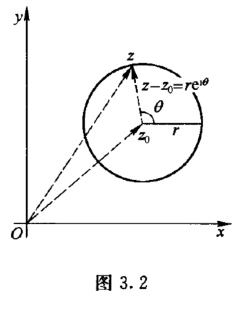
例1 设C为正向圆周|z-z0|=r(r ＞0),n为正整数,试证:
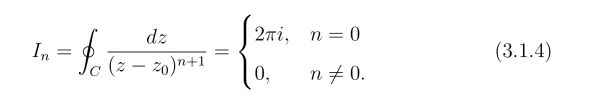
证明 C的方程写作z =z0+reiθ,0 ≤θ ＜2π(图3.2),所以
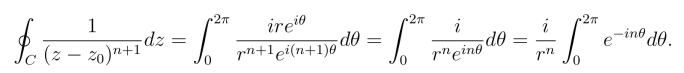
当n=0时得
当n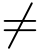
0时得
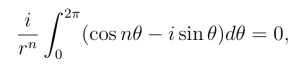
因此
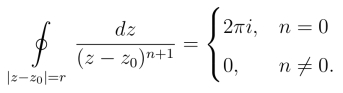
式(3.1.4)以后经常用到,可作为积分公式来使用,它的特点是积分值与积分路线圆周的中心和半径无关.
相关文章
- 详细阅读
-
不定积分的换元积分法详细阅读
【主要内容】1.不定积分的概念函数f（x）在区间I上的原函数全体F（x）+C（其中，F（x）是f（x）的一个原函数，即F′（x）=f（x），C是任意常数），称为f（x）的不定积分，记为∫f（x）dx.不定积分的计算主要依靠不定积分的基本公式、基本性质及基本运算方法.基本公式（1），（2），（3），（4），（5），（6），（7），（8），（9），特别地，，（10），（11），（12），此外，还有（1......
2025-09-30
-
复变函数应用：复球面与扩展复平面详细阅读
在第一节中我们知道,复数与平面内的点或向量建立了一一对应关系,所以我们对复数、平面内的点和向量不加区别.除此之外,复数也可与球面上的点一一对应,并用球面上的点来表示,具体做法如下：取一个球面,使之与复平面z相切于原点,球面上的一点S与原点重合,如(图1-5).通过点S作一条垂直于复平面的直线与球面交于另一点N,我们称N为北极,S为南极.对于复平面内任何一点z,现在用直线段将点z与北极N连接起来,那......
2025-09-30
-
反常积分收敛性及计算方法详细阅读
【主要内容】1.无穷限反常积分（1）无穷限反常积分定义设函数f（x）在[a，+∞）上连续.如果极限存在，则称这个极限值为f（x）在[a，+∞）上的反常积分，记为，此时称反常积分收敛；如果极限不存在，则称反常积分发散.设函数f（x）在（-∞，b]上连续.如果极限存在，则称这个极限值为f（x）在（-∞，b]上的反常积分，记为，此时称反常积分收敛；如果极限不存在，则称反常积分发散.设函数f（x）在（-∞......
2025-09-30
-
干部培养问题及条件分析详细阅读
在学校训练到出校后的训练，是从训练干部慢慢走到培养干部。一株树要长大，要开花结果，也要有空气、水分和肥料；因此干部的培养也要有许多条件：一要爱护干部——这可以说是关于我们自己的，也可以说是关于你们自己的。四要组织干部——我们不能让干部像散沙一样，我们要把他们加以组织。关于这问题，主席和本人都很看重。......
2025-09-29
-
积分中值定理的应用及解析详细阅读
【主要内容】1.积分中值定理设函数f（x）在[a，b]上连续，则存在ξ∈[a，b]，使得注 （ⅰ）当上述的f（x）是单调函数时，中值ξ∈（a，b）.（ⅱ）积分中值定理具有以下的推广形式：设函数f（x）在[a，b]上连续，函数g（x）在[a，b]上可积且不变号，则存在ξ∈[a，b]，使得2.积分中值定理的应用积分中值定理主要用于把抽象函数f（x）的定积分转换成f（x）在[a，b]上某点η处的值与（b......
2025-09-30
-
区域概况及计算条件分析详细阅读
阿海电站附近气温逐月平均值差别不大，全年平均气温在12.7℃左右。由于入流位置缺乏水温实测资料，采用蓄水前阿海测站和上游石鼓测站的水温进行插值作为阿海水库的入流水温。由于阿海电站上游地势较高，入流水温季节变化明显。根据阿海水库深泓线蜿蜒曲折和河道长宽比悬殊的特点，在平面上采用曲线正交四边形网格剖分计算区域。考虑到阿海水库河宽较小，沿河宽方向水温变化较小，在河宽方向划分为5个网格。......
2025-09-29
-
大气复氧机理及双膜理论简析详细阅读
对于大坝泄流和近岸海域，受风、潮汐、波浪等的影响，水体几乎无法保持静止状态，紊动复氧是大气复氧的重要过程。因此，大气复氧一般指紊动水体大气复氧。双膜理论是应用较多的一种理论模型。双膜理论把复杂问题大大简化，对低流速情况相当符合。在高紊动水体，由于自由表面产生严重变形，两相界面被漩涡贯穿，双膜理论中刚性自由表面及层流膜的假设不再成立，因此该理论不适用于高紊动水体。......
2025-09-29
相关推荐