定义1 由扩充复平面上4个有序的相异点z1,z2,z3,z4构成的比式称为它们的交比,记作(z1,z2,z3,z4).若4点中有一个为∞,应将包含此点的分子或分母用1代替,例如z1 =∞,则对于扩充z平面上4个有序的相异点z1,z2,z3,z4经整线性映射w =az+b,得到扩充w平面上的4个点w1,w2,w3,w4,由于即整线性映射具有交比不变性.同样可验证w =具有交比不变性.综上可知,分式线......
2023-10-30
复变指数函数的定义及性质
【摘要】：从上节例2可知,f(z)=ex(cos y+i sin y)在整个复平面上解析,且f′(z)=f(z).容易验证f(z1+z2) =f(z1)+f(z2),据此我们给出复变指数函数的定义.定义1 对任意的复数z =x+iy,定义指数函数为w =ex(cos y+i sin y),记作ez.显然,|ez|=ex ＞0,而Arg(ez)=y+2kπ(k为整数),从而ez 0.当z 取实数,即y = 0
从上节例2可知,f(z)=ex(cos y+i sin y)在整个复平面上解析,且f′(z)=f(z).容易验证f(z1+z2) =f(z1)+f(z2),据此我们给出复变指数函数的定义.
定义1 对任意的复数z =x+iy,定义指数函数为
w =ex(cos y+i sin y),
记作ez.
显然,|ez|=ex ＞0,而Arg(ez)=y+2kπ(k为整数),从而ez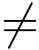 
0.当z 取实数,即y = 0,z = x时,ez = ex,此时它与实变量指数函数ex 一致,可见复指数函数是实指数函数的推广.当z取纯虚数,即x = 0,z = iy 时,得到欧拉(Euler)公式
ez =eiy =cos y+i sin y.
由定义,容易验证指数函数ez具有下列性质：
(1) 复变量指数函数ez在整个复平面内都有定义,且在整个复平面内解析,有
(2) ez满足加法、减法定理,对于任意的z1,z2,有
事实上,设z1 =x1+iy1,z2 =x2+iy2,则(www.chuimin.cn)
同理可证.但(ez1)z2 =ez1z2一般不成立.
(3) 由加法定理,可推出ez的周期性.对任意整数k,都有
因为
一般地,对任意整数k,都有
2πi是ez的周期且模最小,我们称2πi是ez的基本周期.因此,我们常说ez是以2πi为周期的周期函数.
(4)
不存在.
例1 设z =x+iy,求
解 因为
所以其模|ez|=ex,实部Re(ez)=ex cos y.
有关复变函数及其应用的文章
- 详细阅读
-
复变函数的定义及应用详细阅读
复变函数的定义在形式上与一元实函数一样,只是将自变量和因变量都推广到了复数域.定义1 设D为复平面上的非空集合[1],若有一个确定的法则存在,按照这一法则,对于D 内的每一个复数z =x+iy,都有确定的复数w =u+iv 与之对应,我们称复变数w是z的复变函数,记为w =f(z).其中z称为自变量,w为因变量,集合D称为w = f(z)的定义域,与D 中所有复数z对应的w值的集合G 称为w =f......
2023-10-30
-
拉氏变换性质|复变函数及应用详细阅读
这一节将介绍拉氏变换的几个基本性质,它们在拉氏变换的实际应用中都是很有用的.为了叙述方便,假定在这些性质中,凡是要取拉氏变换的函数都满足拉氏变换存在定理中的条件,并且把这些函数的增长指数统一地设为c.在证明这些性质时,不再重复这些条件.1.线性性质设α,β为常数,且则有或2.相似性质设a ＞0,若L[f(t)]=F (p),则类似有以上两条性质的证明与傅氏变换相应的性质的证明是一样的.3.微分性质......
2023-10-30
-
幂函数的规定及性质-复变函数及其应用详细阅读
定义3 设α是任意一个复数,定义幂函数为w =zα =eαLnz(z 0).在α为正实数时,对z =0的情况进行规定：zα =0.幂函数是指数函数与对数函数的复合函数,根据对数函数的定义,有w =zα =eαLnz =eα(ln z+2kπi) =eα ln z·e2αkπi,(k为整数)由于Lnz = ln z+2kπi是多值的,所以w = zα也是多值的,且所取的不同数值的个数等于e2αkπi......
2023-10-30
-
矩阵秩的定义及性质分析详细阅读
【主要内容】1.矩阵秩的定义设A是m×n矩阵，则称A的不为零的子行列式（简称子式）的最高阶数为A的秩，记为r（A），其中，A的k（k≤min{m，n}）阶子式是指A的k行k列交叉位置的元素构成的k阶行列式.零矩阵的秩定义为0.2.矩阵秩的性质（1）设A是m×n矩阵，则0≤r（A）≤min{m，n}.（2）设A是m×n矩阵，k是常数，则（3）初等变换不改变矩阵的秩，即等价矩阵的秩相等.（4）设A，B......
2023-10-27
-
矩阵相似定义及性质概述详细阅读
1.矩阵相似的定义设A，B都是n阶矩阵.如果存在n阶可逆矩阵P，使得B=P-1AP，则称矩阵A与B相似，也称A与B为相似矩阵，记为A～B.2.矩阵相似的性质设A，B，C都是n阶矩阵，则有以下性质：A～A.如果A～B，则B～A.如果A～B，B～C，则A～C.如果A～B，则AT～BT，Am～Bm，λA～λB，φ～φ（其中，φ（λ）=a0+a1λ+…......
2023-10-27
-
高等代数：实数域上的内积定义及性质详细阅读
定义6.1 在实数域R上的线性空间V中，定义一个二元函数V×V→R，称为向量α，β∈V的内积，记作<α，β>，如果下面几个条件同时成立：（1）<α，β>=<β，α>，对任意向量α，β∈V成立；（2）
2023-11-22
-
复积分在复变函数中的定义详细阅读
设C为平面上给定的一条光滑(或逐段光滑)曲线,则沿曲线C有两个方向,若选定其中的一个方向作为正方向,则称曲线C为有向曲线.设曲线C有两个端点A与B,若把从A到B的方向作为曲线C的正方向,则从B到A的方向就是C的负方向,记作C-.对于简单闭曲线,其正方向是指曲线上的点P沿此方向在该曲线前进时,邻近P点的曲线内部始终位于P点的左方,与之相反的方向就是曲线的负方向，而当曲线C为圆周时,逆时针方向就是曲线......
2023-10-30
相关推荐