设C为平面上给定的一条光滑(或逐段光滑)曲线,则沿曲线C有两个方向,若选定其中的一个方向作为正方向,则称曲线C为有向曲线.设曲线C有两个端点A与B,若把从A到B的方向作为曲线C的正方向,则从B到A的方向就是C的负方向,记作C-.对于简单闭曲线,其正方向是指曲线上的点P沿此方向在该曲线前进时,邻近P点的曲线内部始终位于P点的左方,与之相反的方向就是曲线的负方向，而当曲线C为圆周时,逆时针方向就是曲线......
2023-10-30
复变函数应用：复球面与扩展复平面
【摘要】：在第一节中我们知道,复数与平面内的点或向量建立了一一对应关系,所以我们对复数、平面内的点和向量不加区别.除此之外,复数也可与球面上的点一一对应,并用球面上的点来表示,具体做法如下：取一个球面,使之与复平面z相切于原点,球面上的一点S与原点重合,如(图1-5).通过点S作一条垂直于复平面的直线与球面交于另一点N,我们称N为北极,S为南极.对于复平面内任何一点z,现在用直线段将点z与北极N连接起来,那
在第一节中我们知道,复数与平面内的点或向量建立了一一对应关系,所以我们对复数、平面内的点和向量不加区别.除此之外,复数也可与球面上的点一一对应,并用球面上的点来表示,具体做法如下：
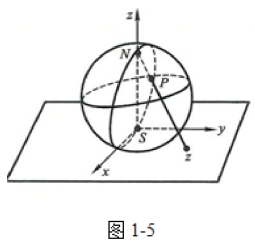
取一个球面,使之与复平面z相切于原点,球面上的一点S与原点重合,如(图1-5).通过点S作一条垂直于复平面的直线与球面交于另一点N,我们称N为北极,S为南极.
对于复平面内任何一点z,现在用直线段将点z与北极N连接起来,那么该直线段一定与球面相交于异于N的一点P.反过来,对于球面上任何异于N的点P,用一直线段把P与N连接起来,这条直线段的延长线就与复平面相交于一点z.这就说明,球面上的点,除北极N外,与复平面内的点之间存在着一一对应的关系.于是复球面上的点,除北极N外也与复数一一对应.因此我们可以用这个球面上的点表示复数.
但是,复平面内没有一个点与球面上的北极N对应.从(图1-5)可以看到,当点z无限远离原点时,或者说,当z 的模|z|无限变大时,点P就无限接近于N.为了使复平面与球面上的点无一例外地都能一一对应起来,我们规定：复平面上有唯一的“无穷远点”,它与球面上北极N相对应.相应地,我们又规定:复数中有唯一的“无穷大”与复平面上的“无穷远点”相对应，并把它记作∞.因而球面上的北极N就是复数无穷大∞的几何表示.这样一来,球面上的每一点,就有唯一的复数与它对应,这样的球面称为复球面.
我们把包括无穷远点在内的复平面称为扩充复平面或黎曼球面,记作
.不包括无穷远点在内的复平面称为有限复平面,或者就称复平面,用C表示.在本教材中,如无特殊声明,复平面都指有限复平面,复数z都指有限复数.对于复数∞来说,实部、虚部与辐角的概念均无意义,但它的模规定为正无穷大,即|∞|=+∞.对于其它的每一个复数,则有|z|＜+∞.
“无穷远点”作为一个新的数引入复数域,我们对它的运算作如下规定：(www.chuimin.cn)
(1)当z 
∞时,∞±z =∞,z±∞=∞;
(2)当z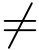 
0 时,∞·z =∞,z·∞=∞;
(3)当z 
∞时,
(4)当z 
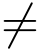0时,
此外,下列其它运算是没有确定意义的：
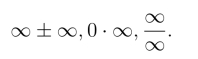
有关复变函数及其应用的文章
- 详细阅读
-
复积分基本性质详解-复变函数及其应用详细阅读
从复积分的定义,可以推得复积分具有下列基本性质,它们与实变函数中定积分的性质类似.若复变函数f(z)和g(z)沿其积分路径C可积,则有1° f(z)±g(z)沿C可积,且有2° 对任意复数A=a+ib,函数Af(z)沿C可积,有3° f(z)沿C的反向曲线C-可积,且有4° (复积分对积分路径的可加性)若函数f(z)沿曲线Ck(k =1,2,··· ,n)可积,且C 由Ck依次连接而成,则f(z)......
2023-10-30
-
复变函数及其应用：整线性映射在扩充复平面具有详细阅读
在第1章中我们已经提出,如果把直线看成是半径为无穷大的圆周,则在扩充复平面具有保圆性.下面说明整线性映射在扩充复平面也具有保圆性.令a=|a|ela,则整线性映射w =az+b 可分解成对于w = z +b由复向量的加法,对复平面上任一点z,点w = z +b是点z沿向量b的方向平移了|b|的距离.因此它的作用是把复平面上的任何图形沿复向量b的方向平移了距离|b|,称该映射为平移.对于w =ela......
2023-10-30
-
复平面曲线方程及其应用详细阅读
实平面上曲线有直角坐标方程和参数方程两种形式，复平面上的曲线也有直角坐标方程和参数方程两种复数形式.(1)直角坐标方程设z =x+iy,若平面曲线C的直角坐标方程为F(x,y)=0,由可得平面曲线C在复平面上复数形式的方程例1 把直线方程3x+2y =1化为复数形式.解 将代入方程,得为所给直线方程的复数形式.(2)参数方程令z =x+iy,若平面曲线C的参数方程为x=x(t),y =y(t)(α......
2023-10-30
-
复变函数与应用-复变函数及其应用详细阅读
幂函数w =zn(n ≥2为自然数)在z平面上处处可导,且除去原点外导数不为零,因此,在z平面上除去原点外是处处保角的.下面讨论w = zn在原点的性质.若令z = reiθ,w = ρeiφ,则由ρeiφ =rnelnθ,得由此可知,在w = zn映射下,z平面上的圆周|z| = r映射成w 平面上的圆周|w|=rn,射线arg z =θ0 映射成射线arg w =φ=nθ0,正实轴θ =0映射......
2023-10-30
-
复变函数及应用：平面点集、区域详细阅读
|z-1|＜|z+3|; -1 ＜arg z ＜-1+π;0 ＜arg(z-1)＜,且Rez ＜3; 2 ≤|z|≤3;Imz ≤2; |3z+i|＜3;|z+2|+|z-2|≤6; 1 ＜|z-i|＜3.解 是无界单连通区域； 是无界单连通区域； 是有界的单连通域； 有界的多连通闭区域； 是无界单连通闭区域； 有界单连通区域； 是有界闭区域,不是区域； 是有界多连通区域.......
2023-10-30
-
复变函数导数及应用-复变函数及其应用详细阅读
复变函数导数的定义在形式上与一元实变函数一致.定义1 设函数w = f(z)在点z0的某个邻域内有定义,且z0+△z是该邻域中的点,如果极限存在,我们称f(z)在点z0处可导(或可微),并称此极限值为f(z)在z0 点处的导数,记作若函数w = f(z)在点z0可导,导数为f′(z0),那么对于任意给定的ε ＞0,相应地存在δ(ε)＞0,使得当0 ＜|△z|＜δ时,有若函数w =f(z)在区域D内......
2023-10-30
-
复变函数函数性态-复变函数及其应用详细阅读
如果是极点,指出它的级.解 令ζ = 则由于g(ζ)在ζ = 0解析且g 0,所以ζ = 0是的简单极点,因此z = ∞是f 的简单极点.......
2023-10-30
相关推荐