复变函数导数的定义在形式上与一元实变函数一致.定义1 设函数w = f(z)在点z0的某个邻域内有定义,且z0+△z是该邻域中的点,如果极限存在,我们称f(z)在点z0处可导(或可微),并称此极限值为f(z)在z0 点处的导数,记作若函数w = f(z)在点z0可导,导数为f′(z0),那么对于任意给定的ε ＞0,相应地存在δ(ε)＞0,使得当0 ＜|△z|＜δ时,有若函数w =f(z)在区域D内......
2023-10-30
复变函数及应用：平面点集、区域
【摘要】：|z-1|＜|z+3|; -1 ＜arg z ＜-1+π;0 ＜arg(z-1)＜,且Rez ＜3; 2 ≤|z|≤3;Imz ≤2; |3z+i|＜3;|z+2|+|z-2|≤6; 1 ＜|z-i|＜3.解 是无界单连通区域； 是无界单连通区域； 是有界的单连通域； 有界的多连通闭区域； 是无界单连通闭区域； 有界单连通区域； 是有界闭区域,不是区域； 是有界多连通区域.
上面提到的复平面上的直线、圆周等曲线都是复平面上的点集,以下介绍平面点集的几个基本概念.
(1)邻域
定义3 设z0是复平面上的一点,δ是任意的正数.我们称以z0为中心,δ为半径的圆内部的点集{z||z-z0| ＜δ}为z0的一个δ邻域,记作U(z0;δ).若不强调半径大小时,可简称为z0的邻域,简记为U(z0).称满足不等式0 ＜|z-z0|＜δ 的点集为z0一个的去心邻域,简记为˚U(z0).
(2)点与点集的关系
定义4 设E为平面上的一个点集,z0为E内一点,若存在z0 的邻域U(z0),使得U(z0) ⊂E,我们称z0为E的内点.若存在z0 的邻域U(z0),使得U(z0)∩E = Ø,则称z0为E的外点.若z0不是E的内点,也不是E的外点,则称z0为E的界点或边界点.E的所有边界点组成E的边界,记作∂E.
显然，若z0是E的一个内点,则z0 ∈E,反之则不一定成立; 若z0是E的一个外点,则z0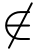 
E,反之,若点z0 /∈E,则z0 必不是E的内点,但z0未必是E的外点,可能为E的边界点,边界点z0可以属于集合E,也可以不属于集合E.
为更好地理解内点、外点、边界点的定义,给出下面一个例子.
例3 设E = {z|z = x+iy,0 ＜x ＜1,0 ≤y ≤1},这是一个包含上下两条边,而不包含左右两条边的正方形.可知满足0 ＜x ＜1,0 ＜y ＜1的点z =x+iy为E 的内点; 正方形的每一条边（无论是否属于E）都是E的界点; 除E 的内点与界点以外的点都是E 的外点.
(3)开集、连通集及区域
定义5 若点集E中的每个点都是它的内点,则称E为开集.
定义6 设E为平面上的一个点集,z0为平面上的任意一点.若对于任意的δ ＞0,点z0 的去心邻域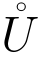
(z0) 内总有E中的点,则我们称z0为E的一个聚点.E的全体聚点组成的集合记为E′.若z0 ∈E,但不是E的聚点,称z0为E的一个孤立点.
定义7 若点集E的聚点的集合包含在E 中,即E′ ⊂E,我们称E为闭集.
例如,单位圆{z||z| ＜1}是开集,带边的单位圆周{z||z| ≤1}是一个闭集,对于后者,单位圆周{z||z|=1}上的点不是它的内点.
在解析函数论中，最常用的集合是区域.
定义8 若点集E的中任意两个点都可以用一条完全属于E的折线连起来,则称E为连通集.
定义9 若点集E是连通开集,则称点集E为区域.我们称区域E连同它的边界一起所构成的点集称为闭区域,记为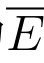
.
区域的边界通常由平面上一条或几条光滑曲线和一些孤立点组成,所围的部分（不包括这些曲线）是区域,所围部分的外部（不包括这些曲线）也是区域.特别是一个圆的内部,或外部都是区域.一条直线把平面分为两部分,其中的每一部分（不包括直线）都是区域.在一个区域内挖掉有限个点剩下的部分是区域.(www.chuimin.cn)
(4)有界集与无界集
定义10 若点集E能完全包含在以原点为中心,以某一个正数R为半径的圆域内,则我们称E 是有界集.不是有界的集合,称为无界集.
例如,单位圆{z||z| ＜1}是有界集,上半平面{z|Imz ＞0}、角域{z|0 ＜arg z ＜φ}等都是无界集.
(5)单连通域与多连通域
一条简单闭曲线C可把整个复平面分为三个互不相交的点集.曲线C是其中一个点集,它们以C为边界,除去曲线C以外,一个是有界区域,称为C的内部,另一个是无界区域,称为C 的外部.环域{z|r ＜|z| ＜R}(r ＞0)从直观上,它的内部有一个”洞”,为了严格刻画这种区域,引入单连通域与多连通域的概念.
定义11 设E是平面上的一个区域,若属于E的任何简单闭曲线的内部总完全属于E,则称E为单连通域,非单连通域称为多连通域.
圆域是单连通域,圆域内挖掉有限个点,余下的部分是多连通域.圆环的内部是多连通域.
例4 说出下列点集是否为区域,是否有界,是否单连通？
(1)|z-1|＜|z+3|; (2)-1 ＜arg z ＜-1+π;
(3)0 ＜arg(z-1)＜
,且Rez ＜3; (4)2 ≤|z|≤3;
(5)Imz ≤2; (6)|3z+i|＜3;
(7)|z+2|+|z-2|≤6; (8)1 ＜|z-i|＜3.
解 (1) 是无界单连通区域； (2) 是无界单连通区域；
(3) 是有界的单连通域； (4) 有界的多连通闭区域；
(5) 是无界单连通闭区域； (6) 有界单连通区域；
(7) 是有界闭区域,不是区域； (8) 是有界多连通区域.
有关复变函数及其应用的文章
- 详细阅读
-
复变函数与应用-复变函数及其应用详细阅读
幂函数w =zn(n ≥2为自然数)在z平面上处处可导,且除去原点外导数不为零,因此,在z平面上除去原点外是处处保角的.下面讨论w = zn在原点的性质.若令z = reiθ,w = ρeiφ,则由ρeiφ =rnelnθ,得由此可知,在w = zn映射下,z平面上的圆周|z| = r映射成w 平面上的圆周|w|=rn,射线arg z =θ0 映射成射线arg w =φ=nθ0,正实轴θ =0映射......
2023-10-30
-
复变函数应用：复球面与扩展复平面详细阅读
在第一节中我们知道,复数与平面内的点或向量建立了一一对应关系,所以我们对复数、平面内的点和向量不加区别.除此之外,复数也可与球面上的点一一对应,并用球面上的点来表示,具体做法如下：取一个球面,使之与复平面z相切于原点,球面上的一点S与原点重合,如(图1-5).通过点S作一条垂直于复平面的直线与球面交于另一点N,我们称N为北极,S为南极.对于复平面内任何一点z,现在用直线段将点z与北极N连接起来,那......
2023-10-30
-
解析函数概念|复变函数及应用详细阅读
解析函数是指在某个区域内可导的函数,它在理论和实际问题中应用广泛,具体定义如下：定义2 若函数f(z)在点z0的某个邻域内(包含点z0)处处可导,我们称f(z)在点z0处解析,也称它在z0全纯或正则,并称z0 是f(z) 的解析点,若函数f(z)在点z0处不解析,则称点z0 是f(z)的奇点; 若函数f(z)在区域D内的每一点都解析,则称函数f(z)在区域D内解析,或称f(z)是区域D内的解析函数......
2023-10-30
-
复变函数的定义及应用详细阅读
复变函数的定义在形式上与一元实函数一样,只是将自变量和因变量都推广到了复数域.定义1 设D为复平面上的非空集合[1],若有一个确定的法则存在,按照这一法则,对于D 内的每一个复数z =x+iy,都有确定的复数w =u+iv 与之对应,我们称复变数w是z的复变函数,记为w =f(z).其中z称为自变量,w为因变量,集合D称为w = f(z)的定义域,与D 中所有复数z对应的w值的集合G 称为w =f......
2023-10-30
-
复变函数函数性态-复变函数及其应用详细阅读
如果是极点,指出它的级.解 令ζ = 则由于g(ζ)在ζ = 0解析且g 0,所以ζ = 0是的简单极点,因此z = ∞是f 的简单极点.......
2023-10-30
-
拉氏变换性质|复变函数及应用详细阅读
这一节将介绍拉氏变换的几个基本性质,它们在拉氏变换的实际应用中都是很有用的.为了叙述方便,假定在这些性质中,凡是要取拉氏变换的函数都满足拉氏变换存在定理中的条件,并且把这些函数的增长指数统一地设为c.在证明这些性质时,不再重复这些条件.1.线性性质设α,β为常数,且则有或2.相似性质设a ＞0,若L[f(t)]=F (p),则类似有以上两条性质的证明与傅氏变换相应的性质的证明是一样的.3.微分性质......
2023-10-30
-
幂函数的规定及性质-复变函数及其应用详细阅读
定义3 设α是任意一个复数,定义幂函数为w =zα =eαLnz(z 0).在α为正实数时,对z =0的情况进行规定：zα =0.幂函数是指数函数与对数函数的复合函数,根据对数函数的定义,有w =zα =eαLnz =eα(ln z+2kπi) =eα ln z·e2αkπi,(k为整数)由于Lnz = ln z+2kπi是多值的,所以w = zα也是多值的,且所取的不同数值的个数等于e2αkπi......
2023-10-30
相关推荐