首页理论教育复平面曲线方程及其应用

复平面曲线方程及其应用

2023-10-30 理论教育版权反馈

【摘要】：实平面上曲线有直角坐标方程和参数方程两种形式，复平面上的曲线也有直角坐标方程和参数方程两种复数形式.(1)直角坐标方程设z =x+iy,若平面曲线C的直角坐标方程为F(x,y)=0,由可得平面曲线C在复平面上复数形式的方程例1 把直线方程3x+2y =1化为复数形式.解将代入方程,得为所给直线方程的复数形式.(2)参数方程令z =x+iy,若平面曲线C的参数方程为x=x(t),y =y(t)(α

实平面上曲线有直角坐标方程和参数方程两种形式，复平面上的曲线也有直角坐标方程和参数方程两种复数形式.

(1)直角坐标方程

设z =x+iy,若平面曲线C的直角坐标方程为

F(x,y)=0,

由可得平面曲线C在复平面上复数形式的方程

例1 把直线方程3x+2y =1化为复数形式.

解将代入方程,得

为所给直线方程的复数形式.

(2)参数方程

令z =x+iy,若平面曲线C的参数方程为

x=x(t),y =y(t)(α ≤t ≤β),

则曲线C的参数方程的复数形式为

z(t)=x(t)+iy(t)或z =z(t)(α ≤t ≤β).

例如,经过z1,z2两点的直线的参数方程为

z =z1+t(z2-z1)(-∞＜t ＜+∞).

由此可知,三点z1,z2,z3共线的充要条件为

或者(www.chuimin.cn)

又如以点(x0,y0)为中心,R为半径的圆的参数方程

x=x0+R cos t,y =y0+R sin t(0 ≤t ≤2π).

所以,该圆的参数方程复数形式为

或

z =z0+R(cos t+i sin t)(0 ≤t ≤2π),其中z0 =x0+iy0.

或

z =z0+Reit(0 ≤t ≤2π).

考虑到|z-z0|表示的是z到z0距离,所以圆的方程也可以写成|z-z0| =R.由此可以看出,有时用复数、复数运算或复数模的几何意义来确定平面曲线C 的方程,或给定一个方程讨论它表示的是什么样的曲线,可能会方便一些.

例2 求下列方程所表示的曲线.

(1)|z+i|=2;(2) |z-z1|+|z-z2|=2a,其中|z1-z2|＜2a;

(3)Im(i+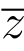 pagenumber_ebook=22,pagenumber_book=13 )=4;(4) z =(1+i)t+z0 (t ＞0).

解(1)将z =x+iy代入方程,可得|x+(y+1)i|=2,即x2+(y+1)2 =4.从几何上不难看出,所求曲线是以-i为中心,2为半径的圆.

(2)由几何意义,曲线是到点z1和点z2距离的和等于2a的点的轨迹,即以z1和z2为焦点,过z1和z2的轴长为2a的椭圆.

(3)设z =x+iy,则i+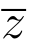 pagenumber_ebook=22,pagenumber_book=13 =x+(1-y)i,所以Im(i+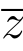)=1-y.从而立

即可得所求曲线的方程为y =-3,这是一条平行于x轴的直线.

(4)将z = x+iy,z0 = x0 +iy0代入方程得x = x0 +t，y = y0 +t.由于t ＞0,所以点z还满足arg(z-z0)=arg[(1+i)t]= 它表示从点z0出发倾角为arg(1+i)=的射线（不包含点z0）.