幂函数w =zn(n ≥2为自然数)在z平面上处处可导,且除去原点外导数不为零,因此,在z平面上除去原点外是处处保角的.下面讨论w = zn在原点的性质.若令z = reiθ,w = ρeiφ,则由ρeiφ =rnelnθ,得由此可知,在w = zn映射下,z平面上的圆周|z| = r映射成w 平面上的圆周|w|=rn,射线arg z =θ0 映射成射线arg w =φ=nθ0,正实轴θ =0映射......
2023-10-30
我们通常称z = x+iy为复数z的代数形式.除此之外,复数z还有多种表示形式,下面介绍复数的几种表示方法.
由于复数z =x+iy由一个有序实数对(x,y)唯一确定,在取定平面直角坐标系xOy时,实数对(x,y)可视为平面直角坐标系中的两个坐标组成的序对,这就建立了复数z与平面上的点的一一对应关系,于是对于任意一个复数z =x+iy,都对应于平面上的一点P(x,y),故可用实数对形式(x,y)表示.
由于所有实数与横坐标轴上的点一一对应,故我们称横坐标轴为实轴;同样地所有的纯虚数与除原点外的纵坐标轴上的点一一对应,故我们称纵坐标轴为虚轴.相对应于横,纵坐标所在的平面,我们把实轴,虚轴所在的平面称为复平面,或根据表示复数的字母z,w,··· ,称为z平面,w平面,···.显然,当y /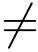 0 时,复数z 与
0 时,复数z 与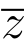 关于实轴对称.
关于实轴对称.
对于任意一个复数z都与平面上的点(x,y)对应,所以复数z也可以原点为起点,P(x,y)为终点的向量![]() 对应,即复数z可用向量表示,如(图1-1).
对应,即复数z可用向量表示,如(图1-1).
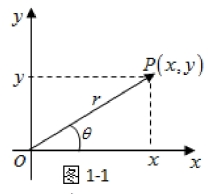
此时x和y分别是向量![]() 在实轴和虚轴上的投影.向量
在实轴和虚轴上的投影.向量![]() 的长度
的长度![]() 称为复数z =x+iy的模或绝对值,记作
称为复数z =x+iy的模或绝对值,记作
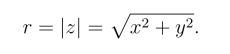
当z / 0时,以x轴的正方向为始边,向量
0时,以x轴的正方向为始边,向量![]() 为终边的夹角θ称为复数z的辐角,记作Argz = θ.我们知道,以x轴的正方向为始边,
为终边的夹角θ称为复数z的辐角,记作Argz = θ.我们知道,以x轴的正方向为始边,![]() 为终边的角有无限个,它们之间可以相差2π的整数倍,所以Argz有无穷多个值,即若θ1是复数z的任意一个辐角,则
为终边的角有无限个,它们之间可以相差2π的整数倍,所以Argz有无穷多个值,即若θ1是复数z的任意一个辐角,则
![]()
在复数z 的全部辐角中,我们把满足-π <θ0 ≤π 的辐角θ0 称为Argz的主值,记作θ0 =arg z.
因此,对于任意非零复数z,
Argz =arg z+2kπ,k为任意整数.
当z = x+iy 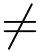 0 时,幅角的主值可根据反正切
0 时,幅角的主值可根据反正切![]() 的主值
的主值![]() 确定:
确定:

注:当z =0时,辐角无意义.
例1 求Arg(1+i)及![]()
解 Arg(1+i)=arg(1+i)+2kπ =![]() k为整数;
k为整数;![]() 为整数.
为整数.
设r,θ分别为非零复数z = x+iy的模和辐角,由直角坐标与极坐标的关系:
x=r cos θ,y =r sin θ,
可把复数z表示成下面形式:
z =r(cos θ+i sin θ),
称为复数z的三角形式.(www.chuimin.cn)
利用欧拉(Euler)公式:eiθ =cos θ+i sin θ,又可以得到
z =reiθ,
称为复数z的指数形式.
复数的各种表示法可以相互转换,以适应讨论不同问题时的需要.
例2 将下列复数化为三角形式与指数形式.
(1)z =-3i;(2)z =-1-i;(3)z =![]()
解 (1)显然,![]() 因此z的三角形式为
因此z的三角形式为
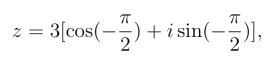
z的指数形式为
![]()
(2)由![]() 知,z 的三角形式为
知,z 的三角形式为
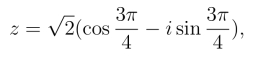
z的指数形式为
![]()
(3)易见r =1,由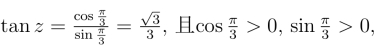 所以
所以
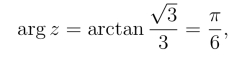
故z的三角形式为

z的指数形式为
![]()
有关复变函数及其应用的文章

幂函数w =zn(n ≥2为自然数)在z平面上处处可导,且除去原点外导数不为零,因此,在z平面上除去原点外是处处保角的.下面讨论w = zn在原点的性质.若令z = reiθ,w = ρeiφ,则由ρeiφ =rnelnθ,得由此可知,在w = zn映射下,z平面上的圆周|z| = r映射成w 平面上的圆周|w|=rn,射线arg z =θ0 映射成射线arg w =φ=nθ0,正实轴θ =0映射......
2023-10-30

如果是极点,指出它的级.解 令ζ = 则由于g(ζ)在ζ = 0解析且g 0,所以ζ = 0是的简单极点,因此z = ∞是f 的简单极点.......
2023-10-30

复变函数导数的定义在形式上与一元实变函数一致.定义1 设函数w = f(z)在点z0的某个邻域内有定义,且z0+△z是该邻域中的点,如果极限存在,我们称f(z)在点z0处可导(或可微),并称此极限值为f(z)在z0 点处的导数,记作若函数w = f(z)在点z0可导,导数为f′(z0),那么对于任意给定的ε >0,相应地存在δ(ε)>0,使得当0 <|△z|<δ时,有若函数w =f(z)在区域D内......
2023-10-30

设z1 =r1eiθ1,z2 =r2eiθ2,··· ,zn =rneiθn是n个非零复数,用数学归纳法可以得到这n个复数的乘积为特别地,当这n个复数相同时,我们把n个相同的复数z的乘积称为z的n次幂,记作zn.设z =reiθ,则zn =rneinθ =rn(cos nθ+i sin nθ).当r =1时,即z =cos θ+i sin θ,有(cos θ+i sin θ)n =cos nθ+i......
2023-10-30

从复积分的定义,可以推得复积分具有下列基本性质,它们与实变函数中定积分的性质类似.若复变函数f(z)和g(z)沿其积分路径C可积,则有1° f(z)±g(z)沿C可积,且有2° 对任意复数A=a+ib,函数Af(z)沿C可积,有3° f(z)沿C的反向曲线C-可积,且有4° (复积分对积分路径的可加性)若函数f(z)沿曲线Ck(k =1,2,··· ,n)可积,且C 由Ck依次连接而成,则f(z)......
2023-10-30

函数f(z)关于闭曲线C的对数留数是指积分这里需要假定函数在C上解析.显然当C为简单正向闭曲线时,上述对数留数就是对数函数Lnf(z)的导数在C内部各个孤立奇点处留数之和.函数f(z)关于简单闭曲线C的对数留数与它在C内部的零点和极点的个数有密切的联系.即定理1 若函数f(z)在正向简单闭曲线C 上解析且没有零点,又在C的内部除有限个极点外解析,则有其中N与P分别是f(z)在C内部零点和极点的总个......
2023-10-30

定理3 设函数f(z)在实轴上无奇点,且在上半平面除有限个奇点z1,z2,··· ,zn外解析,若存在正数M和r,使当|z|≥r且Imz ≥0 时,函数f(z)解析且有则有证明 设CR为上半圆周: z = Reiθ(0 ≤θ ≤π),取充分大的R使R ≥r,并且奇点z1,z2,··· ,zn均在由CR 及实轴上从-R到R的一段所围成的半圆内,则由留数定理得只须证明当R →+∞时,上述沿CR 的积分......
2023-10-30

定理2 设f(z)在实轴上解析,在上半平面Imz >0除有限个奇点z1,z2,··· ,zn 外解析.若存在正数r,M 和α >1,使当|z| ≥r 且Imz ≥0 时f(z)解析且满足|f(z)|≤M/|z|α,则积分I2 =存在且有证明设CR为上半圆周z = Reiθ(0 ≤θ ≤π),取充分大的R 使R ≥r并且奇点z1,z2,··· ,zn均在由CR及实轴上从-R 到R 的一段所围成的闭路......
2023-10-30
相关推荐