(一) 数列的概念定义1按照一定顺序排列的一列数a1,a2,…......
2023-11-17
我们在前面的章节里已经多次谈到过无穷数列和无穷级数,这一章,我们将作进一步了解——先稍稍正式地说一下它们的意思,然后讲几个有意思的例子。
所谓无穷数列,通俗地说就是一列“无穷无尽”的数。换句话说,就是对无论多大的自然数n,数列都有对应的项an。如果在n越来越大,趋于无穷的过程中,数列的通项an无限接近于数A,那么我们就说数列是收敛的,它的极限是A。否则,我们就说数列是发散的。
所谓无穷级数,简单说就是一个无穷的和式:a1+a2+…+an+…。如果将这个和式的前n项和记为Sn,则我们得到级数的部分和数列{ Sn}。如果这个部分和数列有极限A,我们就说级数是收敛的,级数的和等于A。如果一个级数不收敛,那么它就是发散的,因此也就没有所谓的级数和。
我们来考虑储蓄的利息问题。假设我们在银行存入1元钱,年利息为a。那么很简单,到期时的本利总和等于1+ a。如果银行说每半年利息为a/2,续存时利息计入本金,那么情况与前面所说的年利为a就不一样了。因为,这回如果我们存满一年,则会结息2次,半年时本利总和等于1+a/2,到满一年的时候,本利总和就是(1+a/2)2了。
相似地,如果银行说每四个月(即1/3年)的利息是a/3,那么一整年的本利和就会变成(1+a/3)3。如果每季度利息为a/4,一整年的本利总和相应地就会是(1+a/4)4。而如果每天的利息是a/365,那么年底的本利总和就将是(1+a/365)365。
总之,把年利a分成n等分作为每n分之一年的利息,则一年结束时的本利总和等于(1+a/ n)n。这就是“复利”概念的涵义。因此,我们提出一个数学问题:如果数列{en }的通项公式是
那么这个数列有没有极限?如果有,极限是多少?简单起见,我们下面讨论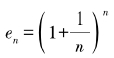 的情形。
的情形。
首先,根据二项式展开式,我们有:
即
相似地,我们展开en+1,然后去掉最后一项,就得到
这很明显告诉我们这样一个事实:
en+1>en。
也就是说,数列是单调增的。
其次,由以上en的表达式很容易得到:
不难发现,
这样,我们就得到第二个结论:
en<1+1+1=3。
因此,数列{en }是单调递增有上界的,它是有极限的。那么,这个极限是什么呢?我们把这个极限记为e,这个数在本书里已经出现过,它是一个无理数,而且与π一样是超越数,具体数值是2. 7182818…。
上一章我们提到一个和等于e的级数:
事实上,高等数学告诉我们一个更一般的结果:
回到利息问题,我们知道,如果年利是a,然后将年利作365等分,按日计利,并且利息逐期计入本金,那么一年后的本利总和就成为 ,这个数值相当接近于ea。
,这个数值相当接近于ea。
从上述ea的表达式看,如果a很小,那么前三项之后的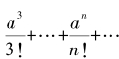 部分在实际计算中就会小到可以忽略不计,但如果年利比较高,则它们的差别就会相对大一些。下面,我们以年利为a=5%以及a= 30%为例,将几种本利总和的数值列为如下表格:
部分在实际计算中就会小到可以忽略不计,但如果年利比较高,则它们的差别就会相对大一些。下面,我们以年利为a=5%以及a= 30%为例,将几种本利总和的数值列为如下表格:
上一章我们讨论了无穷连分数,在所有可能的无穷连分数展开式中,全部由1构成的连分数可以算是“最简单”的:
如果我们记这个连分数的值为x,则有
因此
x2-x-1=0。
这个一元二次方程有两个解,取它的正解,我们得到:
计算这个连分数的渐进分数,将得到如下序列:
这个渐进分数序列的规律是很明显的,我们可以瞬间观察到,每个分数的分子都与下一个分数的分母相同。而分母的序列是:
1,1,2,3,5,8,13,21,34,55,89,144,233,…
13世纪的数学家,意大利比萨城的列昂纳多另有一个名字叫作斐波那契,这个数列就是以他的名字命名的,称为“斐波那契数列”。斐波那契数列非常著名,它不仅以前已经被深入研究,而且至今仍然是数学爱好者经常探讨的主题。
一般人们把斐波那契数列的通项记为Fn,通项的下标则通常从零算起。也就是说,人们通常规定F0= 1,F1= 1。在这两项之后,斐波那契数列其他的每一个数都等于其前两个数之和,即
Fn=Fn-1+Fn-2。
在大自然中我们不时会遇到这个数列,它在动物与植物的生长规律中经常出现。例如,一棵树以如下这种形式生长:包括主干在内的每一条老枝每过一个时段就长出一条新枝;每一条新枝在它出现的第一个时段内不生长新的分支,第二个时段开始则成为能长出新枝的老枝之一。这样的生长形式可以画成如下示意图,而该树生长经过n个时段后的树枝总数就等于Fn。
斐波那契数列有大量很容易推得的性质,而更多性质的推导也只不过略有难度。最简单的性质之一是:前n+1个斐波那契数之和等于Fn+2-1,即:
F0+F1+…+Fn=Fn+2-1。
等式的证明很简单。根据数列的递推公式,我们有:
F1=F2-F0
F2=F3-F1
F3=F4-F2
……
Fn-1=Fn-Fn-2
Fn=Fn+1-Fn-1
Fn+1=Fn+2-Fn
我们把上述等式相加,则右边经过一系列相互抵消之后,我们得到:
F1+…+Fn+Fn+1=Fn+2+Fn+1-F1-F0,由F1=1,将右式中的F0移项即证明等式。
此外,斐波那契数列还有无数有趣的性质,这个数列是如此地吸引着数学爱好者,以致苏联数学家著有关于这个数列的专著,而热心者于1963年成立的斐波那契协会,至今仍然是一个颇为活跃的民间团体。可以说,关于斐波那契数列的性质我们无论如何都无法做出相对完整的介绍。因此,我们下面只列举它的少数几个有趣的性质:
这个以及随后的两个等式都很容易用数学归纳法来证明,因此我们对它们的证明都略而不论。
在上述式(2)中,我们用[x]表示不超过x的最大整数。因此,这个等式告诉我们,斐波那契数列的第n项是[n/2]+ 1个二项式系数的和,这些二项式系数在杨辉三角中处在一条上升的斜线上。斐波那契数列与杨辉三角的这个关系非常地出人意料,它可以用下图表示:
斐波那契数列的这个性质有一个很有趣的几何表示:我们从两个单位正方形出发,然后接上一个2×2的正方形,之后再接上一个3×3的正方形……如此不断进行下去,则我们将得到一个如右所示的图形。假如我们凑巧在接上8×8的正方形后停止,则我们得到一个8×13的矩形。图形中的面积间有如下关系:
在上一章中我们讨论过2的连分数展开,其渐进分数有如下递推公式:
因此,它的分子与分母两个数列满足如下条件:
从后一等式可以得到:
bn+1-bn=an,
因此,
这样,我们就得到一个关于2连分数展开渐进分数的分子数列{an}的递推公式:
an+2=2an+1+an。
简单计算前两个渐进分数,可知:a0= 1,a1= 3。至此我们发现, {an}与斐波那契数列的通项公式很相似,它们的an+2都等于某种an+1与an的简单倍数和。正因为这种相似性,两个数列的通项公式形式也很相似,求解通项公式的方法也相同。下面,我们以{an}为例来介绍一种初等的求解通项公式的办法。
我们设想{an}的递推公式an+2= 2an+1+an可以写成如下形式:
an+2-ran+1=s(an+1-ran)。
与递推公式对比,我们得到:
r+s=2,rs=-1。
因此,r和s是一元二次方程
x2-2x-1=0
的解。由于r和s的地位是对称的,因此我们可以得到两组解:
令un=an+1-r1an,vn=an+1-r2an,则我们得到两个等比数列:
un+1=s1un, vn+1=s2vn。
计算两个数列的第一项u0和v0,我们得到:
于是,由等比数列的通项公式,就有:
因此,
另一方面,由un和vn的定义知,
所以,我们最终得到
这样,我们就求出了{an}的通项公式,它的值事实上等于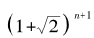 的有理部分。
的有理部分。
我们不难推导出,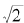 连分数展开之渐进分数的分母数列{bn }拥有与分子数列{an}一样的递推公式,不同的是最初两项的数值不同:b0=1,b1= 2。因为这个不同,通过以上步骤所求得的{bn }的通项公式是:(www.chuimin.cn)
连分数展开之渐进分数的分母数列{bn }拥有与分子数列{an}一样的递推公式,不同的是最初两项的数值不同:b0=1,b1= 2。因为这个不同,通过以上步骤所求得的{bn }的通项公式是:(www.chuimin.cn)
正如我们前面所说的,斐波那契数列的通项公式也可以用同样的方法求得,它的具体表达式是:
从这个斐波那契数列的通项公式很明显可以看出,数列{an}与{bn }确实与斐波那契数列非常相似。然而,从连分数的角度看有一点非常不同: {an}与{bn }分别对应2连分数展开的分子和分母,而斐波那契数列则可以说是同时对应着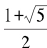 连分数展开的分子和分母。事实上,对这类与连分数展开相对应的数列而言,它们的很多有趣性质是同时与分子数列和分母数列相关联的,只不过因为斐波那契数列同时对应着相应的分子与分母,所以它的趣味性质中才只出现一个数列。明白了这一点,我们就会理解, {an}与{bn }的很多性质在形式上与斐波那契数列有所不同,这些性质中往往{an}与{bn }同时出现。然而无论如何,关于{an}与{bn}的趣味性质同样是多不胜数,我们只能略举几个例子:
连分数展开的分子和分母。事实上,对这类与连分数展开相对应的数列而言,它们的很多有趣性质是同时与分子数列和分母数列相关联的,只不过因为斐波那契数列同时对应着相应的分子与分母,所以它的趣味性质中才只出现一个数列。明白了这一点,我们就会理解, {an}与{bn }的很多性质在形式上与斐波那契数列有所不同,这些性质中往往{an}与{bn }同时出现。然而无论如何,关于{an}与{bn}的趣味性质同样是多不胜数,我们只能略举几个例子:
斐波那契数列是用递推公式定义的,因此我们可以编写使用“递归”函数形式的计算机代码,用来计算斐波那契数列第n项的数值。但是,如果没有经验,写出来的代码有可能让计算机累到吐血。例如,如果我们这样写代码:
那么,计算机的计算量将会是无比巨大。事实上,为了计算斐波那契数列第n项的数值,上述函数“斐波”调用了它自己去计算第n-1项和第n-2项。因此,如果我们把“斐波”计算第n项所用的计算量记为T(n)的话,粗略地说,我们就有这样的关系:
T(n)= T(n-1)+T(n-2)。
这样一来,这个计算量就是一个与斐波那契数列的第n项相似的数。我们从斐波那契数列的通项公式知道,它是一个关于n的底数大约为1. 618的指数函数,而指数函数增长是非常非常快的,如果我们用这个函数计算T(100)的话,计算量将达到10的20次方的量级,这在一般的计算机上是几年都算不出来的!
计算机科学中有一个称为“计算复杂度”的概念,它表示的是计算机程序在输入的规模为n时计算量与n的函数关系。在编程界,计算复杂度为指数函数的情况是绝对不可接受的。因此,这个例子提醒初学编程的读者:务必注意考虑自己所编写程序的计算复杂度。它不是代码看起来是否复杂,而是运行时到底会进行多少计算。
那么,有没有好一些的算法呢?答案是肯定的。仔细研究上述函数“斐波”的代码,我们发现:它计算F(n)时计算了F(n-1)和F(n-2),而计算F(n-1)时又计算了F(n-2)和F(n-3)。因此,F(n-2)被重复计算了!再仔细考察,我们会发现所有F(n-2)以下的项都被重复计算,而且越后面的项被重复计算的次数越多,最后多到让计算机无法承受!发现了问题所在,解决方法就容易找到了——我们只要存储当n较小时的F(n)值,就可以避免如此海量的重复劳动了。根据这个思路,不难编写出计算量很小的代码,学习编程的读者可以自己尝试。从我们已经介绍过的内容看来, 是一个很特别的数,它是三角形数,是从1到n所有自然数的和,它的平方等于从1到n所有自然数的立方和。此外,它还是组合数
是一个很特别的数,它是三角形数,是从1到n所有自然数的和,它的平方等于从1到n所有自然数的立方和。此外,它还是组合数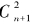 。而在第7章介绍的关于连续自然数的趣味和式中,它也在两个著名的等式中露面。不仅如此,以它的倒数为通项的级数,是为数不多的几个通过初等方法可以求得和值的级数:
。而在第7章介绍的关于连续自然数的趣味和式中,它也在两个著名的等式中露面。不仅如此,以它的倒数为通项的级数,是为数不多的几个通过初等方法可以求得和值的级数:
这个级数的求和方法很简单,我们在求数列 极限的时候事实上已经做过。
极限的时候事实上已经做过。
然而,如下的级数虽然也与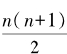 有关系,却没有可以用来求和的初等办法:
有关系,却没有可以用来求和的初等办法:
这个级数的和等于ln2,但是我们需要具备大学数学中关于幂级数的知识,才有足够的工具来求出这个和,所以我们这里只能略而不论。
考虑级数
如果我们把它的通项依次两两配对相加,则会得到前述那个等于ln2的级数。因此,这两个级数的和是相同的。但是,读者需要注意的是,这两个级数虽然和的数值相同,它们是截然不同的两个级数,绝对不能混淆!
事实上,这两个级数的通项不同,部分和数列也不同。而且,很重要的一点是:前一个级数的每一项都是正的,是一个“正项级数”;而后一个的通项则正负交替出现,因而是一个“交替级数”。
如果我们考虑将后一个级数中的正项全部去掉,则留下的级数是:
这个级数恰好是以前我们提到过“调和级数”的负1/2倍。由于调和级数是发散的,因此这个级数也不会收敛。这就是说,级数
中的负项组成的级数是发散的,而由于原级数是收敛的,所以它的正项构成的级数也是发散的。这样的级数很有意思——通俗地说,它的正项的“和”是“正无穷大”,而负项的“和”则是“负无穷大”。因此,如果我们通过调换它的通项顺序来构造新的级数,那么我们就可能得到不同的级数和,甚至得到发散的级数!
举一个例子,我们用如下的方法来重排这个级数的通项:
(1)先按顺序挑出正项,直到部分和超过π值为止;
(2)接下来按顺序放置负项,直到部分和小于π值为止。由于原级数的正项的“和”是“正无穷大”,因此不断重复步骤(1)是完全没有问题的。而由于负项的“和”是“负无穷大”,因此我们也总是有负项可以进行步骤(2)。因此,虽然这个方法看似是“寅吃卯粮”地使用正项,但由于正项有无穷多个,步骤(1)和(2)都可以无限地重复进行下去。那么,这样构造出来的新的级数是不是收敛的呢?答案是肯定的。它的和是多少?猜也能猜出来,级数和等于π!
这个例子可能让读者很惊讶,但这正体现出这种无穷级数的特点——这种级数称为“条件收敛”级数,对它的通项的适当重排可以使重排后所得的级数收敛于任何指定的数值!需要指出的是,稍前提到的那个与本例级数和相同的正项级数没有这个有趣的性质,它不管如何重排,总是会得到相同的级数和。
我们已经再次不加证明地提到如下等式:
现在,我们用初等的方法来证明它。
对 ,我们已经知道,数列{en }的极限是e。
,我们已经知道,数列{en }的极限是e。
这里我们定义一个新的数列,它的通项是:
由于 的极限等于1,而
的极限等于1,而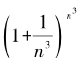 是
是 ,当n趋于无穷时的极限等于e。因此,数列{hn}的极限也等于e。将
,当n趋于无穷时的极限等于e。因此,数列{hn}的极限也等于e。将 用二项式定理展开,然后我们舍去第n+1项之后的所有项,则有:
用二项式定理展开,然后我们舍去第n+1项之后的所有项,则有:
进一步减小不等式右边的值,我们得到:
用数学归纳法不难证明,如果α1,α2,…αn都是大于0而小于1的数,则成立着如下的不等式:
(1-α1)·(1-α2)·…·(1-αn)>1-(α1+α2+…+αn)。对关于 可得到:的最后那个不等式应用这个结论,我们立
可得到:的最后那个不等式应用这个结论,我们立
因此,我们有:
这样,我们很容易得到:
此外,我们在讨论数列{en }时曾经证明:
因此,
而由于{en}与{hn}的极限都是e,因此,当n趋于无穷时,和式 的极限也必然是e。也就是说,我们终于证明:
的极限也必然是e。也就是说,我们终于证明:
数学中有很多很多有意思的东西,有些是关于数字的等式,有些是抽象的公式,有些则是解题技巧或思维方式。我们这本小书至此就要结束了,希望我们的读者不仅品尝到数学的趣味,学到一些数学知识,而且也学会一些有益的思考方式。作为本章以及全书的结束,我们最后列举一些有趣的级数,在结束前再一次让大家欣赏数学的奇趣。
泰勒级数
无穷级数就是一个无穷和式a0+a1+a2+…an+…。如果它的通项为an是数值,那么它就是一个“数项级数”。例如, 就是一个数项级数。如果级数的通项an是自变量x的函数,那么这个级数就是一个“函数项级数”。对每一个自变量x的取值,函数项级数对应一个数项级数。因此,这些数项级数收敛的地方,函数项级数就收敛于一个函数。
就是一个数项级数。如果级数的通项an是自变量x的函数,那么这个级数就是一个“函数项级数”。对每一个自变量x的取值,函数项级数对应一个数项级数。因此,这些数项级数收敛的地方,函数项级数就收敛于一个函数。
通项为an= cnxn的函数项级数是很特别的,它们称为“幂级数”。幂级数中最重要而有趣的是“泰勒级数”,我们下面列举常见的几个:
所有-1<x<1成立。
泰勒级数的两种用途
泰勒级数是非常重要的数学工具,这里我们来介绍它们的两种用途:一是求数项级数的和,二是用作近似计算。
第一种用途的例子是我们本章最后所列级数中的(1)、(2)、(13)、(14)、(15)、(18),它们可以从上述的(1)、(8)、(5)、(6)等公式得到。
对于第二种用途,我们可以举两个例子。首先以sinx为例。对于比较小的x,我们可以用sinx≈
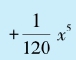 进行近似计算。例如,对
进行近似计算。例如,对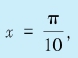 我们有
我们有 。
。
0. 30901699…,可见这个近似公式的精确度相当高。
根据上列第(7)式,对于小的x,我们可以用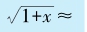
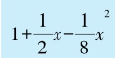 作平方根的近似计算。比方说,我们想近似地计算
作平方根的近似计算。比方说,我们想近似地计算 。那么,我们可以把
。那么,我们可以把 写成
写成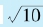 =
=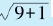 =。这时,采用近似式
=。这时,采用近似式 ,我们就得到
,我们就得到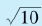 ≈3×1. 0540 = 3. 1620。
≈3×1. 0540 = 3. 1620。
傅立叶级数
函数项级数中,如果第n项是形如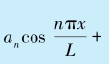 的函数,则这种级数就称为傅立叶级数。傅立叶级数在数学、物理学与工程学中都非常重要,我们这里举一个例子:
的函数,则这种级数就称为傅立叶级数。傅立叶级数在数学、物理学与工程学中都非常重要,我们这里举一个例子: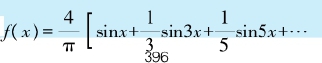
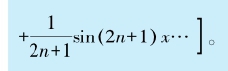
这是一个周期等于2π的函数,其图形如下:
换句话说,就是:
π级数
将x=π/2代入上述级数,我们得到:
即
这就是本章正文最后部分的第(2)个级数。
很显然,这种级数可以用来求π的近似值。但是,这个级数的“尾部”的数量级是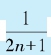 ,它不能快速地得到π的高精度近似值。
,它不能快速地得到π的高精度近似值。
为了快速求得π的高精度近似,数学家们发掘出很多关于π的级数。这些数学家中,100年前印度的拉玛努金是历史上最著名的,而南京大学的孙智伟教授则在近年来取得更为惊人的成果。以下两个公式中,第一个是拉玛努金发现的,而第二个则是孙智伟教授的杰作:
其中,
更多的连续自然和等式
在第七章我们列出了几组有趣的自然数连续和等式,但那只是这类趣味等式的冰山一角。事实上,这类等式有无穷多组,我们下面再举两个例子。
对任何自然数s,从3s2-1到3s2+3s+1这(3s+3)个连续自然数的和,等于从3s2+3s+2到3s2+6s+1这3s个连续自然数的和。换句话说,我们可以列出如下趣味等式:
2+3+…+7=8+9+10,
11+12+13+…+19=20+21+…+25,
26+27+28+…+36+37=38+39+…+45+46,
47+48+49+…+60+61=62+63+…+72+73,
……
对任何自然数n,从10n2+10n-2到10n2+20n+12这(10n+15)个连续自然数的和,等于从10n2+20n+13到10 n2+30n+17这(10n+5)个连续自然数的和。换句话说,我们可以列出如下趣味等式:
18+19+…+42=43+44+…+57,
58+59+60+…+92=93+94+…+116+117,
118+119+120+…161+162=163+164+…196+197,
……
连续自然和等式的一般公式
连续自然和等式的一般公式有两类,它们的推导并不是非常困难,我们在这里给出其中的一类:
对奇数w, q,令u=q·w2,m=q·w·s,取k=q·s2-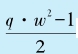 ,则从k开始(m+u)个连续自然数的和,等于从(k+m+u)开始m个连续自然数的和。
,则从k开始(m+u)个连续自然数的和,等于从(k+m+u)开始m个连续自然数的和。
有关如数加珍:数字丛林的冒险之旅的文章

而马氏言今本《参同契》为后人伪托其名所作且与原本揉合为一,则其理由皆不足。历来文献皆持魏等著《参同契》,非可谓全出伪托,自应有其所本;《参同契》依托纬候,与黄老并论,正是成书于汉代......
2024-05-04

任务描述在Pro/E 5.0的草绘类别中使用直线命令,绘制如图1-1-1所示契铁块的二维视图,并以“1-1-1”为文件名命名保存。图1-1-1契铁块任务实施一、Pro/E 5.0软件的启动图1-1-2启动图标方法1双击桌面图标,即图1-1-2所示“proeWildfire 5.0.exe”快捷方式图标。步骤1绘制第一条水平线。图1-1-17文件保存图1-1-18保存对象以上就是图1-1-1的整个绘制操作方法。......
2023-06-15

,umn+1中,或者存在一个长度大于m的减子数列,或者存在一个长度大于n的增子数列.证明:分别用l-i,l-i表示从ui开始的最长的减子数列和最长的增子数列的长度.假设命题的结论是错误的,即每个减子数列的长度不超过m,并且每个增子数列的长度不超过n.定义一......
2023-11-22

Gartner公司在2018年和2019年十大战略性科技发展趋势中将数字孪生作为时下重要技术之一,其对数字孪生描述为:数字孪生是现实世界实体或系统的数字化表现。Gartner公司认为,一个数字孪生概念至少需要四个要素:数字模型、关联数据、身份识别和实时监测功能。......
2023-10-30

达契亚战争早在图密善在位的时候,位于今天罗马尼亚一带的达契亚人就曾经越过多瑙河侵入罗马帝国境内。公元101年,他集结了11个军团大约15万人的兵力——这是迄今为止罗马人在一次战役中所动员的最大力量,跨过多瑙河对达契亚人发起进攻。战争持续了五年。第一次跨越多瑙河的时候,罗马人是通过架设浮桥走过去的。桥面距离水面的高度约为27米,桥下可供船只正常通行。达契亚国王战败自杀,达契亚全境被并入罗马疆域。......
2023-09-21

数字孪生城市是通过数字孪生技术在城市层面的广泛应用建立起来的。数字孪生城市就是通过构建城市的物理世界和网络虚拟空间的复杂系统,一对一的通信,相互映射和协作交互,在网络空间中创建匹配和对应的模型。数字孪生城市的本质是虚拟空间中对城市的映射,也是支持新型智能城市建设的复杂综合技术体系和信息维度中虚拟城市在物理维度和虚拟城市中的共存,虚拟和真实集成。......
2023-10-30
相关推荐