连分数展开：数字丛林的冒险

现在，我们回过头来，重新考察一下第3章提到的辗转相除法。当时，我们用这个算法证明15与49是互素的，即它们除了1之外没有别的公因数。算法中的第一个操作是用15来除49。换一个写法，这一步可以写成

根据这个算法，接下来我们要用4来除15。为了将这个除法运算写成新的形式，我们将它写成

下一个除法是以3除4，我们再次倒过来写：

由于已经得到公因数为1，通常我们在这里就停止了。我们有时会再多做一步，但如果那样做，我们就会因为3可以被1整除而得到余数为0，而这也是在公因数为1时辗转相除法终止的步骤。

上述多层分数的表达式

称为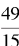的“连分数展开式”。我们已经看到，它与辗转相除法有着密切的联系。

假设我们现在删去最后一个分数，然后计算余下的分数，则得到

这个分数自然不会等于一开始的分数49/15。当然，我们也不会期望它们相等，我们因为扔掉了而改变了原来的分数。两个分数不相同，然而它们相差多少呢？答案是相差不多，即

扔掉那个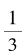所导致的表达式改变值仅有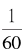。但那也许是运气？我们因此再试一试另一个数：

这回最后一个分数部分是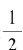，它也是我们后面要扔掉的部分。扔掉最末这个分数，整理所得的连分数，则得

为了比较，我们像前面一样从77/34中减去这个分数：

这个差的值比前一例还要小，并且还是一个负数。事实上，重要的事情不在于差值的大小，而是两个例子里这个差的分子都是1。

这不是巧合。虽然我们省略了，但是不难证明，当分数的分子与分母互素时——即约分到不能再约时，如上所得之差的分子都会恰好等于1。

从这个简单的事实出发，我们可以得到若干意料之外的结果。

线性方程

49x-15y=1

有无穷多组（x，y）为其解：只要选择一个x代入，然后解出y即可，问题是它们往往不是整数解组。那么，这个方程有丢番图解吗？也就是说，有没有整数对（x，y）满足这个方程？答案是肯定的，我们刚才就找到了一组，即x = 4， y= 15。倒回去一两页纸，我们会看到如下等式：

两边同时乘以60，即得到

49×4-13×15=1。

在这里，找出数对（4，15）的方法是用连分数展开，它本质上和辗转相除法等价。事实上，我们在第4章讨论同余方程时，就已经用辗转相除法求解了。

然而，上述方法使用起来还需小心，假如原始方程是

77x-34y=1，

那么以上步骤得到的是：

77×15-34×34=-1，

这与原来方程的解差了一个负号。不过，我们的工夫并没有白费，它已经提供了解决问题的办法。如果用连分数的想法，我们只要将77/34的连分数展开再额外进行一步就可以了。换句话说，我们把写成

然后去掉式子里的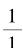，就可以得到方程的一个解：

像前面那样计算差值，即有

由此即得

77×19-34×43=1，

因而x=19，y=43是方程的一组解。

需要说明的是，这个解也可用另一个更为浅显的办法得到：从连分数我们已经得到等式

77×15-34×34=-1，

它可以写成

77×（-15）-34×（-34）= 1。

所以x=-15，y=-34是方程的一组非正整数的解。但是，在方程左边添加77×34-34×77这样一个值等于0的式子，我们就会得到：

77×（34-15）-34×（77-34）= 1，

由此同样可得到x=19，y=43这组解。

为什么会有人想要得到（正）整数解？因为人类认识数字是从整数开始的，也因为整数在日常生活中更让人习惯，也更方便。事实上，中国古代数学书中偶尔会出现这类算题。这里，我们抛开古人的原题，自己来仿造一个体现“现实”生活场景的算题：

狐皮裘一件的价格是77个钱，羊皮裘一件的价格是34个钱。某人发现他所有的钱刚好可以买若干狐皮裘，但买若干羊皮裘后会剩下一个钱。问题是：这个人总共有多少个钱？

如果把狐皮裘的件数记为F，而羊皮裘的件数记为G，则我们可以列出等式

77F=34G+1，

或

77F-34G=1。

而我们刚刚得到F = 19，G = 43是满足方程的解。因此，这个人总共有77×19 = 1463个铜钱——看来，问题中的这个人是个做皮衣生意的。

然而，正如我们前面所做的，我们可以在方程的左边任意添加任意多个77×34-34×77，因此（19，43）并不是方程唯一的解。我们不难发现，方程有这样的通解：

F=19+34N，

G=43+77N。

如果算题里的这个人真是做皮衣生意的，说不定他的生意比较大，因此他的钱足够买F= 19+34= 53件狐皮裘也是可能的。所以严格地说，这个问题的答案不能唯一肯定。

问题的这些解在几何上的图形也饶有趣味。（19，43）这个点两个坐标都是整数，是平面上的“格点”，就是平面上坐标为整数的水平线与铅直线构成的坐标网格上的交点。线性方程

77x-34y=1

的图形是一条通过格点（19，43）的直线。这条直线通过无穷多个格点，沿着“正方向”的下一个格点是（53，120）。

如果a和b互素，那么正如我们上面所指出的，不定方程

ax-by=1

会有无穷多个解。因此，方程

ax-by=c

同样也有无穷多个解。因为我们只要解出前一个方程，然后把它的解乘以系数c就可以了。而如果a与b不是互素的，那么不难证明，后一个方程有（整数）解的充分必要条件是：c可以整除a与b的最大公因数。当然，有解的时候解也会是无穷多个。

虽然我们总是可以把有限的连分数展开式逐步化简成单个分数p/ q，但任何无理数显然都不可以写成有限的连分数展开式。所以，如果一个无理数被写成连分数展开式，那么这个展开式必定是无穷尽的。我们下面来考察某些无理数的连分数展开。

您觉得我们首先应该考察哪种无理数？也许，我们的看法是一致的：应该先考察平方根。但是，为了显得有点儿个性，我们要先把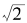放在一边，先来考察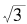的连分数展开。

我们首先对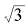加上1再减去1，由于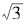值的整数部分等于1。于是，

我们在将分数写成连分数时用了颠倒分数的做法，因此，对上式中小于1的部分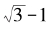，我们也依样画葫芦：

现在，末尾分数的分母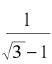可以通过乘上而有理化：

这就是说，

我们看到，后面分数的分母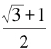

是一个大于1的数，它可以写成一个正整数加上一个小于1的正数，即

接下来，我们再次依样画葫芦，把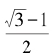写成倒数的形式，并且有理化它的分母：

我们得到：

这回，我们在最后一个分式的分母里看到了一个熟悉的小于1的部分：

回顾上面的运算过程，我们有：

因此，我们可以把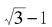的这个式子代入到最后得到的分数里，也就是说，我们有：

事实上，没有什么理由可以阻止我们这样重复下去。所以，我们勇敢地让它无限地继续下去，最终得到：

无穷的连分数形式的具体意义是什么？其实没有什么神秘的，它表示了一个通项是有限连分数的无穷数列，我们把这个连分数数列称为相应无穷连分数的“渐进数列”（注意，对连分数的情形我们用“渐进”而不是“渐近”）。如果这个数列有极限，那么我们就认为以上这个表达式确实就是的连分数展开式。为了考察这个有限连分数数列的变化趋势，我们来计算它最前面的几项：

……

我们继续坚持计算下去，希望从中发现什么规律：

好像看不出来？这不奇怪，因为规律不明显。但是，我们换个角度思考：既然我们认为这些分数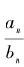应该会越来越接近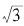，我们何不计算一下它们的平方与3的差距？这样一来，我们就有所发现了，代入以上几个分数计算所得的分别为：

这些分数中，正负符号交替出现，分子的值交替出现2与1，而分母则是原来分数分母的平方。因此，如果我们实施“去分母”运算，我们将得到：

以及

如果这两个由观察而总结的式子总是正确的话，那么我们就从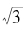的连分数展开式出发，找出了两个丢番图方程的所有解！那么，我们的式子到底对不对呢？答案确实是对的！事实上，从的连分数展开式我们不难得到这样的递推关系：

这个等式通分后变成

这个递推关系是不是似曾相识？确实是，它与我们在第5章讨论的递推公式很相似！在第5章我们指出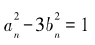，的最小解组是a₀=2，b₀=1，而其他解组可以由递推关系

a_n+1=2a_n+3b_n，b_n+1=a_n+2b_n

来确定。因此，我们得到这样的结果：的渐进连分数序列交叉出现两个相关的丢番图方程的解，两个方程的第一组解不同，但递推公式相同。

与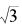相比，的连分数展开式要简单些，具体的推算和分析留给读者自己完成，我们仅在这里指出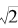： 的连分数展开式是

它的渐进连分数数列也对应着一对丢番图方程：

x²-2y²=±1。

我们下面来讨论一般非完全平方数平方根的连分数。我们用D表示一个非完全平方数，因此我们考虑的是的连分数展开式。首先，我们考虑一种特殊的情形，即考虑

D=n²+1

时的情形。此时，

不断迭代下去，我们得到：

因此，我们得到：

与D= n²+1情形略有些相似地，包括D = n²+2，D = n²-1在内的多个情形，其连分数展开式也不难得到。到底有哪些特殊情形？这个问题留给读者去探讨，我们其中的三个结果：

现在，我们来介绍计算一般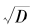连分数展开的具体步骤。记N₀为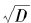的整数部分，则

其中，是一个大于0而小于1的无理数。记

M0=N₀， L₀=1，

由以下三个递推公式

我们依次计算L_k+1，N_k+1，M_k+1，则D的连分数展开式为：

在（2）式中，我们采用floor（x）表示不超过x的最大整数，举个例子，由于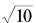=3.16…，所以floor（）= 3。

以上递推公式不难用数学归纳法来证明。很重要的一点是：对自然数的平方根而言，这个计算在有限步骤内就会重复。也就是说，对一般的，我们不需要无穷无尽地计算下去，若干步骤之后它就循环了。

对上面这个递推公式，我们来看一个具体的算例，我们来计算的连分数展开：(www.chuimin.cn)

M0=3， L₀=1，

由递推公式

依次计算，得到：

L₂=3，N₂=1，M2=2；

L₃=3，N₃=1，M3=1；

L₄=4，N₄=1，M4=3；

L₅=1，N₅=6，M₅=3；

L₆=4，N₆=1，M6=1。

由于k= 6时的L_k，N_k，Mk重复了k= 1时的数值，我们已经到达了连分数的循环节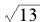，的连分数形式即为：

现在我们可以回答第2章的这个问题：什么样的完全平方数同时又是三角形数？当时我们发现三角形数是形如（n²+n） /2的数，然后提出这样一个问题：它们什么时候会是完全平方呢？

要求一个三角形数等于一个自然数的完全平方，那便是求丢番图方程的解。将方程两边同时乘以8，然后再同时加上1，则有

4n²+4n+1=8m²+1，

也就是说，

（2n+1）²=2（2m）²+1。

这个方程我们有办法求解，因为我们只要求出丢番图方程

x²-2y²=1

的整数解，然后从中找出y值为偶数时的解组就可以了。这个时候，我们得到x= 2n+1，y= 2m。计算几项就会发现，这些解组似乎是恰好在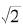连分数展开式的渐进分数序列中交替出现。我们知道

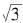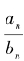与前文关于的分析相似地，如果的渐进连分数写成分数形式为的话，那么上述等式告诉我们，这些分数之间有如下递推关系：

这等于说，

从上述关系式出发很容易证明：如果a_n是奇数而b_n是偶数，则a_n+2是奇数而b_n+2是偶数。不仅如此，我们还发现，

因此，从a₁=3，b₁= 2出发，我们得到的所有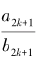都大于2，并且其中的b_2k+1都是偶数，所以它们都对应着同时是完全平方数的三角数。回顾前文，这等于说，从上述关于a_2k+1和b_2k+1的递推公式计算出来的每一个b_2k+1，它的一半的平方都是三角形数。例如，b₇= 408，它一半的平方是一个三角数：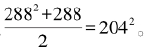

其实，从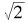的连分数表达式我们可以更简单地递推关系式，因为，从

可以得到

然而，

因此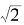，的渐进分数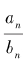确实是大于和小于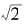交替出现。

我们不难证明，渐进分数列之偶子列对应的a_2k和b_2k恰好常满足丢番图方程x²-2y²= -1。事实上，这两个子列给出了相应两个丢番图方程的全部解。从上文我们看到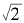，的连分数给出了两个丢番图方程

x²-2y²=1， x²-2y²=-1

的解，然而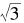，的连分数相对应的丢番图方程却是

x²-3y²=1， x²-3y²=-2。

那么，x²-3y²=-1和x²-3y²=2的解从哪里来？读到这里提出这个问题确实是恰逢其时。我们其实在第6章讨论过，x²-3y²=2是没有（正整数）解的，它甚至连有理数解也没有。同样地，x²-3y²=-1也没有解。

刚刚我们看到，形如x²-Ny²=±1的丢番图方程，有的有解有的却没有解。对正整数N，形如

x²-Ny²=1的方程称为佩尔方程。关于佩尔方程有这样的结论：

当N不为完全平方数时，佩尔方程有正整数解组。

但是，形如

x²-Ny²=-1

的方程当N= 2时有解，而当N= 3时却没有。这类方程对什么样的N有解是一个长而有趣的故事，我们不能在此完整介绍。但是，我们不能被N= 2和N = 3时的简单情形所误导，对有些不那么大的N，相应的连分数与丢番图方程都可能相当复杂。

这种复杂性可以以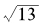作例子来说明。前面我们求出了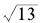的连分数展开，它的连分数分母的循环周期是5，这已经并不简单了，而相关的丢番图方程问题则更加繁复——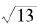的连分数展开式逐步计算，我们可以得到渐进分数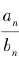

的递推关系式：

按照正负交替的规律，为了求解相应的丢番图方程，我们需要求a_n+2和b_n+2关于a_n，b_n的递推公式，因此，我们从上面的两个递推式再迭代一次，得到：

这里的系数很大，可见丢番图方程的解大概不会简单。不仅如此，我们发现它所导出的两个丢番图方程不是佩尔方程，而是如下的丢番图方程

x²-13y²=±4。

幸好，我们知道方程

x²-13y²=1

的解也会满足上面所推得的递推关系，因此从非负整数解x=1，y= 0出发，我们可以得到x²-13y²= 1的第一组正整数解：

x₁=649，y₁=180。

于是，我们可以用递推关系计算接着的两组解：

x₂=842401，y₂=233640；

x₃=1093435849，y₃=303264540。

你是不是会惊叫：怎么解的数值增长得那么快？是的，x²-13y²=1的后一组解大约是前一组的1300倍！

我们在第7章讨论过与3²+4²= 5²相似的连续自然数平方和等式，如果我们突发奇想，要求等式左边的项数是右边的两倍，结果会是什么？

我们假设，等式左边的自然数从（k+1）开始到（k+2m）结束，总共有2m个；右边的自然数从（k+2m+1）开始，而终止于（k+3m），总共有m个。这就是说，

（k+1）²+…+（k+2m）²=（k+2m+1）²+…+（k+3m）²。

化简这个等式，并从中解出k，我们得到：

这样，原来的问题就转化为这样的一个问题：什么时候141m²+3是完全平方数？或者说，我们需要求解如下的丢番图方程：

n²-141m²=3。

对应着“勾三股四弦五”的等式，我们知道这个方程的一个解是：n₀=12，m₀=1。那么怎么求这个丢番图方程的所有解呢？我们用连分数展开的方法，即依靠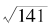的连分数展开的循环节来求解。

依照我们介绍过的公式计算，可以求得整数部分为11，循环节是：1，6，1，1，22。因此从对应的渐进连分数出发，我们得到：

n_t+1=18049n_t+214320m_t，

m_t+1=1520n_t+18049m_t，

根据已知的n₀=12，m₀=1，应用上述公式可以求得：

n₁=430908，m₁=36289，

因此，

k₁=3768×12+44744×1+2=89962。

这就是说，在我们突发奇想所要求的连续自然数平方和等式中，第二个的左边是从89963到162540所有36289×2个自然数的平方和，而右边则是从162 541到198 829所有36289个自然数的平方和！用计算机验证一下，两个平方和果然相等，它们都等于1188711884803465。但是，这个解也太大了！

迄今为止我们大部分篇幅都在讨论二次无理数——平方根。我们前面曾指出，所有二次无理数都有周期性的连分数展开式，然而，立方根的情形则非常不同，关于它的连分数至今我们仍然知之甚少。可以说，除了我们以上关于平方根式的介绍，关于连分数的内容大多牵涉到更高深的数学。因此，本章的最后我们只介绍几个趣味性的例子。

大学一年级的数学课一般有一章专门讨论幂级数，在那里，反正切函数的幂级数展开是一个常规的例子，根据欧拉一个关于收敛级数与连分数关系的定理，可以得到：

在x=1的特殊情形，我们得到的左式为正切等于1的角，即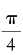，同时将x = 1代入等式右边，则我们最终获得这样一个等式：

作为超越数，π不是任何有理系数代数方程的根，任何有理数的有限次四则运算和整数次幂的乘方开方的值都不可能等于π。然而，它的连分数展开式却是上面这样一个很有规律的形式，这多少有点出人意料。当然，在专家眼里这个展开式并不是“简单”的，因为简单的连分数展开式的所有分子都应等于1。将π写成简单连分数展开可能是可行的，事实上人们得到了关于π的简单连分数展开的许多渐进分数，但是这些分数的分母看起来没有什么规律可循。就π本身而言，它的简单连分数的整数部分是3，而前十几个分母依次是：

7，15，1，292，1，1，1，2，1，3，1，14，2，1，1，2…

就像专家们所说的那样，这些数字里面找不到什么规律，但它们与中国古人对圆周率的分数估计倒是发生了颇为有趣的联系——它的第二个和第四个渐进分数分别是著名的约率和密率：

在本书前面的章节里，自然对数的底数e由已经出现过几次，它有多种不同的定义方式。如果用收敛级数来定义，则我们可以说：

和π一样，e是一个超越数，而不一样的是它的简单连分数展开式是有规律的：

因为连分数展开的这种差别，数学家提出了一个迷人却非常困难的问题：e是否在某种意义上比π要“简单”些？然而，什么叫“某种意义上”？用什么指标来衡量“简单”与“复杂”？或者说，如何用数值来表达数的“复杂度”？这些问题都没有公认标准答案。

圆周率的近似分数

圆周率π是一个超越数，它的连分数没有什么规律可言，但我们可以很容易地计算出其连分数前面的一些分母。除了整数部分等于3外，π前十几个分母依次是：

7，15，1，292，1，1，1，2，1，3，1，14，2，1，1，2，

因此，

1/292是一个很小的数，所以π近似地等于

这，就是祖冲之的密率。一个经常被猜测的问题是：祖冲之究竟是怎么得到这个分数的？

祖冲之密率可能来源

在祖冲之之前，三国时的刘徽已经通过割圆术计算得到3.14和3.1416两个圆周率的近似值。这两个近似值的既约分数形式分别是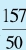和，我们在这里分别称之为“小徽率”和“大徽率”。祖冲之显然知道这两个分数，并且也知道“大徽率”与圆周率非常接近，只是略大了一点点。因此，有一种猜测是：祖冲之通过不定方程寻找比“大徽率”更精确的近似分数，并因此找到密率。这种算法的具体做法如下：

假设是一个比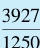小而又非常接近圆周率的分数。由于这个分数比小，故有

因此

3927p-1250q>0。

由于“大徽率”很接近但是略大于圆周率，因此可设

3927p-1250q=1。

用辗转相除法，我们有： 3927=1250×3+177， 1250=177×7+11， 177=11×16+1。于是， 1=177-11×16 =177-（1250-177×7）×16 =177×113-1250×16 =（3927-1250×3）×113-1250×16 =3927×113-1250×355。所以，q和p分别等于355和113。这就是说，密率为。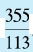

祖冲之密率可能来源之二

由于“小徽率”小于圆周率，而“约率”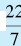大于圆周率，因此，祖冲之可能用“插值”的方法寻找密率。也就是说，他假设n是一个正的整数或分数，使得分数

的值与圆周率非常接近。祖冲之知道圆周率非常接近3. 14159265，于是，他可以列出如下近似等式：

由这个近似等式很容易解得：

很显然，祖冲之应该取n=9，这样他就求得一个圆周率的近似分数，即祖冲之的密率

圆周率的一个简单近似东汉著名学者张衡曾经根据阴阳五行等哲学理论，推出π≈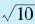的近似公式。这个结果的根据是错误的，近似程度也比当时已知的3.14要差，所以后来招致刘徽的严厉批评。有意思的是，π确实有一个简单的根式近似：

右图中的圆是一个单位圆（即半径等于1的圆），其外是一个外切正六边形，内部则是一个内接正八边形。外切正六边形由六个高等于1的正三角形组成。显然，这些正三角形的边长等于2/ 3，于是，外切正六边形的面积等于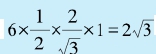。相似地，内接正八边形由八个腰等于1，顶角等于45度的等腰三角形组成。于是，它的面积等于：

单位圆介于内接正六边形与外切正八边形之间，并且我们可以观察到，圆与内接正六边形的面积之差，与外切正八边形与圆的面积之差相差不远。于是，圆面积可以用内接正六边形与外切正八边形面积的平均值来近似。这就是说：

，它并不是一个特别好的圆周率近似值，但这样简单的近似公式，不能不说是一个非常有趣的结果。