数的筛子：证明素数无穷并揭示巨大数之谜

在第三章我们证明过“素数有无穷多个”这个事实。然而，素数虽然有无穷多个，它们出现的频率却呈现出下降的趋势。这个趋势很直观地体现在下列表格中：

解析数论的主要成就之一是证明了描述素数渐近密度的“素数定理”。这个定理说，随着正整数x的增大，小于x的素数之总数越来越接近于x/ lnx。这意味着，对于很大的x，小于x的素数总数的大致的（或者说渐近的）密度为1/ ln x。再换句话说，一个大小与x大致相当的自然数为素数的概率约等于1/ lnx。需要说明的是，这里的对数是自然对数，即以e为底的对数。如果你忘记了，或者从来就没有注意到这种对数，那也不要紧，目前我们只要知道e≈2. 71828就可以了。素数定理说，相继的两个素数之间的差值平均而言将随着x的增大而增加，并给出了增加的大致数值。然而，近年关于孪生素数问题的成果证明，无论x有多大，总存在着比x大但相差小于246的素数对。

无论指定一个多大的数n，人们都可以找到n个连续自然数，使得它们全部都不是素数。举个例子，比如我们想找连续99个合数，那么我们可以取如下99个数：

100！+2，100！+3，100！+4，…，100！+100。

显然这些连续的自然数中的第一个可以被2整除，第二个可以被3整除，其他依此类推。

事实上，上面的取法虽然很容易就得到一个长度为99的无素数数串，但这是非常浪费的做法。我们说“浪费”，意思是完全没有必要到如此巨大的自然数里去找这样的一串数。100！的数值极为巨大，它是一个158位数。素数定理说这个数段中素数之间的平均距离是360，因此在100！之前，一定会有很多很多长度至少为99的素数间距。

由于计算机的出现，亿万个素数已经被计算出来并且存储在磁盘里，目前从网络上可以免费得到前五千万个素数的列表。通过对这些数据的计算机分析，人们获得了一些有趣的统计结果。其中，相邻素数的差以及这些差出现的频率被制作成了表格。第一次出现99个连续合数的时候，其前后的素数分别是396733和396833。它们只是6位数，与158位数相差极远。

话说回来，即便没有计算机的帮助，我们也可以改进做法，在相对小的数里面找到连续99个合数。一个简单的做法是：取Q为100以内所有素数的乘积，即Q = 2×3×5×…×89×97，则Q+2，Q+3，Q+4，…，Q+100连续99个数都是合数。应用常用对数可得lgQ≈36. 36，因此这里得出的99个连续合数都是37位数。换个角度看，我们在37位数里找到了一个大于或等于99的素数间差距。而由于ln 10⁴³≈99. 01，素数定理告诉我们，只有当x大约为44位数时，素数间的平均差距才会达到99。因此，我们这里的结果要优于平均的情形。

由于素数在自然数列的远处非常稀少，因此我们会想：会不会存在所有项均为合数的等差数列？当然，“是”这个答案我们瞬间就可以得到。一个全部为合数的等差数列的例子是

4，6，8，10，12，…，

它的所有项都是2的倍数。事实上，如果我们将等差数列的首项记为a而将公差记为d，则任何a与d不互素的等差数列都具有这样的性质：第二项起就都是合数（假设a与b都是自然数）。因为，如果a与d有公因数，则它也是数列中每一项的因数。

上述问题的反面是一个相对有意义的问题：我们能否找到互素的a和d，使得相应的等差数列中没有素数？答案是否定的。狄利克雷的杰出的成就之一，是证明了一个更强的，以他的名字命名的定理：

每一个首项与公差互素的等差数列都包含有无穷多个素数项。

在18世纪，欧拉证明了所有素数的倒数和是无穷大，也就是说，如果{p_n|n= 1，2，3，…}是所有素数的集合，则和式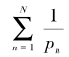

的值当N趋向于无穷的时候的值越来越大，没有任何上界——这种情况我们称级数是“发散”的，它发散到无穷大。狄利克雷引入了一个狄利克雷L-函数，在欧拉成果的基础上证明了上述狄利克雷定理。狄利克雷的贡献后来成为解析数论这个重要的数论分支的里程碑。因为难度较大，我们这本小书不可能介绍狄利克雷的具体证明，但我们可以给出一个表格，来直观地展示狄利克雷的结果：

狄利克雷定理表明，数列{an+d}在a与d互素时包含有无穷多个素数。不仅如此，定理的强化版证明：数列里包含的素数的倒数和趋向于无穷大，也就是发散到无穷大。以表格中的最后一个数列为例，就是

会没有界限地越来越大。

欧拉函数与欧拉定理

如果n是一个正整数，欧拉函数Ø（n）的值就定义为从1到n之间与n互素的整数的个数。例如，对n = 21，由于只有3和7的倍数与21有公因数，因此在1与21之间有

1，2，4，5，8，10，11，13，16，17，19，20

共12个与21互素的整数，因此Ø（21）= 12。

关于欧拉函数，欧拉证明了如下“欧拉定理”：

如果k与n互素，那么

k^Ø（n）mod n=1。

也就是说，k^Ø（n）除以n时的余数等于1。

我们举一个例子来验证：我们取n=21， k=8。此时

k^Ø（n）= 8¹²=68719476736，而68719476736=3272356035×21+1 ，所以，8¹²mod 21=1。

证明上面这个结论当然不是我们在这里可以做到的，但我们可以介绍一个形式上有些相似的级数和发散到无穷的证明。这个级数叫做“调和级数”，它的定义很简单，就是所有自然数的倒数和：

我们把这个表达式的前n项和记为S_n，即

由于每一项都是正数，所以部分和S_n随着n的增加而严格地增加。显然，对每一个大于1的自然数n，都存在一个自然数m，使得2^m≤n<2^m+1。因此，我们有

然而，

以上表达式中共有m-1个方括号，第k个方括号里面有2^k

个项，是从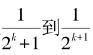

的和。由于这个括号里的每一项都大于或者等于因此，我们有：

这样，整个和式的值就大于或等于

注意，我们说“或等于”的原因是：当n恰好等于2的时候，m的值正好等于1，因此上式中后面的（m-1）个实际上是一个也没有。在这个特别的情形下，级数的部分和与上式恰好是相等的。然而，无论如何我们都证明了这样一件事实：当2^m≤n<2^m+1时，成立着不等式

这证明了级数的部分和S_n趋向于无穷大，因而证明了调和级数发散的事实！

在第三章里我们曾经说，级数

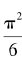收敛于。也就是说，这个级数的部分和以为极限。我们无法在这里证明这个级数收敛于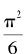这个特别的数值，但我们可以证明这个级数收敛，也就是说，证明它的部分和有极限。我们觉得现在正是介绍这个证明的时机，因为它使用的技巧和上面证明调和级数发散的技巧有很相似的地方。

与前面介绍的证明相似地，我们记这个级数的部分和为S_n，即

很明显，对每一个大于2的自然数n，都存在一个自然数m，使得2^m≤n<2^m+1。由于S_n随着n的增加而增大，所以我们有

然而，

以上表达式中总共有m个方括号，第k个方括号里面有2^k个项，即从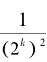到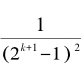的和。由于这个括号里的每一项都小于或者等于，因此，我们有：

这等于是说，整个部分和式S_n的值小于

也就是说，我们证明：当2^m≤n<2^m+1并且n大于2时，

我们知道，以上不等式的右边是等比数列的和，它的值永远小于2。因此，我们证明了：

S_n<2。

也就是说，问题中的级数的部分和是有上界的。由于这个部分和是单调增加的，根据我们以前介绍过的“单调有界原理”，级数的部分和数列是收敛的，因此级数也是收敛的。我们这个证明没有给出级数和的具体值，但它还是提供了有用的信息，它告诉我们：级数和是某个小于2的数值。

解析数论曾经有一个目标是深化素数定理，对小于x的素数之准确总数给出近似公式。一个著名而有用的近似公式记为Li（x），它是一个积分式对给定区间中素数的实际数目，应用这个公式可以得到一个极为接近的近似值。下面所列的是简缩后的相关数据，表中的N是小于x的素数的准确数目。我们看到，虽然所有Li（x）的值都超过准确的N，但这个估计式的相对误差随着x的增大以相当快的速度减小。

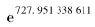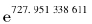我们看到，不仅所有Li（x）的值都超过准确值，这个差值d还随着x的增大而逐渐增大。那么，是不是公式总是估计过头？或者说，Li（ x）是不是从上方逐渐逼近N？从表中看似乎是这样，但这是我们样本太小的结果。英国数学家李特伍德证明差值d不止一次改变符号，随着x趋向于无穷其正负改变无穷多次。那么，d第一次变成负值时的x有多大？答案是未知的，但数学家们一直在研究x的上界。目前最好的上界估计是。也就是说，对某个小于的x值，d的符号会改变。我们知道，的值约为，因此在一般实际应用的范围内，Li（x）几乎总是过分估计了素数的数目。

定积分的例子

本章出现一个定积分，即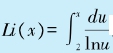。对于没有学过高等数学的读者，我们借这个机会介绍一下定积分的概念。对连续函数f（x），它在区间[a，b]上的定积分记为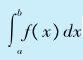。从几何角度看，函数f（x）在[a，b]上与x轴， x=a，x=b三条直线围成一个“曲边梯形”，这个定积分的数值就是这个曲边梯形的（带正负号的）面积。当曲线位于x轴上方时，面积值为正数，反之则为负数。例如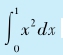，就是如下曲边三角形的面积：

阿基米德的计算方法

阿基米德曾经计算过上述曲边三角形的面积。他的计算方法是这样的：

将[0， 1]区间作n等分，等分点分别是：

如图所示，我们在抛物线下方画出（n-1）个小矩形，由于曲线是y = x²，第k个小矩形的高度等于x_k²=。因此，这些小矩形的面积和就等于

我们知道，前n个自然数的平方和等于，于是，

相似地，图中高出曲线的n个小矩形的面积和等于(www.chuimin.cn)

显然，曲边三角形的面积S满足：S_n<S<T_n。随着n的无限增大，1/ n的极限趋向于0，因而S_n与T_n都趋于。所以，阿基米德说，这个曲边三角形的面积就必然等于1/3。这就是说：

定积分

在第3章我们提到，不存在结果仅为素数的公式。本质上说，寻找素数的唯一办法就是古希腊的厄拉多塞所创设的“筛法”。我们首先写下我们所关心的范围内所有的自然数：1，2，3，4，…。其次，划掉所有我们知道不是素数的数，

剩下来的就是一个素数表。例如，第一步我们保留2，但划去其后所有的偶数；接着，我们干掉除了3之外所有还没有被划掉的3的倍数。现在，我们不需要除掉4的倍数，因为它们在划掉偶数时已经被去掉了。总之，我们的下一步总是从下一个未被划去的数开始，去除它本身之外所有它的倍数。这样，除了5本身以外所有5的倍数就被去掉了，剩下的素数全部都包含在模10的余数为1，3，7，9的数中。我们把尾数为1，3，7，9的这些数列为以上图表，为了节省空间，表中的数只列到100为止，但理论上这个过程可以无限继续下去。表中可以被3整除的数用单线划去，而被7整除的数则用双线。在这个简短的范围内，我们的搜索至此即已完成。剩下的所有数，去掉1然后加上2和5，就是100以内所有的25个素数。我们不需要检查其中是否有可以被11，13等整除的数，这是由于11>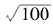，因此如果一个100以内的数可以被11整除，则所得商的数值小于11，因而已经被作为除数检查过。

下面的图表是筛的一种有趣的变体，它对一个数是否为素数可以立刻给出答案。表中的第一行和第一列都是首项a = 4，公差d=3的等差数列。其他行的首项a已经由此给定，对于其公差d，则在第二行用5，第3行用7，其他依此类推。现在，我们有这样一个简单的判别法：

如果x是一个大于2的奇数，则它是素数的充分必要条件是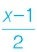不在表中出现。

这个判别定理有各种各样的证明方式，我们介绍其中的一种：令

则

x=2n+1。判别定理说x为合数当且仅当n在上列图表中出现。然而我们真正感兴趣的不是这个图表中的数，而是它们的两倍加一。因此，我们以两倍加一替代表中的每个数，以此构造如下的新图表：

现在，一切看起来就比较明显了。这个表中不包含有任何偶数，其第一行以及第一列包含除3之外所有3的奇数倍，第二行包含的是除5之外所有5的奇数倍，其他依此类推。因此，这个表中列出的恰好是所有奇的合数。

虽然有些数在这个表中出现不止一次，但这个表还是很有效率地略去了所有的偶数——或者说，所有的偶数都被这个筛子筛除。然而我们知道2是唯一的偶素数，因而定理所判别的是除了2之外的所有素数，即所有奇素数。

怎么会这样呢？背后必然隐藏着有趣的数学！确实是的。我们把前后两个图表中的第n行、第k列分别记为 a（n，k）和b（n，k）。显然，在前一个图表中，第一列的通项公式是3n+1。由于第一行的公差为3，此后每行公差增加2，因此第n行的公差为2n+1。这样，由a（n，k）是第n行相应的等差数列的第k项，所以有：

a（n，k）= （3n+1）+（2n+1）（k-1）= 2nk+n+k。

根据后一图表的构造方式，即b（n，k）= 2a（n，k）+1，我们立即得到：

b（n，k）= 4nk+2n+2k+1=（2n+1）（2k+1）。

这就是说，后一图表中的第n行都是2n+1的（大于1的）奇数倍，第k列则都是2k+1的（大于的）奇数倍，因此它包含所有的奇合数！

素数必须在某个针对性的运算过程中被“筛选”出来，它们甚至可以用这种方式来定义，本章的名称正是基于这一事实。我们可以用完全系统化的方式写下所有的合数，上文后一个图表就是一个例子。素数就是剩下的、没有写出来的那部分，这就像是削下肌肉之后剩下的光秃秃的骨头。这个比喻大体上可以说是一个不错的比喻：因为如果没有骨架，那么一个结构就无法站立。而正是素数这种类似“盛宴之后的剩余”的特性，使得数论专家们怀疑：我们是否可以找到一个构建素数的公式？

乌拉姆是美国洛斯阿拉莫斯科学实验室数学部的主任，他带领研究团队使用筛法，发现了一种他们称为“幸运数”的数字集群。用厄拉多塞的筛法时，我们从依次写下“所有”的自然数开始，当然，我们只用前一百个数来作示范。如果我们留下1，然后每隔一个数就划掉一个，则我们去掉所有的偶数而留下如右所示的图表。依厄拉多塞的筛法，我们下一步将划掉所有3的倍数，因为3是下一个存留下来的数。但我们这里的规则不一样：我们现在在留下的数中每三个数划掉一个。这样，5，11，17，23等都被划掉，我们以单条斜线为记号。接下来存留的数字是7，因此我们接着在留下的数中每七个数划掉一个，用两道斜线标记。这样我们就砍掉了19，39等等。然后再每9个数，每13个数地不断进行下去，而相应的斜线数也逐次增加。

这种做法的结果，那些最后存留下来的数被称为“幸运数”。在我们的小于100的短表中，幸运数共有23个，其中10个凑巧是素数，其余的13个是合数。可否整除在这种运算中不起作用，因此运算所得到的结果，或者说“筛选”出来的结果并不都是素数。然而，研究发现，幸运数与素数序列拥有很多共同的渐近性质。例如，它们的渐近密度都是1/ ln N。而在计算机搜索能力的范围内，孪生素数对与孪生幸运数对的个数也展示了惊人的相似性。此外，在计算机可计算的范围内，每一个偶数都可以表示为两个幸运数之和，因此我们可以提出幸运数版本的哥德巴赫猜想。

幸运数拥有那么多被认为是素数独有的性质，这非常令人惊奇，这些发现让一些数学家对素数的看法产生了改变。一些数学家觉得：如果这些性质只是应用筛法的结果，而与是不是素数没有关系，那么素数的一些特有的性质实际上很可能不是独特的。正如上面所说的，传统筛法所“筛选”出来的素数，它的分布规律与幸运数没有什么区别，因此人们会猜测哥德巴赫猜想可以有“幸运数版本”。这，很可能意味着哥德巴赫猜想所蕴含的关于素数的性质其实只是筛法带给素数的某些特质。再推广开来，以哥德巴赫猜想为例，也许我们可以猜测：如果原始版的哥德巴赫猜想成立，那么对自然数以某“合适”的方式实施传统筛法，所筛选出来的数集上相应版本的哥德巴赫猜想也会成立。然而，什么是所谓“合适”的筛选方法？这是一个模糊而深奥的难题。

素数与密码

素数在当代密码技术中有着极为重要的应用。目前最重要的一种加密算法，就是根据素数的性质而发明出来的。这种算法，就是大名鼎鼎的RSA加密算法。

我们说过，人们已经利用计算机计算出了非常多的素数，RSA算法就使用长达数百位的巨大素数。

使用RSA算法加密时，首先要挑选出两个数百位长的巨大素数p和q，然后把它们乘起来，得到一个非常大的自然数n。对这个n进行一系列技术操作，然后用它对信息进行加密。而这些操作的还原，只有在知道p和q的前提下才有可能。

比方说，你的朋友静静想要传送给你一条需要保密的信息。这时，你只需要计算出这样一个n，然后把n传送给静静，并告诉她把信息转化成数字串之后，用n对它加密的办法。她传送出的这条加密后的信息，只有知道p和q的你才能够从中还原出信息的内容。任何其他人，即使截获了这条加密的信息，并且拥有世界上最快的计算机，以及最先进的破解密码的学问，也不可能从中获得丝毫真实的内容。

这种编码方式是革命性的：你可以公开向朋友传送的n以及n的用法，朋友同样可以公开向你传送加密后的信息。它们根本不需要保密，任何获得这些公开的信息的人都无法知道加密信息的内容！

正由于这个原因，这种划时代的加密技术就称为“公开密钥密码术”。

RSA算法

首先找出两个巨大的素数p和q，计算出它们的乘积n=p·q。由于p和q都是素数，在介于1和n之间，只有p和q的倍数与n不是互素的。因此，Ø（n）= （p-1）（q-1）。

接下来，我们还需要找到两个自然数k和l，使它们的乘积等于Ø（n）的整数倍加1。也就是说，它们满足： k·l（mod Ø（n））= 1。

现在，我们手上有p，q，l，k和n则五个数，其中p，q和l需要保密，而k和n则可以向所有人公开。

假设，我们把k和n公开发送给朋友，比如说静静。静静把她要发送的信息转换成数字m，然后计算m^kmod n，将结果记为r，并把它通过公开渠道发送给我们。

收到r之后，我们计算r^l（mod n）。由于r^l=（m^k）^l=m^k·l，而k·l（mod Ø（n））= 1，因此，存在一个整数s，使得k·l=s·Ø（n）+1。于是，

根据欧拉定理，m^Ø（n）（mod n）= 1，我们得到：

就这样，我们利用手中的Ø（n）、l和n，解出了原始信息m！而由于p和q都是巨大的素数，由于大数因数分解的难度，任何人即便知道k和n，也无法计算出解密所需要的Ø（n）和l！

哥德巴赫猜想至今没有得到证明，但我们距离证明它看起来似乎并不遥远。到目前为止，关于哥德巴赫猜想的重要结果大多是应用筛法取得的。当然，数学家们做出了很多筛法的改进，创造了很多高难度系数的技巧。

哥德巴赫猜想在中国极为著名，甚至可以说是公众认为的最重要的数学问题。但是，哥德巴赫猜想也给大众带来几个重要的误解。一个相当普遍的误解是：我们有很多人认为“1+2”等于多少是需要证明的，而有些人甚至说人类到现在都没有证明“1+1”等于几。

由于公众的误解，也由于中国数学家对哥德巴赫猜想问题的杰出贡献，我们有必要在这里对这个猜想的相关知识做一个相对简单的介绍。

首先，简单而通俗地说，哥德巴赫猜想所说的是：

任何一个大于2的偶数，都可以写成两个素数的和。

例如：4 = 2+2； 6 = 3+3； 8 = 3+5； 10 = 3+7；如此等等。这个猜想对相对小的偶数是很容易验证的，在1938年就有人用手工计算验证了10万以内的所有偶数。计算机问世之后，人们开始利用计算机来验证这个猜想，截至2016年，人们已经验证了4×10¹⁸以内的所有偶数，而结果不出意料：所有被验证的数都符合哥德巴赫猜想。

顾名思义，“哥德巴赫猜想”当然是由哥德巴赫首先陈述的，而这个陈述是否正确的问题至今还没有得到解决。克里斯蒂安·哥德巴赫（1690—1764）是德国数学家，他研究的主要方向是数论。他虽然有几个在数论方面可以称为“重要”的工作，但青史留名的原因仅仅是因为他在1742年提出了我们正在谈论的这个猜想。值得一提的是，哥德巴赫本来的专业是法学，在一定意义上他只能算是业余数学家。

哥德巴赫的猜想提出来之后的160多年里，对它的研究没有获得什么重要的结果。然而，1900年希尔伯特在第二届国际数学家大会上提出23个著名的“希尔伯特问题”时，把哥德巴赫猜想纳入了其中的第八个问题，这引起了研究这个猜想的热潮。这个研究热潮持续了数十年，其间大量数学家投身于对这个猜想的研究，发明了“圆法”，并且在传统筛法的基础上创造出许多新的“筛选”技巧。

哥德巴赫猜想说“任何一个大于2的偶数，都可以写成两个素数的和”，对这个猜想的研究在1920年代取得了很多进展，但也遇到了难以逾越的困难。因此，数学家们提出了比原始的哥德巴赫猜想“弱”的命题，他们开始针对给定自然数m和n研究这样的猜想：

任何一个大于2的偶数，都写成这样的两个数之和：第一个数的素因数不超过m个，而第二个数的素因数不超过n个。

研究哥德巴赫猜想的数论专家们为了表达简便，把“一个大于2的偶数”记成“1”，把“一个素因数不超过m的数”记成“m”。基于这样的记号，这个“弱”猜想就可以用符号写成“1=m+n”。也就是说，这个所谓的“等式”的左边代表的是“一个大于2的偶数”，而右边的“m”表示“一个素因数个数不超过m的数”，右边的“n”表示“一个素因数个数不超过n的数”。显然，当m和n都等于1时，这个猜想就等于原始的哥德巴赫猜想。

如果我们知道以上据说的这些符号的真正涵义，我们就不会对相应的“1+2”或者“1 = 1+1”之类的记号产生误解，以讹传讹了。

在上述记号之下，数学家们兵分两路，一路致力于同时降低“m+n”中的m、n两个数，另一路则努力对尽量小的n证明“1+n”，而他们主要的工具恰恰就是筛法。在1920至1960年代，两个方向上的数学家都取得了丰硕的成果，我们将这方面的主要成果列表如下：

从以上表格中我们看到，中国数学家对哥德巴赫猜想的研究工作非常出色，其中陈景润证明了至今最好的结果。但我们再一次提醒读者们注意，按照我们先前的介绍，所谓“1+2”，也就是陈景润所证明的结论，它的真正意义是：

任何一个大于2的偶数，都写成这样的两个数之和：第一个数是素数，而第二个数的素因数不超过2个。

在这个结论中，“素因数不超过两个”当然就是“要么恰好有两个素因数，要么就是素数”的意思，如果有人可以把“两个素因数”这种可能性排除掉，那么哥德巴赫猜想也就得到了证明。从这个意义上说，陈景润的结果距离解决哥德巴赫猜想“只有一步之遥”。然而，时间过去了四五十年，陈景润去世也已经20多年，数学界却没有能够跨越这一步。不少数学家认为，陈景润已经把筛法用到登峰造极的地步，不开发出新的工具的话，解决这个猜想可能遥遥无期。

最后，我们想在这里提醒所有的数学爱好者：哥德巴赫猜想经过全世界数以百计的顶尖数学家的长期钻研，至今仍然没有完全解决。在当前知识范围内，所有解决猜想的可能方法都已经被仔细而反复地推敲过。因此，如果没有至少数学专业研究生以上的正规教育，仅凭热情和雄心，解决这个猜想是不可能的。我们希望，所有有雄心想要解决这个难题的数学爱好者们，在成为数学专家之前不要在这个问题上浪费青春。

希尔伯特

大卫·希尔伯特（1862—1943）是德国著名数学家，作为哥廷根学派的领袖，希尔伯特是19世纪末至20世纪初全球数学界的旗帜，被誉为“数学界的无冕之王”。希尔伯特的研究范围十分广泛，他在不变量理论、代数数域理论、积分方程、一般数学基础等领域中都做出了重大甚至开创性的贡献。

在1900年巴黎第二届国际数学家大会上，希尔伯特发表了题为《数学问题》的著名讲演，提出了23个最重要的数学问题，即所谓的“希尔伯特问题”。这些问题的提出，在此后的100年间积极推动了数学的发展。在所有23个希尔伯特问题中，至今已有10个问题获得圆满解决，有7个得到部分解决，有2个因含义不清而未被深入研究，此外的3个数学问题及1个物理问题至今悬而未决。

希尔伯特相信科学的力量，他曾在一次演讲中发出这样的豪言：“我们必须知道，我们必将知道。”后来，这句话就刻在了他的墓碑上。