数字的神奇之旅：完美平方与逆序数

数学爱好者们发现了很多关于数字的神奇现象，这一章我们向大家介绍的是其中特别有趣的一小部分。我们将会兼顾数学与趣味，有的仅仅介绍趣味的等式或现象，有的则会给出一些分析和证明。我们先来看看以下一组等式：

12²=144， 21²=441

13²=169， 31²=961

102²=10404，201²=40401

103²=10609，301²=90601

112²=12544，211²=44521

113²=12769，311²=96721

122²=14884，221²=48841

发现这些等式的奇特之处了吗？是的，以上每一行两个等式的左边都是相互逆序的两个自然数的平方，而右边的值恰好也是相互逆序的！这种数对没有公认的名称，我们这里暂且将它称为（一对）“平方逆序数”。那么，这样的“平方逆序数”有多少？我们又怎么找出它们呢？这是个好问题。

我们下面只对其平方为三位数的两位数略加分析。我们考虑的是十进制数，所以我们事先声明：所有数位上的字母表示的都是1到9之间的某个数字。现在，我们假设有一个两位数10a+b，它的平方是三位数100c+10d+e。不仅如此，它的逆序两位数10b+a的平方恰好等于100e+10d+c。也就是说，我们有：

（10a+b）²=100a²+20ab+b²=100c+10d+e，

（10b+a）²=100b²+20ab+a²=100e+10d+c。

由于前一式的右边是一个三位数，因此a²不超过9，也就是说a²没有产生进位。同理，b²也没有产生进位。这样，我们就发现：a²=c，b²= e。这导致另一个条件必须成立：20ab也不能进位。因此，我们推导出的条件是：

a≤3，b≤3，a×b<5。

考虑a≤b的情形，则符合以上三个条件的（a，b）组合总共有：（1，1）、（1，2）、（1，3）以及（2，2）四个。

通过以上推导我们发现，除了12和13以外，11和22也是平方逆序数。由于11和22本身就是自己的逆序，于是我们立刻知道它们的平方数也是自己的逆序数，也就是左右对称的数字。

很显然，进位制不同的时候，数的表示也不同，因此“平方逆序”的情况也不一样。这时背后有些什么有趣的现象？我们没有展开研究，但可以举一个例子：9在八进制中写成11，它的平方的八进制写法是121，这和十进制中11²= 121形式上是一样的。

两位数的平方可以是四位数，这些数中没有一个满足上述这种神奇的逆序形式，但是其中有一对数也相当神奇：

33²=1089，99²=9801。

虽然四位的完全平方数没有对应的平方逆序数，它们中却另有别样的神奇：其中有连续五个四位平方数，它们的前半部分组成的两位数与后半部分组成的两位数的和也是完全平方数！也就是说，我们有如下一组神奇的等式：

86²=7396， 73+96=169，169= 13²

87²=7569， 75+69=144， 144= 12²

88²=7744，77+44=121，121= 11²

89²=7921，79+21=100，100= 10²

90²=8100， 81+00=081，081= 09²

为叙述方便，我们把上述那种“前半部分与后半部分相加”的运算称为“折半和”运算。那么，我们的问题又来了——对大于2的正整数n，有没有一长串连续的n位数，使得它们平方的“折半和”都是完全平方数？答案是肯定的，接下来，我们在增添一个附加条件的情况下作答——

（05） x+y=10ⁿ-1。

问题：x是什么数？

以上假设中，（01）是说x为n位数，（03）是说K和L就是把x²折成两半所得的两个数，（04）是说“折半和”恰好是完全平方数。

很容易证明：在n>2时，（02）式在（01）成立时自动成立。因此，我们所要求的就是满足（01）、（03）、（04）以及（05）这四个条件的自然数。假设（05）就是我们增添的附加条件，这条额外添加的假设，是我们得到以下解答的关键。

解答的过程有些长，但我们认为如此详细的介绍是值得的，拿起笔跟着演算的读者会有额外的收获。首先，从（05）出发，我们有

y²=（10ⁿ-1-x）²=（10ⁿ-1）²-2（10ⁿ-1）x+x²。

据（04）、（03）以及上式，则有

K+L =（10ⁿ-1）²-2（10ⁿ-1）x+x²

=（10ⁿ-1）²-2（10ⁿ-1）x+10ⁿK+L。

移项、整理，容易得到

（06） K=2x-（10ⁿ-1）。

由于x是一个n位数，我们取一个实数r，使得

当然，这里的r未必是有理数，更未必是自然数，但由（01）我们可以知道

（08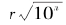）是自然数。用floor（x）表示不超过x的最大整数，则据（03）式，我们有

也即是说，K是x²除以10ⁿ所得的整数部分。

由（07）式，我们得到

根据（08）式，则有

因此，再由（06）和（07）式，我们推出

即

综合（09）、（10）、（11）式，不难发现

（12） floor（r²）= 1。

这就是说，r虽然未必是有理数，但是r²的整数部分必定等于1。

从以上推演中我们可以发现：由（07）式表示的x满足（01）-（05）的充分必要条件是（12）。也就是说，只要r满足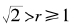，则（07）式表示的x就是我们要求的。因此，问题的解答是：

以x为三位数时作例子，我们有≈31. 62，因此所求的三位数开始于1000-44= 956，而最后一个数则是968，整个连续自然数串的长度为13个。为避免烦琐，我们仅列出首尾两个数的相应运算：

956²=913936，913+936=1849，1849=43²。

968²=937024，937+024=961，961=31²。

除了以上所得到的长串连续自然数之外，还有其他一些折半和为完全平方的自然数。它们有些是零星的，有些形成很短的连续串。典型的短串是由两个数组成的，最小的一组是49和50：

49²=2401，24+01=25。

50²=2500，25+00=25。

很容易证明，对所有正整数k，5×10^2k-1-1和5×10^2k-1都构成一个短串。

趣味数字：666

以前有一种剧毒农药叫作“六六六”，因为环保问题，这种农药已经被禁用。有趣的是，传统的基督教教义认为，666是一个邪恶的数。这是因为，据《圣经·启示录》，13章第18节，666是“野兽之数”：

“在这里有智慧。凡有聪明的，可以算计兽的数目。因为这是人的数目，他的数目是六百六十六。”

这个数有一些特别的有趣之处，它是前七个素数的平方和：

666=2²+3²+5²+7²+11²+13²+17²

又是前六个自然数的“回旋立方和”：

666=1³+2³+3³+4³+5³+6³+5³+4³+3³+2³+1³

由于666是一个“邪恶的数”，有些人就会将它作为某个人是“邪恶的人”的证据。最著名的一个例子是关于比尔·盖茨。不少人讨厌这位世界首富，于是就想办法寻找他的与666的联系。由于盖茨的全名是“威廉·亨利·盖茨三世”，这些人就用“BILLGATES3”来对应数字。在计算机中，最常用的一套字母的码值叫作ASCII码。从A到Z这26个字母的码值是从65到90连续26个自然数，因而“BILLGATES3”就对应了66，73，76，76，71，65， 84，69，83，3，而这十个数的和恰好就是666！

当然，上述“巧合”是精心寻觅的结果，绝不证明盖茨是“坏人”。试想，“3”作为字符也有它的ASCII值，为什么不用它的ASCII值而直接用数字3？盖茨名字中的“亨利”又哪里去了？事实上，盖茨是全世界最大的慈善家，这种编排他的做法是很不公道的。我们引述这个例子，一方面是提供一个关于666的趣味例子，另一方面也是想借此批判“数字神秘主义”。

趣味数字：495

随便找一个三位数字不全相同的三位数，用它的三位数字从大到小排列构造一个新的三位数，再从小到大排列也构造一个三位数。将新构造的两个三位数相减，得到一个三位数。然后，对得到的结果重复以上“构造-相减”的步骤……如此数次，最后总会得到同一个数：495！

例如，我们选择三位数729，依上述构造法，首先得到972和279，二数相减，得到693。对693，依法得到963和369，相减得到594。对594，我们得到954和459，它们相减就得到495。

上面我们考虑的是一串连续自然数，如果我们放宽条件，转而考虑公差为某个大于1的自然数的数列，则又会提出一个特别有趣的问题。在公差为3，9，11，30，100，300等数时，我们都可以找到平方折半和等于完全平方的数串。例如，在公差等于3的时候，三位数里有多个长度至少为4的串，最长的一串有7个数：

348²=121104，121+104=225=15²；

351²=123201，123+201=324=18²；

354²=125316，125+316=441=21²；

357²=127449，127+449=576=24²；

360²=129600，129+600=729=27²；

363²=131769，131+769=900=30²；

366²=133956，133+956=1089=33²。

有意思的是，在公差等于300的四位数自然数列里，有一个长度达到23的长串，它们的统一表达式是：

3267+300·k，0≤k≤22。

对所有这些数，我们有：

（3267+300·k）²

=10673289+1960200k+90000k²

=10000·（1067+196k+9k²）+（3289+200k）

容易验证，（1067+196k+9k²）和（3289+200k）当0≤k≤22时都是四位数，而对上述平方折半求和，则有

这就是说，3267+300·k的平方折半和等于66+3k的平方！如果我们放宽一点，将平方只有七位数的情况当作首位为0的八位数，那么这个数串可以延伸到k = -7时，整个串的长度总共达到30。在k=-7时，1167²=01361189，它的对折和同样符合以上公式，等于45的平方。

据说以前北京有一座寺院叫作“大佛寺”，有人游览后在墙上写下了“人过大佛寺，寺佛大过人”十个字。后来有人秋游黄山，留下了“黄山落叶松叶落山黄”的即景题句。这两句话顺着念和倒着念是一样的，也就是说，它与自己的逆序相同。这样的文句，修辞学中的术语称为“回文”。

前文我们提到11²= 121，22²= 484，且11，121，22，484四个数都和它们自己的逆序相同，所以我们借用修辞术语，称这种数为“回文数”。

如果一个自然数是回文数，而且它的平方同时也是回文数，我们称它为“双回文数”。两位数中只有11和22两个双回文数，而三位数中则有五个：

101²=10201，111²=12321，121²=14641， 202²=40804，212²=44944。

四位数中的双回文数反而比三位数少，只有1001，1111和2 002三个。不过，五位的双回文数又多了一些，共有10001， 10101，10201，11011，11111，11211，20002，20102八个。

对照以上列出的双回文数，我们不难发现其中的规律。相似地，自然数本身及其立方都是回文数的情况也存在，但更加稀少，大于10而小于10 000的这种数只有11，101， 111，1001四个，而它们其实也是本身、平方、立方“三回文”的。

此外，也许在一些读者看来，自然数本身不是回文数，但它们的平方或者立方是回文数的情形也是有趣的。这种数也很稀有，我们下面列出其中的几个：

几种趣味素数

（1）回文素数。两位的回文素数只有一个：11。三位的回文素数有14个，即101，131，151，181，191，313， 353，373，383，727，757，787，797和919。五位的回文素数有10301，10501，10601，11311，11411，12421，12721，12 821，以及13331等。

（2）绕转素数。3779是一个素数，把它的首位数字“绕转”到后面，得到的7793也是一个素数。7793再绕转一次，所得到的7937也是素数。同样，9377也是素数。在趣味数学中，我们把所有“绕转”都是素数的数称为“绕转素数”。四位的绕转素数有1193，3779以及它们的所有绕转。五位和六位的自然数中，11939，19937，以及193 939也是绕转素数。

（3）全一素数。各位数字都等于1的数称为“全一数”，全一数中的素数称为“全一素数”。11是最小的全一素数，此后的两个全一素数分别是1111 111111 111 111 111和11111 111111 111111 111111，分别有19个和23个“1”。而再接下来的两个全一素数所含的“1”非常之多，分别含有317个和1031个。

（4）重排素数。如果一个数的所有重排都是素数，那么它就称为“重排素数”。三位的重排素数有113，199，337，以及它们的所有重排。事实上，它们恰好就是所有的三位绕转素数。人们猜测，四位以上的重排素数只有“全一素数”。

大家熟知的六位数142857显然是一个具有奇趣的数字，将它分别乘以2，3，4，5，6时，得数总是原来六个数字的一个循环排列。然而我们在第5章分析过它的这种特性，提示了这种特性产生的原因，并将它与1/7的循环节联系起来。略有些相似地，1/81的循环节也向我们呈现一幕神奇的数字景观。

1/81的循环节是“012345679”。因为这个循环节有九位，所以我们暂时放宽“九位数”的定义，把这种以“0”开头的八位数也算作九位数。我们注意到，012345679这个数里面，十个数字唯独缺了一个“8”。现在，我们将十个数字只缺一个的九位数称为“独缺数”。那么，神奇的现象出现了：对任何一个小于81的自然数k，如果它不是3的倍数，则它与012 345679的乘积也将是一个独缺数！

关于012345679乘积的独缺数现象显然是非常神奇的，但是它有一个不足之处：不是所有小于80的数与它的乘积都是独缺数，每隔三个就会跳开一个。产生这种现象的原因在于9不是素数。事实上，在n进制中， 1 / （n-1）²的循环节的性质与012345679是相似的。而如果n-1是素数，则该循环节与所有小于（n-1）²，但不能整除n-1的自然数之乘积都会是n进制表示下的独缺数。也就是说，1 /7²在八进制中是一个无限循环小数，其循环节的独缺数性质更漂亮，它每隔六个才跳开一个。

我们现在开始暂时来使用八进制。首先一个问题，十进制的49在八进制中应该写成什么样子？我们借用习惯的十进制来思考：49= 48+1，48是8的6倍。因此，按照八进制“逢八进一”的进位规则，十进制的49在八进制中表示为61，即6个8¹加上1个8⁰。

我们再熟悉一下八进制，先引入八进制的加法表和乘法表，然后来计算八进制中的123 457乘以13的结果。

根据以上乘法表和加法表，我们把进位写在右上角，则有

因此，在八进制中，13×0123457= 1627405。这里的0123457正是八进制中的1/7²的循环节。为展示八进制数0123457的独缺数性质，我们下面列出它与八进制中的10至15、35至42两段共12个数的乘积。我们希望读者能发现其中的一些奥妙，例如：所缺数字与乘数的关系，两个表中对应位置的乘积值的关系等等。

有一个流传很广的段子，说老师在点名时把名叫“朱月坡”的同学叫成了“朱肚皮”，引起全班的哄堂大笑。古人也有一个段子，说有人把“己亥渡河”误抄成了“三豕渡河”，硬是把一个军队越境的事件错误地写成了一场猪的游泳比赛。这两个故事说明：手写确实比较容易产生误解。

数学界也有一个段子，说有人把数字依次为a，b，c，d的一个四位数抄成了a^bc^d，却很凑巧地得到与原来的数字相等的数值。那么，这个有趣的数是什么呢？换句话说，等式(www.chuimin.cn)

a^b×c^d=1000a+100b+10c+d，

在a，b，c，d都是1到9之间数字的前提下，有什么样的解呢？答案只有一个：

2⁵×9²=2592。

验证这个答案的正确性是很容易的，证明它的唯一性有两种方法：一种是穷举，我们可以编一段小程序，每个数字只有9种选择，因此只要计算9⁴种可能性，就可以验证答案的唯一性。另一种则是用分析讨论的方法，这是锻炼思考分析能力的好办法，在没有计算机的时代也是比穷举更有效率的做法。

对这个问题完整的分析讨论相当繁复，不适合在这里介绍，我们来考虑一个简化的问题——在已经知道这个数的首尾数字都等于2时，如何来确定中间两个数字的问题。此时，我们的等式是

2^b×c²=2000+100b+10c+2。

首先，c²小于10的平方，即小于100。但是它与2^b的乘积是一个大于2000的数值.因此，2^b必须大于20。这样我们得到第一个结论：

（1） b≥5。

其次，c²的尾数只能是1，4，5，6，9。由于b从5到9时2^b的尾数依次是2，4，8，6，2。由于右边尾数为2，而6乘以1，4，5，6，9所得的尾数不可能等于2，因此b只能是5，7，8， 9中的一个。而如果b= 9，则2^b尾数为2，这要求c= 9。但是右式小于3000，它除以2⁹的结果小于6，所以b= 9也不可能。因此，我们可以进一步缩小b的范围，得到

（2） b=5或b=7或b=8。

现在，我们考虑b=7的可能性。如果b=7，则等式右边的数值在2 700与2 800之间，除以2^b的得数在21至22之间，不可能是一个完全平方数。因此，b= 7是不可能的。同样的道理，b=8时右边除以2^b的得数在10至12之间，也不可能是完全平方。这样，我们就有

（3） b=5。

于是，根据尾数关系，我们马上得到c= 9。因此本问题的答案即是：

2⁵×9²=25×81=2592。

抄错或看错有时会产生可笑的错误或有趣的巧合，错误的运算有时也会凑巧得到正确的结果。笔者中学时曾经在一道证明题中两次使用“圆幂定理”的错误形式，然后“证明”了问题的结论。那次“一时糊涂”我至今不忘，因为它让我丢掉本该到手的一枚竞赛金牌。

相比于圆幂定理，下述错误的“约分”要低级得多，但结果却凑巧是正确的：

那么，还有没有其他分子、分母都是两位数的分数，可以如此错误地“约分”呢？有一种“平凡”的情形是显然的，它形如

对一般情形，这个问题其实是要求解

将上式去分母并整理，我们得到

9xz=y（10x-z）。

因此，如果9整除（10x-z），则有

10x-z≡0（mod 9），

10x≡z（mod 9）。

而由于

10≡1（mod 9），

所以

10x≡x（mod 9）

对所有x成立。由于x与z都只有一位数字，因此可得x=z对所有x成立。这，就是我们指出的平凡的情形。

考虑非平凡的情形，则这时9不能整除（10x-z），因此3必然是y的一个因数。这样，我们就缩小了搜索目标分数的范围。略加尝试可以找到所有其他满足条件的分数，它们是：

分子和分母的位数更多的情形讨论起来没有那么容易，但是计算机编程来寻找的话，一天可以找出几万个，笔者写了十多分钟的代码，执行了几秒钟就找到了3000多个——下面随机列出其中的三个：

我们在第2章曾经提到过完全数，最小的几个完全数依次是：

6，28，496，8128，33550336，8589869056。

很久以前人们就知道，对第一个之外其他任何完全数，把它的各位数字相加得到一个新数，再将此数各位数字相加，如此反复进行，则最终得到的数字一定是1。以8128为例， 8+1+2+8=19， 1+9=10，1+0=1。

现在，我们在完全数这一种趣味数字里又发现另一件趣事。但我们有两个问题：首先，为什么反复将各位数字相加最终得到的会是1？更有趣的是，为什么这个规律对第一个完全数会失效？幸运的是，答案其实并不复杂。

回顾一下我们在第2章所证明的结果——所有偶完全数都是形如2^p-1（2^p-1）的数，其中p是素数。所有的素数中除了2之外都是奇数，因而我们暂且认定p-1是偶数。这样，由于

2≡-1（mod 3），

我们得到

2^p-1≡1（mod 3）。

这就是说，存在正整数k，使得2^p-1=3k+1。乘以2则得到

2^p=6k+2， 2^p-1=6k+1。

因此，

2^p-1（2^p-1）= （3k+1）（6k+1）= 18k²+9k+1≡1（mod 9）

这就是说 2^p-1（2^p-1）-1≡0（mod 9）。

回顾本书第2章中的内容，我们知道对任何被9整除的数，反复求各位数字之和的结果等于9。因此，在减去1之前，我们的完全数各位数字反复求和所得数字为10，这就完成了我们的证明。

问题来了——为什么这个规律对6这个完全数失效？原因是：并非所有的素数都是奇数。我们p-1是偶数的断言当p为2的时候是错误的，而这时对应的完全数恰好就是6，所以6这个完全数恰好不在上面论证的范围之内。

各位数字的平方和

任意取一个自然数，将它的各位数字的平方加在一起，得到一个自然数。对得到的结果，再次进行“取各位数字平方和”运算……如此不断进行下去，最后会得到什么结果呢？

很有意思的是，对大约14%的自然数来说，最后的结果会是1！那么，其他的数呢？对所有其他的自然数，不断进行“取各位数字平方和”运算得到的结果是一个数字循环：

4→16→37→58→89→145→42→20→4

例如：考虑自然数1728，它的各位数字的平方和等于1+49+4+64=118，118和各位数字平方和是1+1+64= 66， 66的各位数字平方和等于36+36= 72，接下来“取各位数字平方和”的结果依次是53，34，25，29，85，89，145，42， 20，4，16，37，58，89，…，陷入上述循环。

再举个例子，对自然数999998，它的各位数字平方和等于81*5+64 = 469，此后“取各位数字平方和”依次是133，19，82，68，100，1，…，最终一直停留在1。

上面我们对完全数做了不断重复地“将其各位数字相加”的运算，与此类似的一种运算是：对一个自然数，将其各位数字求立方和，然后对计算出的结果不断重复这种运算。那么，我们新引入的这种运算会得到什么结果呢？答案是非常有趣的：对所有的自然数，不断重复求各位数字立方和的运算得到的结果分为两种——一种是最终得到一个固定不变的数，另一种是最终落入几个数的循环。其中，固定数总共有五个：

1，153，370，371，407。

循环总共有四个，其中两个的周期是2，另两个的周期是3：

136*244，919*1459；

上述运算最终得到固定数或循环圈的现象当然是很有趣的，其实固定数和循环圈本身就展示了自己的奇妙之处，例如，我们从中得到：

3³+7³+1³=27+343+1=371；

9³+1³+9³=1459，1³+4³+5³+9³=919。

读者可能会有两个疑问：一是以上这个结果该怎么证明？二是我们为什么不考虑数字的平方和而考虑立方和？后一个问题其实比较容易解释，因为考虑数字平方和时，固定数只有1这样一个“平凡”的数字。而前一个问题其实也不复杂，我们的推证方法可以概括为两点：（1）证明大的自然数的各位数字立方和比它自身要小，因此经过反复运算后所有结果都会小于某个数M（比如M可以取为 3000）；（2）对小于M的所有自然数进行反复运算，求得最终结果。需要指出的是，第（2）点在学会计算机编程后是很容易的，可以说，编程是寻找数字中奇妙性质的得力帮手。

尽管方程p²/ q²=2没有整数解，但方程

的解则很容易找到。例如

如果要求平方和中的数是连续的自然数，我们也可以找到这样珍奇的等式：

甚至还有更加让人惊讶的等式：

事实上，所有从（10k+1）到（10k+7）的自然数平方和，从（10k+3）到（10k+9）的自然数平方和，都是从1到7的平方和的整数倍！

在立方和中也可以找到相似的等式，通过计算机我们可以很快找到例子，例如：

然而，更神奇的事情还藏在后面，从2到10这9个连续自然数的立方和看起来相当特殊，因为有无穷多种连续9个自然数的立方和是它的倍数！仔细的计算证明，当k为非负整数，而n=14k+2，n=14k+4，或n= 14k+10时，从n到n+8这9个自然数的立方和都是从2到10的立方和的整数倍，三种倍数依次是如下k的表达式：

这些公式有些抽象，但表格是非常直观的，我们计算出上列公式中的前6个，列表如下：

关于立方和还有很多类似的现象，而关于平方和的类似情况，则应该更多并且公式更简单，但我们决定到此为止，意犹未尽的读者可以自己展开探索。

四平方和恒等式

在公元六世纪，古印度人发现两个平方和的乘积也可以写成平方和的形式，这就是著名的“婆罗门笈多恒等式”：

1000多年之后，伟大的欧拉发现了一个相似但更复杂的等式——两个四平方和的乘积也是四平方和：

这个称为“四平方和恒等式”的公式，后来成为拉格朗日和欧拉证明“四平方和定理”的重要工具。

关于四平方和定理

四平方和定理告诉我们：每个自然数都可以写成四个整数的平方和。而事实上，有些自然数可以写成一个、两个、或三个自然数的平方和，有些则必须写成四个自然数的平方和。具体地说，我们有如下有趣的结果：

（1）如果a和k都是非负整数，而自然数m可以写成m=4^a·（8k+7），则m不能写成三个整数的平方和。

（2）如果a和k都是非负整数，而自然数m可以写成m=4^a·（8k+l），其中l为1，2，3，5，6中的一个，则m可以写成三个整数的平方和。

（3）如果m是形如4k+1的素数，则它可以唯一地写成两个自然数的平方和。需要说明的是，这种素数大多也可以写成三个或四个自然数的平方和。例如，61有唯一的二平方和形式，即61 = 36+25。同时，它也可以写成三平方和及四平方和形式：61=36+16+9，61= 49+4+4+4=25+16+16+4。

（4）如果m是两个或多个形如4k+ 1的不同素数的乘积，那么它可以写成（多种）两个自然数的平方和。

考虑在以下图中展示的规律：

图中的第一个关系并不难证明：式子的左边是从n²到n（n+1）的所有n+1个连续自然数，右边则是从n（n+1）+1到n（n+1） +n的所有n个自然数。按等差数列的求和公式，左边之和应为

我们很容易证明右边的和也有同样的表达式，因此，以上图形中的等式都无疑是正确的。然而这里还有一个有趣的看点：这个和式恰好是从1到n的平方和的3倍！

第二个关系式左边是从（2n²+n）到（2n²+2n）之间所有n+1个连续自然数的平方和，右边是从（2n²+2n+1）到（2n²+3n）之间所有n个连续自然数的平方和。为了证明左右两式相等，我们来计算右边减去左边的后n个平方和，它等于k从1到n时所有n个形如（2n²+2n+k）²-（2n²+n+k）²[]的项之总和，我们把它记为：

利用平方差公式，我们可以将上述和式的通项可以化简成n（4n²+3n+2k），因此，这个和化为：

上式后一部分中的和式是从1到n时所有自然数之和，我们知道它等于n（n+1） /2，因此，整个式子就等于

n（4n²+3n）·n+2n·n（n+1） /2，

整理得到（2n²+n）²，这恰恰就是原来的左边移去后n个平方和之后剩余的那一项！

上述两个等式列表成立的原因惊人地相似，其紧靠等式右边的那个数字都是它们的关键。在第一个列表中，这个数依次是2，6，12，20，…，它们是表达式n（n+1）在n= 1， 2，3，4，…时的值。在第二个列表中，相应的数是4，12，24， 40，…，正好是n（n+1）的两倍。在第n个等式中，左边是（n+1）个连续整数而右边则是n个。当然，两个系列的通项是不一样的，前一系列等式的两边正好穷尽所有的自然数，而后一个则不然。

看到上述两个列表的这种相似，我们自然会猜测说这种情形还可能继续下去，但事实并非如此。下一个列表中间的数应该是[3n（n+1）]³，但是我们知道这不可能——因为，第一个等式应该是5³+6³= 7³，而费马大定理告诉我们这是不可能的。略微显得有趣的是，这个式子虽然不成立，但它差一点点就成立了，因为7³= 343，而

5³+6³= 341，两数相差的数值仅仅为2。

由于上述两个系列的等式非常有趣，于是我们尝试寻找相似的系列等式。对连续非负整数和的情形，很多不同的限制条件下都可以得到有趣的等式。例如，要求右边和式的项数比左边少2，则有：

很容易证明，以上系列的第n行左边最靠近等号的项为2n²，左边共有2n+1项，而右边则有2n-1项。同样有趣的是，这系列等式恰好穷尽所有的非负整数！最后要强调一下，我们这里仅举出一个例子，而事实上很多其他限制条件也会导致有趣的等式系列，我们把它们留给意犹未尽的读者来挖掘。

寻找性质相似的连续平方和等式系列的难度较大，我们不作深入的讨论。但我们通过计算机编程寻找，也发现了若干有趣的关于连续自然数平方和的等式，下面我们列举几个，也许读者在赏玩之余能从中发现某种规律。

尤里卡定理

我们在第二章提到，三角形数是形如n·（n+1） /2的自然数。高斯在他1796年的日记里写道：“尤里卡！ num=△+△+△”。这是说，他证明了这样一个定理：每个自然数都可以写成三个三角形数之和。

四边形数就是完全平方数，因此，四平方和定理告诉我们，每个自然数都可以写成四个四边形数之和。

更一般地，费马在1638年不加证明地提出所谓的“费马多边形数定理”，即“每个自然数都可以写成n个n边形数之和。”拉格朗日在1770年证明了n = 4的情形（即四平方和定理），高斯在1796年证明了n= 3的情形，而柯西在1813年完整地证明了费马多边形数定理。

我们以n=19为例。首先，三角形数的公式是n·（n+1） /2，而五边形数的公式则是n·（3n-1） /2。因此，0， 1，3，6，10等是三角形数，而0，1，5，12，22等则是五边形数。对n=19，显然：

19=10+6+3，是三个三角形数之和，

19=16+1+1+1=9+9+1+0，是四个四边形数之和，

19=12+5+1+1+0，是五个五边形数之和。

上文中我们看到了很多自然数的平方和等式，而古人则对任意自然数的平方和表示问题非常感兴趣。在1770年代，拉格朗日和欧拉先后独立地证明了这样一个定理：任何一个自然数都可以表示成四个整数的平方和。由于拉格朗日早一年发现这个定理，因此它被称为“拉格朗日四平方和定理”。需要注意的是，这里所说的“四个整数”中，有可能含有若干个0。

这个定理显然是很有趣的，而更有意思的是，有些自然数可以表示成很多很多种不同的“四平方和”形式，而有些却只有一种表示方式。不难证明，所有2的奇数次方都只有一种四平方和表示，即

2^2n-1= （2^n-1）²+ （2^n-1）²+0²+0²。

而计算机验证表明，自然数1554总共有85种不同的四平方和表示，9450的四平方和表示方式则达到惊人的664种！作为例子，下面我们列出1554的24种不同的四平方和表示，至于1554的其他61个四平方和表示式，有兴趣的读者可以编写一段计算机程序来寻找。