丢番图方程解析：破解整系数代数方程，取得惊人成果

亚历山大的丢番图是古代西方最著名的数学家之一，他大致生活于公元3世纪，相当于我国的三国到西晋时期。丢番图致力于研究简单代数方程的求解问题，并且取得很了不起的成果。在现代数学里，丢番图方程所指的是考虑整数解时的整系数代数方程。

上一章我们提到一个丢番图方程：x²-3y²=1。这个方程有无穷多个（正整数）解。我们证明，这些解从小到大排成一个列{（x_n，y_n） |n=0，1，2，…}，则商的数列{x_n/ y_n}以3为极限。

现在考虑一个相似的丢番图方程：x²-3y²=2，我们来证明它没有正整数解。

首先，如果（x，y）是这个方程的解，那么由于方程的右边等于2，所以x和y的奇偶性是相同的。假如x和y都是偶数，则方程左边是4的整数倍，而右边则等于2，这显然是不可能的。因此x和y不可能都是偶数。如果有解，x和y必须都是奇数。

现在考察x和y都是奇数的情形，即假设

x=2m+1，y=2n+1。

将这两个表达式代入方程，则有

（2m+1）²-3（2n+1）²=2，

展开平方，并移项整理，得到

4[m（m+1）-3n（n+1）-1] =0。

连续自然数m和m+1中必然有一个偶数，因此上式左边的方括号里前两项都是偶数。而由于最后一项是奇数1，因此左边的表达式不可能等于零。这就是说，等式不可能成立，或者说，x和y不可能都是奇数。这样，我们就证明了x²-3y²= 2不存在（正整数）解。应该指出：这个证明的关键是关于4的整除与余数问题，如果应用第4章的同余算术来表述，这个证明就会简洁得多。我们有意采用更初等的方式，把应用同余算术的表述留给读者完成。用与前述证明相似的方法，我们可以证明丢番图方程

x²-3y²=2z²

也没有（正整数）解。而这个结果其实表明，方程x²-3y²= 2不仅没有正整数解，而且也不存在有理数解！

我们看到，有些丢番图方程没有（整数）解，而有的则有无穷多组解。对一个丢番图方程，“找出所有解”的意思是找出能系统性地得到所有解的公式或者步骤。

上一章我们指出，我们当时列出的递推公式其实给出了方程x²-3y²= 1的所有解。也就是说，我们已经找出了这个丢番图方程的所有解。这一事实的证明思路是这样的：如果（x，y）是方程x²-3y²=1的一组比（2，1）大的解，则不难验证（2x-3y，2y-x）是一组比（x，y）小的解。因此，从方程的任何一组解出发，我们可以一直下推，直到得出无法再小的一个“最小（正整数）”解。然后我们证明，这个无法再下推的“最小”解必定就是我们递推公式的第一组解，即（2，1）。

丢番图与丢番图方程

丢番图生活在罗马帝国的亚力山大港，他是第一个将符号引入代数学的数学家，以研究整系数代数方程的（整数）解而闻名后世。我们对丢番图的了解主要来自5世纪的一本希腊文集，他的生卒年已不可知，我们只知道他在公元280年或298年去世。历代相传的丢番图墓志铭是一道趣味数学题，人们从中可以推算出他的寿数。这个墓志铭有多种语言、多种版本流传，我们的译本如下：

丢番图氏眠于斯，刻石立碑藏趣题。汝若能通代数学，一生梗概便可知：

其生之始六分一，细算起来是儿时。再经十二分之一，青春焕发起须髭。

七分之一看又过，终得伊人结连理。五番寒来又暑往，秋水望穿生贵子。

半生幸有儿陪侍，悲儿壮年先父死。排遣伤痛待如何？精研数论只为彼。

四载时光弹指飞，一朝限至魄西归。丢翁享寿共几许？推敲文句探幽微。

对现代人而言，丢番图以所谓“丢番图方程”而著名，作为现代数学术语的“丢番图方程”，所指的是含有多个未知量的整系数代数方程。特别的是：一个方程一旦被称为丢番图方程，就意味着人们在研究中只关心它的整数解。

根据定义，丢番图方程多得不可胜数，而其中最著名的首推大名鼎鼎的毕达哥拉斯方程：

x²+y²=z²。

这个方程的最小（正整数）解就是我们熟知的“勾三股四弦五”，即

3²+4²=5²。

现在我们来寻找毕达哥拉斯方程的所有解，也就是寻找所有满足x²+y²= z²的（正整数）三元组。由于这个方程对应着勾股定理，因此它的解对应的是三边边长都是正整数的直角三角形。换句话说，我们的问题是寻找所有“勾股数”的公式。

首先，我们注意到6²+8²= 10²本质上不是一组新的解，因为6，8，10可以方便地由3，4，5乘以2而得到。从一组解出发，我们可以用乘以某个整数倍的方法得到另外无穷多组解，但它们并非是我们的兴趣所在，因为它们相应的直角三角形都相似。为保证我们得到的是新的直角三角形，我们应该只考虑所谓的“本原解”，即x，y，z没有公因数的解。这事实上是说x，y，z中任何两个都没有公因数，因为如果某两个有公因数，则显然第三个数也将有相同的因数。

其次，我们需要一点同余理论的帮助。依定义，所有的奇数2k+1都有2k+1≡±1（mod 4），因此奇数的平方满足（2k+1）²≡1（mod 4）。据此，倘若x，y都是奇数，则其平方和是偶数，这使得z必然是偶数。但该平方和对模4与2同余，而偶数的平方却是4的倍数，也就是对模4与0同余。这个矛盾说明，x和y不能同时为奇数。

另一方面，x与y也不能同时为偶数，否则z也是偶数，所得的解也就不是我们所要求的本原解。

因此，我们不妨假设是x是奇数而y是偶数，这样一来，z也必须是奇数。我们记y=2u，则方程可以写成

x²+4u²=z²。这时x，u，z中的任何两个都没有公因数，但是

因为x和z都是奇数，所以（z+x）与（z-x）都是偶数，我们记

则我们马上得到：

u²=sr。

由s和r的定义可得：z=s+r，x=s-r。如果s和r有公因数，则z和x也有。但z与x是互素的，因而s与r也互素。根据这个结果，s和r没有可以相匹配的素因数，所以方程u²=sr使得s和r都必须是完全平方数。记r=n²，s=m²，则有u=mn，并且

这样，我们就证明了：如果x，y，z是一组本原解，则它们必然具有上述形式。而由于x，y，z是互素的自然数，我们容易推得这样三条对m和n取值的限制：（一） m必须大于n，这样x才会是正数。（二） m和n必须没有公因数，否则x，y，z都会有相同公因数的平方。（三） m和n不能同为奇数，否则x，y，z将全部为偶数。因此，如果我们让m和n遍取所有满足这三条限制的自然数，那么我们将得到所有的本原解。

很明显，如果去掉第二及第三条限制，那么我们得到的也是勾股数。只不过它们未必是本原的。最后，我们下面举几个具体的例子。细心的读者也许会注意到：勾股数的乘积总是60的倍数。从上述勾股数表达式出发可以证明这个性质，有兴趣的读者不妨自己尝试。

我们用以上这些结果来证明一个几何定理：以勾股数为边长的三角形之内切圆半径长度恒为整数。

这个定理所说的事实并不是很显然的。内切圆半径与三角形边长看起来似乎并没有充分的关联，使得当边长为整数时内切圆半径也是整数。然而，这个定理的证明却是容易的。假如x，y，z是x²+y²=z²的整数解，则上图中的C是直角，且三角形的面积为xy/2。但三角形的面积同时也等于BOC，COA，和AOB这三个三角形的面积和，这就是说

据此可以解得：

我们知道x，y，z满足上节中我们发现的公式，把这些公式代入r的解，然后化简，则有

这样，我们不仅证明了内切圆半径是一个整数，并且得到一个额外的结果——发现它究竟等于哪个整数。我们前文给出了三个例子，其内切圆半径依次是2，4，6。由于第二例是勾股数（3，4，5）的4倍，因而其内切圆半径也放大了4倍。这告诉我们，（3，4，5）为边长的三角形之内切圆半径等于1。这，说不定您以前不知道？

勾股数古老的公式

德国修士迈克尔·施蒂费尔（1487—1567）发现了一种构造勾股数的方法。首先，他创建了如下的带分数序列：

只要将序列中的每个带分数都改写成假分数，则分数的分子和分母就是一组勾股数中的前两个。例如，我们取序列中的第4项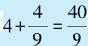，，那么就存在一组形如（9，40，c）的勾股数。据勾股定理，c²=9²+40²=81+1600= 1681，而1681的平方根等于41。因此，这组勾股数就是（9，40，41）。

勾股定理的证明

勾股定理有多达数百种的证明方法，通常认为最早的证明是由毕达哥拉斯给出的。有意思的是，在19世纪，美国第20任总统加菲尔德发表了一种新的证明方法，他考虑如上直角梯形：

很显然，这个梯形的面积等于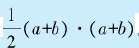。同时，它也等于图中三个三角形的面积和，即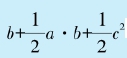。化简上述等式，即得到勾股定理。

拿破仑定理

有意思的是，美国有加菲尔德总统给出勾股定理的证明，法国则有拿破仑发现数学定理。通常版本的“拿破仑定理”是这样的：

“以任意三角形ABC的三条边为边，向三角形ABC外构造三个等边三角形，则这三个等边三角形的中心恰为另一个等边三角形的顶点。”

如右图所示，ABX，BCY，CAZ都是等边三角形，O，P，Q分别是它们的中心，则三角形OPQ是一个等边三角形。

在一个平面上，会有多少不共线，但两两之间的距离为整数的点？显然，共线的情形会有无穷多个点，因为直线上到某给定点距离为整数的点相互间的距离也是整数。但当我们要求所有的点并不完全在同一条直线上的时候，问题就变得有趣了。

我们考虑除了一个点之外，其他点都在同一条直线时的情形。这种思路非常实惠，它排除了解决问题时不必有的困难——我们的问题并不要求所有的点必须分散到平面的各个角落，只是要求它们不全部共线。

在仅有一点位于直线之外的情形下，我们可以构造出任意大的点集，使其中任意点到其他点的距离都等于整数。构造的方法并不复杂，就是利用勾股数。具体地说，对给定的自然数k，我们找出一个整数，使得它可以与k个不同的整数配合起来构造勾股数。这样一来，相应的k个直角三角形共用同一条直角边，则另一直角边的顶点位于同一条直线上，而所有这些三角形的顶点间的距离都是整数。

先举一个最简单的例子，我们知道（3，4，5）和（5，12，13）是两组勾股数，它们对应两个直角三角形。把第一个三角形放大4倍，则我们得到边长为（9，12，15）的直角三角形，它与三边为（5，12，13）的直角三角形共用一条边长为12的直角边。以这条边为共同边，我们得到右边的图形。图中两个三角形总共有四个顶点，它们两两之间的距离都是整数！

现在，假设我们要求7个满足问题条件的点。我们已经知道毕达哥拉斯方程存在无穷多组本原解，而且知道只要逐一代入m-n数对就可以据公式写出任意多组解。为解决这个问题，我们只需要找出五组勾股数，为了更详细地解说具体做法，我们先找出五组本原勾股数：

我们把第三组的直角边换个次序，写成（8，15，17），则这五组勾股数就是：（3，4，5）、（5，12，13）、（8，15，17）、（7，24， 25）和（9，40，41）。求五个组的第一个数之最小公倍数，我们得到2520。以这个数为短直角边放大相应的直角三角形，得到（2520，3360，4200）、（2520，6048，6052）、（2520，4 725，5355）、（2520，8640，9000）和（2520，11200，11480）。因此，我们可以按以下方法在（x，y） -平面上选点：以原点O为第一个点，选择Y轴上距离原点为2520的点为第二点，其他五个点则放在X轴的正方向上，与原点的距离依次为3 360，6048，4725，8640和11200。这样，我们就得到7个点，它们两两之间的距离都是整数。

在确定5个直角三角形公共直角边边长的时候，我们使用的是3，5，8，7，9的最小公倍数。事实上我们可以直接把这五个数相乘作为边长，只是直接相乘得到的边长要大一些。很显然，以上这种构造方式可以推广到任意多个直角三角形，因此我们可以构造出任意大的满足问题条件的点集。

我们很轻易地就解决了一个丢番图方程，即毕达哥拉斯方程：

x²+y²=z²。

因此我们接下来考虑一般情形：对n>2，方程

xⁿ+yⁿ=zⁿ

的正整数解是什么？如果您觉得毕达哥拉斯方程真是太容易了，那么这个则相当相当困难。这个问题是费马提出来的，他断言这个问题没有正整数解，并宣称自己作出了证明。为区别于我们介绍过的费马小定理，费马的这个断言被称为“费马大定理”。这个问题曾经难倒了三百年来最优秀的数学家，直到1995年才被英国数学家安德鲁·怀尔斯所证明。

在20世纪以前的200多年时间里，数学家们在这个问题上考虑得最多的是对特定的n值，费马大定理能否被证明的问题。其中，n=4情形的证明是最简单的，这个证明虽然有点儿长，但解决方法完全是初等的。我们特意在这里介绍这个证明，因为它很好地阐释了著名的“无穷下推法”。

如果这个方程不存在本原解，那么它自然也就没有解。因此，就像讨论毕达哥拉斯方程时一样，我们只关注方程的本原解。现在，我们作反证假设，假设某一组互素的x，y，z满足方程x⁴+y⁴=Z⁴。取z=Z²，则x，y，z是方程

（1） x⁴+y⁴=z²

的解。也就是说我们得到

（x²）²+（y²）²=z²，

其中x²，y²，z是一组本原勾股数，因此x²与y²必然是一奇一偶。我们不妨说y²是偶数，因此，根据勾股数的构成公式，我们有

这里，m>n，m与n互素且不都为奇数。实际上这里的n必须是偶数，不然的话，m为偶数而n为奇数，则x²是4的倍数减1，即

x²≡0-1 （mod 4）≡3（mod 4），

这是不可能的，因为奇数的平方是四的倍数加1。所以说，我们可以设n=2k，其中k与m互素，且

y²=2m·2k。

根据我们此前的讨论，没有公因数的k与m都必须是完全平方数，即

m=r²，k=s²，y=2rs。

不仅如此，我们还可以得到如下三个结论：（1） r与s互素，因为k与m互素；（2） r>s，因为x²是正数；（3） r也是奇数，因为m是奇数。这就是说，

x²=r⁴-4s⁴，

或

x²+4s⁴=r⁴。

这样，我们得到一组新的勾股数（x，2s²，r²），因此又有：

其中的p，q的角色正像是此前的m，n。经由我们已经熟悉的讨论过程，可以由pq=s²推出p=a²及q=b²。于是，我们最终得到

（2） r²=a⁴+b⁴。

然而，这个方程与

（1） z²=x⁴+y⁴

的形式完全相同。我们因此证明：如果（1）有解，则（2）也必须有解！

这一连串推导所得的结果乍一看好像没有什么意义，然而，由z的表达式

z=m²+n²=r⁴+4s⁴，

我们发现z>r。也就是说，（2）的解是与（1）不同的一组新解，而且这组解（a，b，r）所含的自然数比原来的解（x，y，z）更小。不仅如此，由于a，b来自本原勾股数的构成公式，它们都必然是正整数。这就是说，（a，b，r）是一组正整数，这组新解不是“退化”的。

从（a，b，r）出发再重复上述步骤，我们又会得到一组更小的、新的、非退化的解。如此继续重复，将各组解依次记为r_i，a_i，b_i，则我们得到一个严格下降的序列：

r>r₁>r₂>…>0。

由于r是有限的，r_i均为正整数，所以这个序列不可能无限地继续下去。然而上述论证过程表明，原假设之下序列是可以无限继续的——这就是确然无疑的矛盾了！这一矛盾证明原假设是错误的，所以结论即为：不存在满足方程

x⁴+y⁴=z⁴

的正整数组x，y，z。

安德鲁·怀尔斯

安德鲁·怀尔斯出生于1953年4月11日，是一位任职于普林斯顿大学的英国数学家。

因为少年时读到一本介绍费马大定理的、名为《最后问题》的科普书，怀尔斯从此对费马大定理的证明产生持久而浓厚的兴趣。在1980年代，数学家们发现，日本数学家提出的谷山—志村猜想的某个特例可以推导出费马大定理。受此启发，怀尔斯连续七年秘密进行关于这个特例的研究。他以发表不相关的小论文来掩盖自己真正的工作，只有妻子知道他真实的研究方向。

经过七年不懈努力，怀尔斯发明许多新的数学概念和证明技巧，终于证明出谷山-志村猜想的这个特例，从此解决了费马最后猜想。

1993年6月，怀尔斯在牛顿研究所安排了三场演讲，在最后一场演讲中，他向听众公开了演讲的最终目标是费马大定理的证明，当场引起巨大的轰动。

不久之后，有人发现怀尔斯的证明存在一处不易修补的错误，这让数学界很多人对费马大定理的解决又产生了怀疑。但有惊无险，怀尔斯和他的学生在一年多后填补了这个漏洞，最终完成了费马大定理的证明。(www.chuimin.cn)

考虑我们熟悉的数轴。数轴上与原点距离等于有理数的点称为“有理点”。由于任何两个不同有理数的平均数是介于它们之间的另一个有理数，因此，任何两个有理点之间总可以找到另外的有理点。事实上，稍加思考就知道，任何两个有理点之间存在无穷多个有理点。由于这样一种现象，我们说有理点在数轴上是“稠密的”，有理点的集合是一个“处处稠密集”。

相似地，在具有平面直角坐标系的平面上，我们将两个坐标的数值都是有理数的点称为“有理点”，不是有理点的其他所有点则称为“无理点”。不难证明，有理点在平面上也是处处稠密的。然而，平面上的无理点也同样处处稠密，而且实际上它们比有理点要多得多。事实上，有理点集可以和自然数集合一一对应起来。也就是说，我们可以把所有的有理点用1，2，3，…编号排列，因此我们说有理点集是一个“可数集”。然而，无理点集是不可数的，所以它们事实上比有理点多得多。关于这一点，有兴趣的读者可以自己查找相关的资料。

我们刚刚介绍了费马大定理在n = 4时的证明。它告诉我们，方程x⁴+y⁴=z⁴没有正整数解。而这等于说，方程

x⁴+y⁴=1

除了（0，1）和（1，0）之外没有其他非负有理数解，否则n= 4时的费马方程将有正整数解。

一个方程的图形指的是所有满足该方程的点构成的曲线。方程x⁴+y⁴= 1的曲线如右图所示，它通过（0，1）、（1，0）、（- 1， 0）和（0，- 1）四个有理点。但除此之外，没有其他有理点可以满足方程。因此，这条曲线穿行于处处稠密的有理点集之中，却没有再碰触这四个点以外的任何有理点。

我们这本小书所讨论的对象主要是数字，但是上面这张图实在太有意思了，所以我们暂时离开主题，来讲一点相关曲线的图形。如上所示，x⁴+y⁴= 1的图形是一条封闭曲线，它关于两条坐标轴都对称，形状介于圆和正方形之间，而看起来更接近正方形。

对所有自然数k，我们来系统地考察方程|x|^k+|y|^k=1的图形。我们很容易知道，所有这些图形都是关于两条坐标轴对称的封闭曲线，而且都经过（0，1）、（1，0）、（- 1，0）和（0，- 1）四个有理点。我们还知道，当k = 1时的图形是一个斜置45度的正方形，k = 2则是大家熟知的圆。而且，这两种曲线都经过无穷多个有理点。对k>2，由费马大定理我们知道，曲线上除了上述四个有理点之外不再有任何有理点。

我们考虑第一象限里的图形。此时，曲线|x|^k+|y|^k=1在横坐标为x时的纵坐标是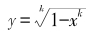。在0<x<1时，x^k显然随着k的增大而减小，因此对相同的x值，曲线在第一象限里的纵坐标y随着k的增大而增大。换句话说，k越大则曲线越“胖”！这不仅解释了x⁴+y⁴=1的形状比圆“胖”很多的原因，而且也指出了这样一个事实：随着k的不断增加，|x|^k+|y|^k=1的形状越来越接近正方形！

那么，对小于1的正分数次幂α=p/ q，方程|x|^α+|y|^α=1的图形又是怎么样呢？与上述相似的分析表明，它的图形将是

在|x| +|y| = 1曲线之内的四角星形状，并且随着α的减小越来越“瘦”！我们这里给出|x|^1/2+|y|^1/2=1的图形，有兴趣的读者可以借助MatLab或其他数学软件来绘制这类曲线。

x⁴+y⁴=1上虽然有理点只有可怜的四个，但它毕竟还没有避开所有的有理点。而事实上，完全避开有理点的平面曲线是存在的。在本章的开头我们曾指出：方程x²-3y²=1有无穷多组正整数解，但方程x²-3y²= 2则连一个有理数解都没有。这就是说，前者的曲线经过无穷多个“格点”——即坐标为整数的点，而后者的曲线上则连一个有理点都没有！

可数与不可数

自然数集N={1，2，3，…}是一个无穷集合，但是，我们可以依照它们的顺序，即1，2，3，4这样的顺序数下去。这种可以按顺序（无休止地）数下去的无穷集合，就是“可数的”无穷集合。

不仅自然数集是可数的，所有整数的集合也是可数的。对所有整数的集合，我们可以按0，1，-1，2，-2，3，-3，…这样的顺序无休止地数下去。

总而言之，对一个集合A，如果存在一个从它到自然数集N上的一一映射f：A→N，那么它就是可数的。换句话说，对可数的无穷集合A，我们可以把它的元素都按顺序列出来，写成{a₁，a₂，a₃，…，a_n，…}的形式。

如果A和B都是可数无穷集合，那么A和B合在一起形成的也是可数的无穷集合。因为，我们可以把它们按a₁，b₁，a₂，b₂，a₃，b₃，…的顺序数下去。

有些无穷集合是不可能“按顺序数下去的”，这种集合就称为“不可数的”。

与费马方程不同的是，方程

x³+y³+z³=w³有无穷多组正整数解，最小的解是

3³+4³+5³=6³。

对有些w值，这个方程的解不止一个。对100以内的w，解最多的是w=87和w= 90。对这两个w值，方程x³+y³+z³= w³都有四组解。而在所有小于500的w中，w= 492时方程x³+y³+z³= w³的解数最多，它总共有13组解！也就是说， 492³可以写成13种不同的三自然数立方和的形式！我们将w=492时的（x，y，z）列表如下：

17、18世纪的加农炮的炮弹是球形的，当时的士兵喜欢把它们堆成有规则的堆垛，因为这样堆放不仅好看，而且还容易计数。有一种堆放方式是在最底下排列n×n个炮弹，然后逐层减少，堆放成一个金字塔的形状。一个著名的趣味数学问题是所谓的“加农炮炮弹问题”，它是19世纪法国数学家卢卡斯提出来的，这个问题要求底层正方形的边长，使得整个炮弹金字塔的炮弹总数恰好为完全平方数。也就是说，要求解如下的丢番图方程：

1²+2²+3²+…+k²=N²。

由于左边的和等于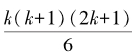，所以问题就转化为求自然数k使得等于完全平方数的问题。有意思的是，这个问题只有唯一的一个解，即k= 24，N= 70，炮弹总数为4900。

现在我们来攻克另一个有唯一正整数解的丢番图方程：

y²+2=x³，

其唯一正整数解为

y=5，x=3。

为了指出通向证明的道路，我们需要一起来回顾一些中学的代数知识。我们成长过程中经历过的大多数小学课本都包含有这样或那样的错误，其中之一是说，对任何x，a， b，都有

然而这个式子其实并不总是成立的，当x是负数时就未必正确，例如

而

如果我们声称

，因此上述等式可以成立，那么我们虽然找来了一个勉强能说得通的理由，却引入了另一个谬误：因为只要没有正负符号，则4^1/2与两个表达式都被认为等于2。如果我们想表达的是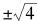，我们必须明确写出正负号。此外，这个谬误的另一种表现方式是说，而这个式子在a，b同为负数时同样是错误的：

您是不是觉得我们在说不相干的事情？不是的，我们指出的是中小学里经常忽视负数的开平方，或者说忽视虚数的存在。而虚数恰好是我们给出方程y²+2=x³解的唯一性证明的关键。

我们下面将对方程左侧作因式分解。有的读者可能会说，y²+2是不能分解的，但并非如此。y²+2虽然不能分解为实因式的乘积，在考虑复数的时候却可以分解：

现在，我们转而考虑另一种对象：形如

的数，其中a，b都是普通的整数。也就是说，如果我们用Z表示整数集，则我们现在考虑这样的数集：

对这个集合里的两个数做加、减、乘法，它们的结果也仍然在集合里。甚至，我们可以将这个数集里不能再分解的数定义为它的“素数”。简单地说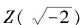，与整数集的性质非常相像，它也有“唯一分解定理”。

总之，我们的这个因式分解把y²+ 2分解成了在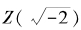范围内的“素因式”。根据唯一分解定理，由于与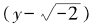的乘积等于x³，它们也都必须是Z里的立方数。这就是说，

无论是轻信或者拥有足够的知识，总之我们承认：如果两个复数相等，那么它们的实数部分必须相等，虚数部分也必须相等。据此，考察上式中的系数，我们就得到

1=3u²v-2v³=v（3u²-2v²）。

由于上式中的v是普通整数，所以v只能取1，而u则只能是±1。计算上式中的实部，立刻得到：y=±5。

以上只是证明的一个梗概，因为论证过程中还有两个环节没有证明。第一个是假定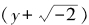与在Z范围内是素因式。这确实没有问题，我们可以证明这两个都不能分解为其他同类型因式的乘积。然而，我们的证明还是不够完备，第二个缺环更为重要——我们如何证明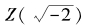里的素因式分解是“唯一”的？这一点也可以用初等的方法来证明，但证明细节相对复杂，我们这里不作介绍。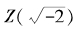里的素因式分解是“唯一”的，但对其他根式而言，相应的未必有“唯一分解定理”。例如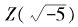就没有。事实上，对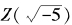我们很容易找到例子：

6=2×3，

且

不难证明，2，3，，在范围内是不能再分解的素因数。因此，整数6在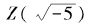中存在两种不同的素因式分解！

虚数与复数

我们知道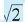，不是有理数，但是它等于1. 4142…，确实对应着数轴上的一个点，所以它是一个实数。相应地，任何实数的平方都是正数或零。因此，如果我们考虑对一个负数开平方，那么它就不可能是实数。由于数学研究及应用的需要，人们把也负数的开平方也看作数，由于它们不是实数，人们将它们称为“虚数”。所有虚数中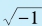，拥有特别的地位，它和1相似，是“虚单位”，通常记成i。

所谓“复数”，就是实数与虚数的“复合形式”。换句话说，如果a和b都是实数，那么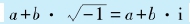就是一个复数。加号两边分别称为这个复数的“实部”和“虚部”。

复数的运算法则与普通的数没有区别，只要在遇到i·i时，将它用-1代替就可以了。例如，（1+2i）·（2-i）= 1·2-1·i+2i·2-2i·i=2-i+4i-2·（-1）= 4+3i。

复数在高等数学与物理中都非常重要。有趣的是，关于复数有一个很漂亮的公式：

e^iπ+1=0，

它被称为“最美数学公式”。

在上一小节所讨论的丢番图方程中，如果把2换成另外的常数，我们都将得到一个新的问题。每一个这样的问题都需要自己的解决方式，而且它们的答案之间几乎都毫无干系。已经被解决的这类方程为数不多，其中，方程

y²-7=x³

没有（整数）解。而方程

y²-17=x³

则有八组解。对这个方程尝试小的x值时，它的解似乎到处都是，因为x= -2，-1，2，4，8时，我们都能够得到相应的y。然而，在这五个解之后这个方程只有另外三个解，它们是x=43，x=52和x= 5234。对我们而言，得到最后一个解相当不容易，这时的x³=143384152904，已经是一个天文数字了。

如果我们突发奇想，提出这样一个问题：连续三个自然数的乘积有没有可能是一个完全平方数？将三个自然数中间的那个记为n，则这个问题就等于是求丢番图方程

n³-n=m²

的解，这看起来和上面讨论的那组丢番图方程有些相像。那么，问题的答案会是什么呢？我们来考察一下。

我们首先把方程左边改写成n（n²-1）。稍加思索，我们立刻发现n和（n²-1）是互素的。因此，如果n（n²-1）是完全平方，那么n和（ n²- 1）都必须是完全平方。然而，如果（n²-1）= k²，则（1，k，n）是一组勾股数，而这是不可能的，根据勾股数的构成公式，“勾”最小数值是3！因此，我们得到结论：连续三个自然数的乘积不可能是一个完全平方数。

上面的问题没有解，如果我们放宽些条件，考虑“等差自然数列连续三项的乘积”，它有没有可能是完全平方数？同样假设中间项是自然数n，而将公差记为k，则我们所考虑的乘积为n（n²-k²）。为简化问题，我们不管n和（n²-k²）是否互素，先考虑n是完全平方的情形。此时，（n²-k²）也必须是完全平方，即n²-k²= m²。也就是说，我们要求n等于一个完全平方数，而且（k，m，n）是一组勾股数。这是不难做到的，对任何一组勾股数（a，b，c），将它放大c倍就可以了。例如，取n= 25，则公差取k= 15或k= 20都可以，得到的三个数项分别是{10，25，40}和{5，25，45}，它们的乘积分别是100的平方和75的平方。

我们从小时候就知道完全平方公式：

（a+b）²=a²+2ab+b²。

因此，对任何两个自然数a和b，a²+2ab+b²的值都是一个完全平方数。这个重要的基本知识有时候会带来错觉——我们有可能一不小心就认为a²+ab+b²肯定不会是完全平方数。然而，这种认识是不正确的，一个不是完全平方形式的代数式可以是完全平方数，只要我们代入恰当的数字。那么，a²+ab+b²在什么情况下会是完全平方数呢？这个问题又导致一个丢番图方程：

a²+ab+b²=c²。

显然，如果一组解（a，b，c）中的a和b有公因数p，则p也是 c的因素。将a，b，c都除以p，我们将得到方程的另一组解。和以前一样，我们说这种解不是“本原”解。由于我们关心的依然是本原解，因此，我们假设a和b互素。现在，我们把原方程改写成：

（a+b）²-ab=c²，

移项作因式分解，我们得到

（a+b+c）（a+b-c）= ab。

由于等式的左边和右边都是整数的乘积，因此我们可以假设m，n，r，s都是自然数，并且：

a=mn，

b=rs，

a+b+c=mr，

a+b-c=ns。

将后两个等式相加，并将a和b的表达式代入，则我们得到

2（mn+rs）= mr+ns。

移项整理，得

m（2n-r）= s（n-2r）。由于a和b互素，因此它们相应的因数m和s也互素。这样，我们就推出：2n-r是s的整数倍，n-2r是m的整数倍。因此，

2n-r=ks，

n-2r=km。

从这两个式子很容易推出：

3r=k（s-2m），

3n=k（2s-m）。

由于a和b互素，因此n与r也互素。这样，k只能取±1或者±3。考虑k=-1的情形，则

r-2n=s，

2r-n=m。

把这两个式子代入a和b的表达式，我们得到：

a=mn=（2r-n）n=2nr-n²，

b=rs=r（r-2n）= r²-2nr。

再将上述两个式子代入原方程，即有：

c=n²-nr+r²，

也就是说，

是原问题的整数解。相似的推导不难发现，k的其他情形并没有给出本质上不同的解。总之，从以上公式可以求得问题的所有本原解。当然，对r和n有两个限制条件：一是要求r大于n的两倍，因为这样得到的a和b才都是自然数；二是要求n与r互素，因为这样的话a和b才会互素。

有理数集是可数的

为简单计，我们只考虑正有理数的集合。我们知道，每个正的有理数都可以写成既约分数q/ p。我们把这些有理数按这样的原则来排序：（1） p+q小的排在前面，（2）对p+q相等的分数，p较小的排在前面。这样，我们就得到：1/1， 2/1， 1/2， 3/1， 1/3， 4/1， 3/2， 2/3， 1/4，…。换句话说，我们可以把正有理数按这样的顺序无休止地数下去！所以说，正有理数集是可数的。

当然，我们可以给正有理数集安排不同顺序，右图就是另一种排序：

实数集是不可数的

我们来证明[0，1]区间上所有实数的集合是不可数的。我们采用反证法：假设[0，1]区间上所有数的集合是可数的，那么这个数集就可以写成{a₁，a₂，a₃，…，a_n，…}。当然，其中每一个数都是小数，因此我们可以把a_n写成十进制小数，即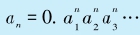。现在，我们构造一个十进制小数x=0. x₁x₂x₃…x_n…，使得：（1） x_n≠0，且x_n≠9，（2） x_n与a_n小数点之后的第n位不相等，即x_n≠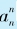。这样一来，x是[0，1]区间中的数，却不与集合{a₁，a₂，a₃，…，a_n，…}中的任何一个元素相等。这证明，{a₁，a₂，a₃，…，a_n，…}并没有能够把[0，1]区间中所有的数都列入！这一矛盾证明，[0，1]区间中的数是不可数的。