无理数及超越数：数字丛林的冒险之旅

所有的完全平方数构成一个无穷数列，我们按顺序写出前几项：

1，4，9，16，25，36，49，64，…

在这个数列的前四项里，我们发现第4项是第2项的四倍。好联想的读者可能会闪过一个念头：数列中有没有哪一项会是另一项的两倍或者三倍呢？这个问题的答案，对一些人而言并不是很显然的。然而，无论检查多少项，我们都绝不可能找到一个两倍或三倍于另一个完全平方数的完全平方数。

以三倍为例，我们可以肯定，没有完全平方数是另一个完全平方数的三倍。为什么呢？我们可以用反证法来证明——

假设方程x²= 3y²至少存在一组正整数解。我们在方程的所有正整数解组（x，y）中，考虑它的“最小解组”，即x值最小的解组，把它们记为（a，b）。

由于a²=3b²，即a²可以被3整除，而3是一个素数，所以a必然是3的整数倍。因此，存在自然数a′，使得

a=3a′。

将这个式子代入等式a²=3b²，我们得到

3a′²=b²。

这样一来，我们发现（b，a′）也是方程x²= 3y²的一组正整数解。因为b显然小于a，所以这组解的出现与（a，b）是“最小解组”的选择相矛盾。这就证明，方程x²= 3y²不可能有“最小解组”，因而根本不可能有正整数解组。

完全平方数的商a²/ b²绝对不可能等于3，这等于说不可能找到整数a和b，使得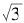=a/ b。众所周知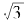，这个记号表示的是“3的平方根”。从几何的观点看，它是面积等于3的正方形的边长。我们这里的结果是说：面积等于3的正方形之边长不可能写成两个整数的比例。从古希腊开始，数学家就称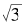是“无理的”，意思是“不能写成（整数之）比例的”。

这里，我们有必要暂时岔开话题，谈一谈“无理数”这个术语。在英语中，“有理数”是rational number，而“无理数”则是irrational number。它们命名的源头在英语中是ratio这个词，意思是“比例”。虽然历经从古希腊语、拉丁语到英语的演变过程，古希腊发现无理数的毕达哥拉斯学派的意思一直传承着，并没有改变，也就是说，“有理数”就是可以写成整数之比例的数（或者说是分数），而“无理数”则是不可以写成比例的数。

那么，中文为什么要将这两个术语翻译成“有理数”和“无理数”呢？翻译者的真正想法我们不能确切地知道，但是我们可以从毕达哥拉斯学派的一则故事来理解这种译法：据传，毕达哥拉斯学派有一个成员用与上述相似的推理方式，证明两直角边长度均为1的直角三角形的斜边长度2无法写成两个整数的比例，这在学派内引起轩然大波！毕达哥拉斯学派信奉“万物皆数”——整个宇宙因此和谐而优美，而他们心目中的“数”来自自然数的四则运算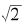，不能写成整数比例的事实，破坏了学派的基础信条，因此，换作英语来说， irrational在他们的心目中简直就是unreasonable！

好了，我们现在把话题拉回来。前文的分析同时告诉我们，完全平方数的数列中也没有两个项的比例等于2与3之外的任何其他素数，因此素数的平方根都是无理数。此外，虽然6不是素数，一个完全平方数也不会是另一个完全平方数的6倍，因此也是无理数。我们不难证明，完全平方数的平方根是整数，而除了完全平方数之外，其他的自然数的平方根都是无理数。

相似地，没有立方数会是另一个立方数的素数倍，其他情形亦与上述类似。总之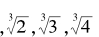等等都是无理数。与无理数对应地，“有理数”是可以写成分数形式的数，它们可以写成两个整数的商。

我们注意到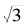，是方程x²-3= 0的解是x³-3= 0的解。因此，这里出现的无理数有一个共同点：它们都是整系数多项式方程的解。由于整系数多项式方程也称为“代数方程”，因此它们的解就被称为“代数数”。显然，平方根和立方根都是代数数，也是代数数。需要注意的是，有理数显然也是代数数的一部分，它们是一次整系数方程的解。

数学中有“实数”的概念，粗略地说它对应着数轴上的点。实数中除了代数数还有别的数存在，这些并非代数数的实数称为“超越数”。我们用一个图来表示这些概念的关系：

无理数的悲剧

毕达哥拉斯学派相信世界是和谐的，和谐表现为（简单的）自然数的比例，五度相生律就是这种哲学一次极为成功的体现。然而，在研究单位正方形（边长等于1）对角线长度时，毕达哥拉斯的得意门徒希帕索斯却证明：这个我们现在称为根号2的数，绝对不可能表示成一个比例。换句话说，这条对角线的长度不是有理数！这个发现动摇了整个毕达哥拉斯学派的哲学根基，为保全门派，毕达哥拉斯学派的学者们全体发誓保守这个秘密，并为灭口而秘密杀害希帕索斯。

超越数

因为对具体的物体计数，人类首先产生自然数的概念。通过自然数的加、减及乘法运算，我们得到包括正整数、零以及负整数的所有整数。整数间的除法运算，让我们得到分数。所有分数都是比例，它们构成“有理数”的集合。

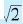是无理数，但它是方程x²-2=0的根。因此，人们考虑以整数为系数的多项式方程a₀xⁿ+a₁x^n-1+…+a_n-1x¹+a_n=0。当一个数是某个整系数代数方程的根时，它就被称为一个“代数数”。这样一来，凡是可以用整数的有限次加、减、乘、除，以及开方运算得到的数，都是代数数。

很显然，自然数集是整数集的子集，整数集是有理数集的子集，有理数集是代数数集的子集。

我们很熟悉“数轴”，它上面的每一个点都表示一个数，这些数通称为“实数”。实数中有很多很多的无理数，这些无理数中“绝大部分”不是代数数，它们不能表示成任何代数方程的根，我们将这类数称为“超越数”。超越数虽然很多很多，但人们直到19世纪才证明超越数的存在，而π和e，则是两个最著名的超越数。

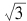不能写成分数，那么它写成十进制小数是多少？怎么计算？这是自古以来人们就很关心的问题。古人没有计算机，但他们发明了一位一位逐步计算平方根的方法。刘徽在《九章算术》的注解里给出的方法很有趣，值得我们做个介绍。

考虑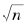的计算。我们将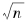的整数部分记为a₀，小数点后第k位记为a_k。在计算出第k位开平方的结果后，我们将已经得到的结果记为x_k，即x_k=a₀. a₁…a_k。首先，我们寻找自然数a₀，使得它满足不等式：

也就是说，计算方法的第0步是估算出a₀，这当然不是困难的事。按照我们的约定，此时有x₀=a₀

很明显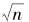，小数点后的第一位为a₁的充分必要条件是：

（x₀+10^-1·a₁）²<n<[x₀+10^-1·（a₁+1）]²。

展开不等式并整理出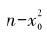的前半部分，则我们得到：

因此，计算a₁的具体办法分两个步骤：先从n中减去，然后对剩下的数值估算a₁，而估算的方法是对不同的a₁试算10^-1a₁·（2x₀+10^-1a₁），比较它与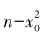的大小。如果化成整数的除法运算，这等于是在这一步里将两个数都乘以10²——就是说，在除法算式里给被除数添加两个0，而试算的除数和商则分别成为（20x₀+a₁）和a₁。

计算出a₁之后我们得到x₁=a₀. a₁。现在，我们要求a₂满足：

因此

这就是说，a₂的计算同样是两个步骤：先计算从n中减去已经得到的开平方数x₁的平方，即计算n-（a₀+10^-1·a₁）²的结果，然后再用估算a₂，即对不同的a₂试算10^-2a₂·（2x₁+10^-2a₂），比较它与n-x²₁的大小。如果我们继承上一步的除法算式，那么，我们现在需要的是在原有的除法算式里在余数后面继续添加两个0，从而化成整数间的除法运算。此时，试算的除数和商分别是（200x₁+a₂）和a₂。

从以上两个步骤，我们已经发现了计算a_k步骤的规律性，即：作除法，在余数后面继续添两个0，然后，以除数（2×10^kx_k-1+a_k）和商a_k来试算a_k。为了更加形象，我们来看看计算3的前几步，注意每一步的被除数、除数和商数的算法：

根号3的近似估计

阿基米德在其著作《圆的测量》中，给出了3的平方根的近似值：

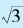这就是说，的值大约介于1. 7320261与1. 7320513之间。计算可知：≈1. 7320508，可见阿基米德给出了非常好的近似分数。

有意思的是，我们在第9章给出了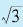的连分数，它的渐进数列的前十二项为

阿基米德给出的恰好是它的第九项和第十二项。事实上，如果根据这个渐进数列来给出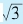的近似估计，我们通常应该给出

或

这说明，阿基米德不是用连分数的方法得到3的近似分数，但他究竟用的是什么方法，已经成为不解之谜。

通过上面的计算，我们可以算得≈1.732050807…。它的小数部分显然是无穷无尽的，因为有限小数可以立刻写成以10的某次方为分母的分数，而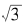却不能写成分数形式。那么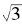，的无穷的小数部分会不会是循环的？这也不可能。如果您疑窦顿生，却拽了句文言来发问说：“何以知之？”那我们会回答说：“此易事也，君未细思耳。”确实，这个问题稍加思索就可以明了——

如果某数是一个无限循环的小数，比方说x是一个如下形式的无限循环小数：

x=0. a₁a₂…a_na₁a₂…a_n…

那么，它的循环节为a₁a₂…a_n，其长度为n，因此，

据等比数列的求和公式，我们得到：

这证明：无限循环小数可以表示成分数，因而是一个有理数。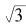既然不能表示成分数，它的小数部分当然也就不会是循环的。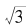不能写成分数，那么，我们能不能找到一个分数数列，使得这个数列以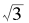为极限呢？答案是当然能，例如： 1. 7，1. 73，1. 732，1. 7320，1. 73205…就是。然而，这样逐步截取的前n位的数列并不能方便地用来作它的近似分数，因为它没有简单的通项公式。

逐步逼近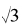而又有简单通项公式的数列是有的，中世纪的西方就已经做出了很高明而有趣的研究。事实上，这类分数数列有好多种，我们介绍其中最著名的两种。我们先用递推公式定义两个数列{a_n}，{b_n}：

然后，我们用以上两个数列定义一个新数列{x_n}：

根据数列{x_n}的定义，我们有

因此，

用数学归纳法不难证明：数列通项x_n的值总是正数，并且随着n的增加而下降。因此，根据“单调有界原理”，它必然趋于一个确定的极限——“单调有界原理”是一个高等数学中的定理，它的证明大大超出本书的范围，我们只能略而不论。假设{x_n}的极限为A，则根据通项公式，我们得到：

从上式我们容易得到A²= 3，这说明数列{x_n}的极限确实是。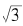

a_n/ b_n越来越接近，因此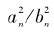越来越接近3，但是我们知道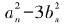永远不可能恰好等于3。那么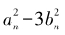，会是什么呢？答案非常出人意料！

回顾定义a_n和b_n的递推公式，我们立刻得到：

将右式展开，合并同类项：

这就是说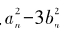，的值是恒定的，它并不随着n的变化而改变。而由于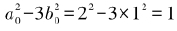，我们发现：的值永远等于1！

事实上，由a_n和b_n定义的数对（a_n，b_n），恰好是方程x²-3y²=1的所有解。而这个方程，则是著名的丢番图方程的一种。

最后，我们来考虑另一种逼近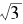的数列，我们用如下递推公式定义数列{y_n}：

如果我们以如下方式定义c_n和d_n：

则很容易证明：

有趣的是，数列{y_n}不仅以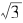为极限，而且它逼近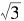的速度比上面介绍的{x_n}要快得多得多！此外，数对（c_n，d_n）同样满足丢番图方程x²-3y²=1，集合{（c_n，d_n） |n=0，1，2，…}事实上是{（a_n，b_n） |n=0，1，2，…}的一个真子集。

现在，我们把目光从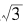这个无理数转向有理数。先来看看下面一组关于142857这个数的等式：

1×142857=142857，

2×142857=285714，

3×142857=428571，

4×142857=571428，

5×142857=714285，

6×142857=857142，

7×142857=999999。

为什么同样的六个数字的循环排列都是142857的整数倍？并非所有的数都出现如此有趣的现象。还有，为什么最后一个式子右边突然出现999999？

答案离我们并不很遥远——我们用除法将1/7写成十进制小数：

以上“答数”中紧接在小数点后的1说明10包含一个7。而余数是那个带圈的3，因此接下来是以7除30。这时，商是4而余数是那带圈的2，如此等等。这里，余数是问题的关键：在除以7的运算中，不是零的余数只能有6种。因此，在最多做六次除以7之后，就不可能再有新的余数出现，因而此前出现过的余数必然重复出现。在1再一次成为余数时，上述除法过程就会开始重复。所以，1/7的小数表示出现6位数字的循环的形式。

如果我们把2/7写成小数，我们得到相同的循环数字，只是循环开始的位置不同。这对3/7，…，6/7也都一样。但是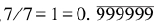，（用上划线表示循环节）。

七是一个素数，而它的倒数1 /7的循环周期等于7-1，即6。因为正如我们刚刚分析过的，这是它的循环周期最大可能的长度。具有这种性质的素数称为“全循环”素数。(www.chuimin.cn)

3是一个素数，它的循环周期最长可以为2，但1/3 = 0. 33333…，其循环周期长度只是1。13也是素数，因此1/13的循环周期最长可以达到12位数字，但1/13的除法做到6步时同样的余数就已经“绕”回来了，因而它的循环节也就开始了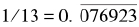：。那么，7是不是其倒数的循环周期达到最大长度的唯一整数？答案是否定的，下一个“全循环”素数是17：

在100以内的“全循环”素数总共有9个，可见“全循环”素数并不是很罕见。但准确判断哪一个素数是全循环素数的问题却长期困扰着数学界，至今没有人能给出答案。伟大的德国数学家高斯曾经苦思冥想，甚至得到重要而且深刻得多的结果，却也没能解决这个问题。

上一章所介绍的费马小定理告诉我们，由于7不能整除10，因此有

10⁶≡1（mod 7）。

忽略我们关于1/7的除法算式中的小数点，则它等于是10⁶除以7的除式。因此费马小定理已经告诉我们，那个最为关键的1，那个让小数开始循环的数，会恰好在什么时候出现。10⁶-1=999999恰好可以被7整除，因此，我们可以不作以7除1的运算，而是以7来除一串9构成的自然数，当我们除到余数等于零时的时候，我们就得到了1/7的循环节。这个办法实际上是寻求素数循环周期的另一个办法——为求表达简洁，我们以素数的“循环周期”来指它的倒数写成十进制循环小数时的循环节长度。

问题的困难之处在于，费马小定理并不保证6是使得同余式

10^e≡1（mod 7）

成立的最小指数e。对p= 7而言，e = p-1碰巧成立。但若考虑p=11，则尽管

10¹⁰≡1（mod 11），

但我们发现

1/11=0. 090909…，

循环周期仅仅等于2。定理说11必然整除9999999999，但对p=11这个例子，它凑巧可以整除99这个短小得多的数。

如果n是素数，而其循环周期的最后一位数字是d，则有一件小事我们可以肯定，就是乘积nd的结束数字为9。这是必然的，只有这样才能使得除法在这一步骤时的减法得到1，从而开始下一个循环。例如，对1/11，d= 9；对1/7， d=7；1/3，d=3；如此等等。

五度相生律

物理学证明，如果乐音的主频率之间是简单的比例关系，那么它们配合在一起时听起来就让人感觉到和谐、悦耳。虽然古人没有声波及其频率的概念，但他们也摸索着发现了乐音之间“简单比例”的规律。

毕达哥拉斯发现，如果一根长度给定的弦发出的乐音是do，那么，其一半长度的弦发出的乐音就是比do“高八度”的“高音do”。也就是说，八度音程的同名唱音之间的频率比是2∶1，频率越高，声音越高。

毕达哥拉斯还发现，弦长比例为3∶2时的两个乐音之间的声音非常和谐，因此他将这个比例之间的音程定为五度音程。换句话说，do与so的弦长比例被毕达哥拉斯确定为3∶2。换成频率，就是发出do的频率是so的频率的2/3。

于是，毕达哥拉斯用这样的办法来确定音阶：（1）首先规定do的弦长。（2）用do弦长的2/3，确定出与它距离为五度音程的so。（3）用do的3/2倍弦长确定它的下方五度，即低音fa；再用低音fa的一半弦长产生fa。

（4）用so的2/3弦长确定其上方五度，即高音re；用高音re的两倍弦长确定re。（5） re2/3用弦长的确定它的上方五度，即la。（6）用la弦长的2/3确定它的上方五度，即高音mi；然后，用这个弦长的2倍确定mi。（7）用mi弦长的2/3倍确定它的上方五度，即si。于是

循环小数与由连续n个9构成的数紧密相关，因此也与由连续n个1构成的数有紧密的联系。由连续n个1构成的数是否是素数？这是个有趣而且也有意义的问题。事实上我们不难证明，由连续n个1构成的数如果是素数，那么n必然是素数。但反之不然。例如11是素数，但111不是。

现在，我们面前至少出现两个趣味问题：（a）由连续n个1构成的数中有多少是素数？（b）如何找出这些数？遗憾的是，两个问题的答案目前都还不知道，而第二个还很有可能是一个我们永远找不到答案的问题。

在11之后，接下来的四个由一串1构成的素数分别有19个1、23个1、317个1，以及1031个1。第六个是什么？我们还不确切地知道。目前为止，我们知道1的个数为49081个、86453个、109297个、270343个的四个数很有可能是素数，但还没有确凿的证明。而除了以上五个素数和四个疑似素数之外，在n<2500000时的其他由n个1构成的数都是合数。我们不知道总共有多少这种形式的素数，但猜想它们有无穷多个。

以上说的是十进制数的情况。回想等比数列的求和公式，十进制中由连续n个1构成的数即

相似地，如果使用二进制，则由连续n个1构成的二进制数等于2ⁿ-1。我们在第2章讨论过，这种数如果是素数，那么它一定就是梅森素数。因此，由连续n个1构成的二进制数中，我们已经知道有49个是素数。

我们来考虑这样一种情形：k是一个大于1的数，p₁， p₂，…，p_n是不同的素数，并且它们的循环周期都有k个数字。我们从前面的讨论中可以看到，这意味着它们都整除10^k-1，即由k个9构成的数。但是9也整除10^k-1，所得的商由k个1构成。因此，如果p₁，p₂，…，p_n是所有循环周期为k的素数，则它们的乘积为

即恰由k个1构成的数。因此，两个问题是相同的：如果我们知道所有素数的循环周期，则我们至少已经部分地解决了（a）和（b）。

对这个问题的研究没有得到什么惊人的成绩，但对它的反问题的研究则成果颇丰。假如我们问，有多少素数的循环周期是7？这需要我们寻找整除9999999的素数。这看似是需要测试所有之前的素数那样可怕的问题，但事实上这样的素数必须整除1111111。如果我们机缘凑巧知道1 111 111的素分解为239×4 649，那我们非常幸运。这说明239和4649是仅有的两个循环周期的长度等于7的素数。此前我们注意到：1 / 11的循环周期长度为2，是其最大可能周期10的真因子。我们必须避免类似情况的困扰，因此目前将讨论范围限制在最大可能周期长度为素数的情形。此时我们有如下定理：

定理：令q为一个周期长度，并假设q为大于3的素数。则所有循环周期长度为q的素数之乘积等于由一串共q个1构成的自然数。反之，q个1构成的数的素因数是仅有的周期长度为q的素数。

高斯在19岁的时候对这个问题产生兴趣，他计算了1000以内的所有素数倒数的小数展开式。然而，1000远远不是一个足以停止计算的大数。下面的表格中列出了所有周期长度小于21的素数，其中有一处需要计算到10亿以上。

这个列表最让人惊讶的地方是循环周期短小的素数之稀少——我们原以为表中很多行都会有数以百计的素数，事实上却只有一个、两个，或三个。

讨论完连续一串1构成的数之后，我们来考察一种连续一串根号的表达式，即无穷的、看起来有些奇怪的根式迭代式：

我们的问题是：是否存在n使得此式的极限为整数？乍一看肯定的答案似乎是相当不可能的。确实，如果它有极限，该极限看似必然会是一个无理数。然而，答案不仅是肯定的，而且对合适的n，这个根式迭代式可以逼近任意大于1的整数，所需的n还可以非常容易地求出来。

我们用递推公式来定义一个数列{x_n}，它满足：

用数学归纳法不难证明，这个数列是递增的，并且它的每一项都小于n+1。因此根据前面我们提到的“单调有界原理”，数列{x_n}是有极限的。当然，这个极限就是我们这里的奇怪根式的值。如果我们假设数列{x_n}的极限为x，则从数列的递推定义式我们可以得到：

两边同时平方，即有

或

n=x（x-1）。

如果x是整数，则x-1也是，因而我们得到了简单的求解整数n的公式。例如，对x=2，我们得到n= 2；对x= 3，则有n=6。就是说，我们立刻得到如下有趣的等式：

单调有界原理

又称“单调有界准则”或“单调有界定理”，它陈述的是关于数列的这样一个性质：如果一个数列是单调递增的，并且有上界，那么它就一定有极限。相似地，单调递减且有下界的数列也有极限。

如果数列的通项a_n随着n的增加而增加，那么这个数列就是“单调递增”的。也就是说，如果对任何自然数n，总有a_n+1≥a_n，那么我们就说数列{a_n}是单调递增的。如上所述，“单调递增”通常的意思只是“不减”，即a_n+1≥a_n。如果数列满足a_n+1>a_n，则通常称之为“严格递增”。

如果存在一个数M，使得对任何自然数n，都有a_n<M成立，那么我们就说数列{a_n}有“上界”，而M就是它的一个上界。很显然地，如果M是{a_n}的上界，那么任何比M大的数也都是该数列的上界。

单调有界原理是关于数列极限问题最重要的定理之一，它可以用来判断数列是否有极限，但并不给出具体的极限值。

例如，考虑这样一个数列{a_n}：它的第一项a₁= 1，而此后的通项由递推公式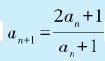定义。

由于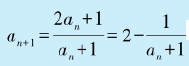，用归纳法不难证明数列是单调递增的。此外，2显然是数列的一个上界。因此，由单调有界原理，这个数列有极限。

一串无穷的根式我们用数列极限的形式解读了它的涵义。那么，像2²这样奇怪的表达式有意义吗？如果我们令x=2²，那么根据对数运算公式，就有

这个等式右边是可以计算的，我们可以从对数表中得到x的“值”。然而，对数表中的那个数其实只是近似值，因此， 2²究竟是什么样的数？我们又怎么计算出对数表里更精确的数值？这些都是值得思考的问题。

我们首先应该回忆一下像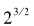这样的表达式的意义。如果从幂和根的角度考虑这个数，那么我们知道：

这是一个我们熟悉的数字。然而，与3/2很不一样，它不能表示成分数，因此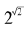也不能像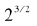那样化成一个根式。也就是说，这个回忆还没有回答我们关心的问题。

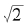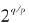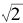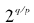然而我们前面介绍过，可以用一个分数的数列来逼近。相似地，以为极限的分数数列也是存在的。对分数数列的每一项q/ p，我们刚刚的回忆告诉我们：都是有意义的。因此，表达式也就有确切的意义了，它应该被定义为当q/ p逼近时的极限。

我们无法凭观察确定哪个无理数次幂的值会是有理数，因此我们无法简单地判断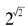是不是有理数。然而我们不难证明：存在某些形如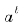的表达式，其中的a与b都是无理数，但a的b次幂的结果却是有理数。

考虑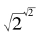，我们不知道它是不是有理数。但这没有关系，它要么是有理数，要么是无理数，二者必居其一。如果它是有理数，则我们得到a=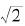，b=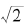两个无理数，但a的b次幂是有理数。

如果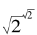是无理数，则我们将它记为a，然后取b=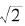作为次幂。这样，按照指数的运算法则，我们得到：

这不仅是有理数，而且还是整数！

事实上，以上的第二个可能性是正确的。经过很多数学家的长期努力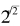，终于被证明是一个超越数。回顾我们给出的超越数的定义，这意思是说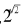，不是任何代数方程的根。

最后，我们再做点有趣的运算：

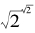由于是一个超越数，上述运算表明，也只能是一个超越数，而上一段落中定义的x则是一个超越数的无理数次幂结果为一个整数的例子。

阿基米德

阿基米德（约前287—约前212）是古希腊数学家、物理学家、发明家、工程师、和天文学家。他出生于西西里岛的锡拉库扎（又译“叙拉古”），第二次布匿战争时，阿基米德死于围攻锡拉库扎的罗马士兵之手。

阿基米德无疑是古希腊最杰出的科学家，他对数学和物理学的影响都极为深远，经常被视为与牛顿和高斯等并列的、有史以来最伟大的数学家。

阿基米德发现浮力原理里，兴奋地大喊“ευ'ρηκα（我发现了）！”这个词从此成为西方文化中非常著名的感叹词，英语拼写为Eureka。

阿基米德对圆及一般圆锥曲线、球和圆柱等各种立体都有非常深入的研究。他用割圆术计算圆内接与外切正96边形的边长，得到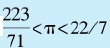的结果。他的方法与刘徽在为《九章算术》作注时所用的方法一样，但比刘徽早400多年。此外，阿基米德用微积分的思想，推算出圆的表面积和体积公式，比祖冲之父子早大约700年之多。

阿基米德对球体积公式的证明

阿基米德的证明采用物理学的表述形式，如果改用数学的表现方式，则他的证明是这样的：

图一

图二

图三

图四

如上诸图所示意，以2R为底半径及高作圆锥，以R为半径作球，以旋转体视之，旋转之前的截面如第一图所示，二旋转体如图二、图三所示。在距离锥顶X处，锥被截出的圆面积为：πX²。据勾股定理，知在此高度处球被截出的圆面积为：

因此，锥的截面积加上球的截面积等于：

2πRX。

而由图四可知，上述这个数值恰好等于图中的卧着的三棱柱在距离顶棱X处的截面积。因此，我们有：

（图三中锥的体积+图二中球的体积）=图四中三棱柱的体积。即：

（图三中锥的体积+图二中球的体积）= 4πR³。

由于锥的体积已知为，所以半径为R的球体积为以上二者之差，即：